基于差分进化算法优化模糊Petri网的电力变压器故障诊断
2019-01-07柳岩妮
王 虎,柳岩妮
(国网潍坊市寒亭区供电公司,山东 潍坊 261100)
0 引言
电力变压器作为电力系统的重要组成设备,其运行的稳定性与电力系统安全性和供电可靠性息息相关。通过对变压器进行故障诊断,有助于及时发现存在问题进行维护,保证电网稳定运行。传统诊断方法采用IEC三比值法[1],随着人工智能方法的引入,神经网络[2-3]、支持向量机[4-6]、故障树[7]以及一些组合方法得到了广泛应用,并取得了不错效果,但在实际应用中存在一定的不足,比如神经网络准确率较低,支持向量机参数优化效率低下等。文献[8]中使用单纯Petri网模型对变压器故障进行诊断,存在诊断效率较低,精度不高的缺点。文献[9]提出的基于BP网络优化模糊Petri网的方法具有很强的推理和自适应能力,但BP算法优化参数收敛速度慢,对诊断效率有很大影响。
模糊Petri网具有模糊推理能力,可以通过网图形式很直观地对系统事件进行建模和仿真。但模糊Petri网自适应和自学习能力较差,其阈值、可信度、权值等参数往往较依赖经验值,导致算法收敛速度慢,精度不高。本文将差分进化算法引入到了模糊Petri网的参数优化中,使用混沌优化初始值,并在优化后期加入了早熟扰动,避免了陷入局部极值。实例仿真表明,该算法收敛速度较快,且诊断准确率较高,具有一定的实用价值。
1 模糊Petri网定义及产生规则
1.1 模糊Petri网定义
定义一个八元组[10]:
FPN={P,T,I,O,M,λ,W,μ}
其中,P={p1,p2,…,pn},T={t1,t2,…,tm}是有限库所集合和有限变迁集合;I(O)是输入(输出)函数,反映变迁到库所的输入(输出)映射关系;M为每一个库所对应的标记值pi∈P(i=1,2,…,n),是一个映射,P→[0,1];λ={λ1,λ2,…,λm}为变迁tj(j=1,2,…,m)的阈值;W={w1,w2,…,wn}表示库所与变迁连接弧上的权值,反应模糊产生规则中前提条件对结论的支持程度;μ={μ1,μ2,…,μm}为变迁tj(j=1,2,…,m)的可信度值。
1.2 模糊推理规则
定义S型函数:
y(x)=1/(1+e-b(x-k))
(1)
当b为足够大的常数时,若x>k,e-b(x-k)≈0,则y(x)≈1;若x 定义变迁点燃连续函数: z(x)=y(x)×μ(ti)×x (2) 若y(x)≈1,则z(x)=μi×x>0表示变迁点燃输出对应库所的标记值;若y(x)≈0,z(x)=0表示变迁未点燃,输出库所的标记值保持不变。 差分进化是一种模拟生物进化的随机模型,采用实数编码,主要包括变异、交叉、选择3个操作过程。其具体优化步骤如下[11-13]: 初始化:设置种群规模为N,维数为D,变异常数F为[0,2]上的一个实常数,交叉概率为CR,初始化种群为X0=[X10,X20,…,XD0]; 变异:选择父代中3个不同的个体Xr1G,Xr2G,Xr3G按照式(3)进行差分变异操作,产生新个体ViG+1。 (3) 其中,r1,r2,r3∈{1,2,…,N},且i≠r1≠r2≠r3。 交叉:为使种群具有多样性,对变异后新产生个体ViG+1按照式(4)进行交叉,并交换新旧群体的部分个体,生成新个体UiG+1。 (4) 其中,j=1,2,…,D,rand(j)为[0,1]之间的均匀分布概率,k为[1,D]之间的随机整数。 选择:使用“贪婪搜索”策略进行个体选择。将交叉后产生的新个体UiG+1与初始个体XiG的适应度值f(x)进行比较。如式(5)所示,若前者优于后者,则在第G+1代中用UiG+1取代XiG;反之,XiG不变。 (5) 为了避免差分算法后期陷入局部收敛,初始种群的选择和如何判断种群是否陷入局部收敛是非常重要的问题。本文采用混沌算法对初始种群进行优化,并在种群进化后期加入了早熟判断和处理机制,具体方法如下: 采用混沌算法式(6)[14]对初始种群进行优化。 y(t+1)=χy(t)(1-y(t)) (6) 随着迭代次数的增加,收敛后期容易出现“聚集现象”。本文引入了早熟判断和处理机制。设定群体的适应度方差[15]为: (7) 其中,fi为第i个粒子的适应度值,fv为当前所有粒子适应度值的平均值。为使|(fi-fv)/f|的取值在[0,1]之间,引入了归一化因子f。 取适应度方差定值为ε,适应度精度为fep。若连续N0代满足式(8)则算法陷入局部最优。 (8) 如果算法陷入局部最优,则根据当前种群迭代次数G与最大迭代次数Gm按照式(9)重新调整变异因子FG,从而使其跳出局部最优。 FG=FG×2e1+2/(gm-g) (9) 使用改进后的差分算法对模糊Petri网参数进行优化时,要使得权值满足与规则的强制约束条件,即各个输入库所权值相加等于1。所以,在使用差分产生新个体后,应该对新个体按照式(10)对其进行归一化处理,从而权值满足约束条件。 (10) 改进差分优化模糊Petri网参数算法步骤如下: Step1:初始化种群,设定相关参数。设定种群规模为Np,初始变异因子为F0,交叉概率为CR,进化代数为gm。对随机产生的种群个体,采用混沌算法式(6)对其进行优化产生初始种群,按照式(10)对新个体进行归一化处理; Step2:按照2.1中差分进化算法模型依次对种群个体进行变异、交叉、选择,产生新个体; Step3:计算个体适应度值。如果个体的适应度方差和适应度精度值连续N0次满足式(8),则使用式(9)对变异因子进行调整; Step4:判断迭代次数或者适应度精度是否达到设定值,如果满足结束算法;否则,跳转到Step3。 使用优化后的权值参数对收集到的变压器样本数据进行故障预测,分析其准确率。 电力变压器故障[16]主要是由油中特征气体的含量来区分的,主要包括CH4、H2、C2H2、C2H6、C2H45种气体,并将5种气体总和作为总烃。将加上总烃在内的6种气体组分作为模型的输入即Pi1~Pi6,对应专家系统中的命题d1~d6。将变压器故障类型一般过热、严重过热、低能放电、高能放电、局部放电和无故障6种状态作为模型的输出即Po1~Po6,对应专家系统中的命题d7~d12,对应的输出编码值如表1所示。 表1 故障编码值 根据输入输出数据确定最终的FPN模型如图1所示。 由于收集的实验数据波动较大,为加快收敛速度,对其按照式(11)做归一化处理。 yid=1/(1+exp(-xid/Xi)) (11) 其中,Xi为特征气体的注意量。X1代表CH4,X1=50 μL/L;X2代表H2,X2=100 μL/L;X3代表总烃,X3=150 μL/L;X4代表C2H2,X4=3 μL/L;X5代表C2H6,X5=100 μL/L;X6代表C2H4,X6=100 μL/L。 图1 电力变压器故障诊断的FPN结构图 本文将收集的120组数据作为训练样本,90组数据作为测试样本,其中部分样本数据如表2所示。将训练样本数据按照前文介绍的算法步骤进行参数的学习优化。 通过MATLAB编程仿真可得到进化代数与适应度函数误差精度值得曲线如图2所示,进化80代后精度达到10-6左右。对比BP神经网络优化模糊Petri网参数的仿真实验图3,300次迭代后误差精度为10-4。通过图像可以看出差分进化算法收敛速度较快,误差精度准确度更高。 表2 部分样本数据 μL/L 图2 差分进化算法优化参数仿真图 图3 BP神经网络算法优化仿真图 将差分进化算法优化得到的参数作为模糊Petri网的对应参数,对收集的变压器数据输入FPN结构进行故障诊断。经过多次训练调整达到最优网络结构后,将如表3所示的测试样本组成数据输入到FPN结构中,得到测试样本的故障诊断结果。 表3 测试样本组成 为验证差分进化算法优化模糊Petri网的诊断结果准确率,本文分别使用未经优化的模糊Petri和BP神经网络优化的模糊Petri对收集的数据进行训练和测试,并进行对比。3种算法的诊断结果如表4所示。 表4 3种算法诊断结果对比表 通过表4中诊断结果数据分析可得,本文提出的差分进化算法优化模糊Petri网的方法故障诊断准确率为81.73%,对比未经处理的模糊Petri网和BP神经网络优化模糊Petri网两种方法的准确率74.21%、77.46%,分别提高了10.13%、5.51%,从而表明了本文算法故障诊断准确性较高,具有一定的可行性和有效性。 (1)构建的差分算法优化模糊Petri网模型适用于电力变压器故障诊断,测试故障预测准确率达81.73%,能较为准确地对多类故障进行诊断。 (2)通过MATLAB仿真图可得,改进的差分算法优化模糊Petri网参数与BP神经网络相比,收敛速度更快,全局性更强。 (3)将算法应用到工程实例,结果表明,优化后的网络模型对变压器故障诊断准确率更高,具有一定的实用价值。2 差分进化算法
2.1 差分进化算法的模型
2.2 差分进化算法的改进

3 改进差分算法优化模糊Petri网参数
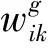
4 实例分析
4.1 诊断模型建立


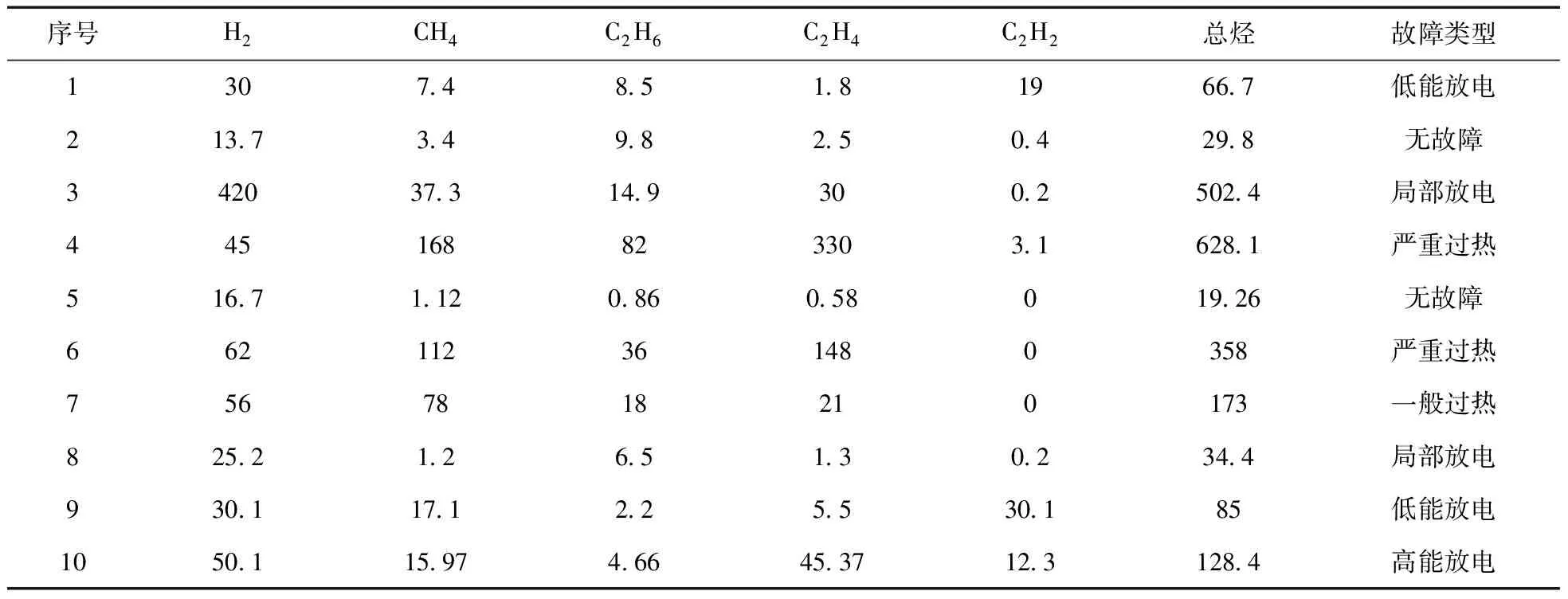
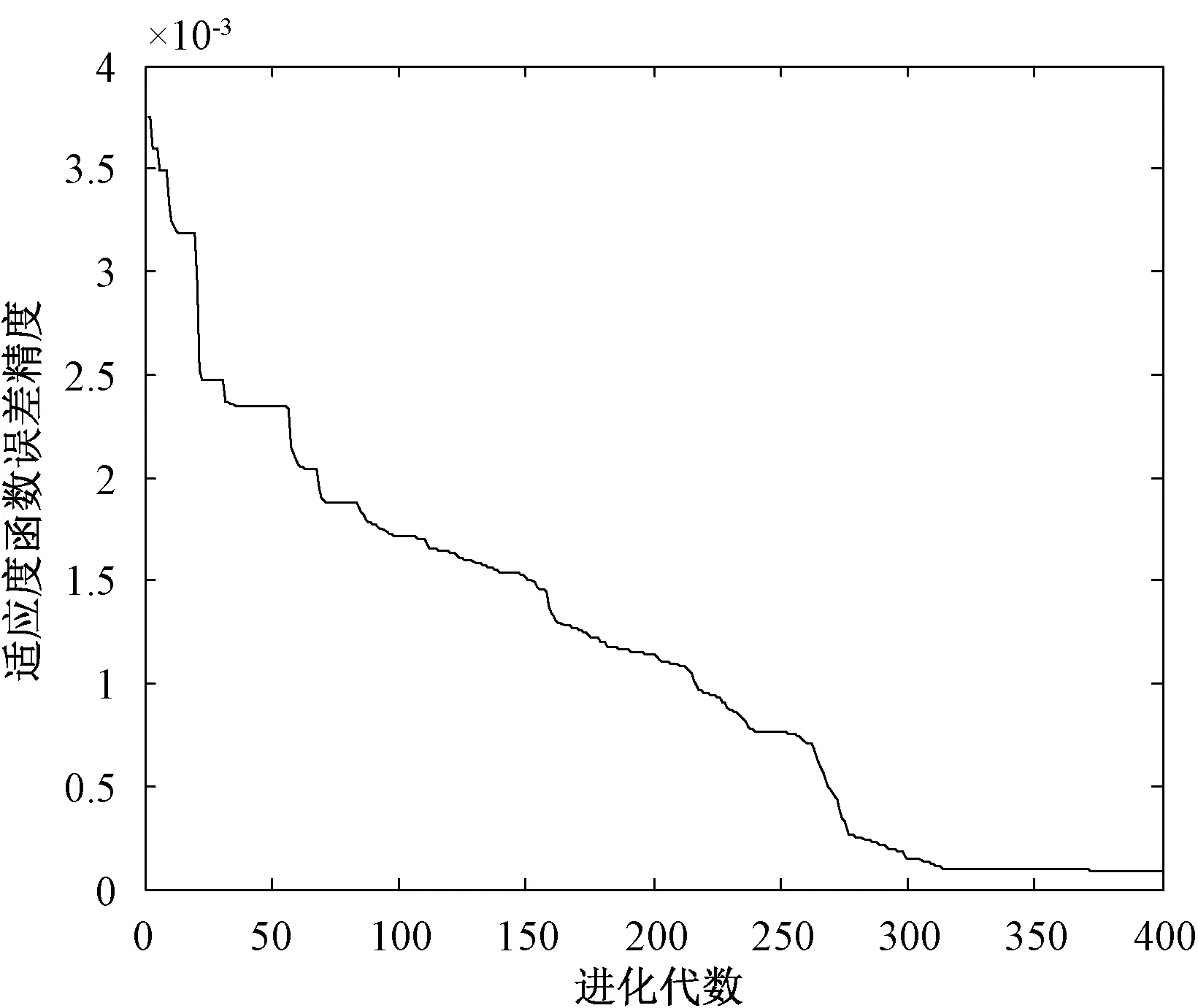
4.2 实例仿真


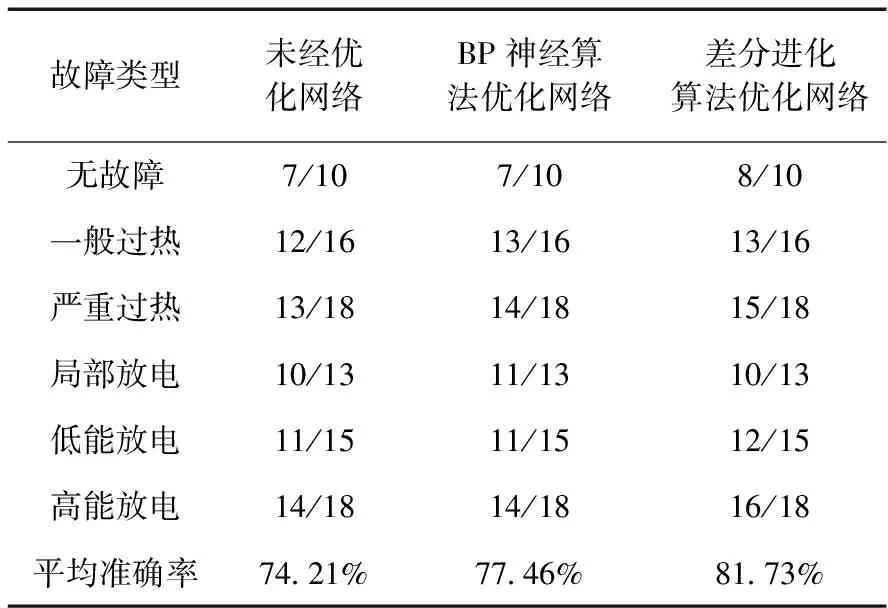
5 结论
