一种基于k-means的两阶段用电异常检测方法

张铁峰，张 靖

(华北电力大学 电气与电子工程学院，河北 保定 071003)

0 引言

随着智能配电网和高级量测体系的不断发展，配用电数据逐渐呈现出体量大、类型多、增速快等大数据特征[1]。但是受设备故障、通信故障、电网波动和用电管理等因素的影响，这些数据中包含大量异常的用电数据[2,3]。在智能配电网中，利用有效的异常检测方法可以及时监测到用电异常故障情况，从而进行处理，减小企业的非技术损失[4]。因此，用电异常检测对于提高电力服务水平，减少电网的非技术性损失(non-technical losses,NTLs)，节约大量人力资源以及降低运营成本有着重要意义[5]。

由于电能的不可大量存储特性，传统的用电异常检测一直都是以反窃电技术为主，从源头上防止异常用电，然后以现场检测为辅进行的。传统的异常用电检测有定期巡检、定期校验电表、用户举报窃电等方法来发现窃电或计量装置故障等[6,7]。这些方法存在耗费人力物力大，误报多，耗时长，效率低的问题，同时，也难以发现用电异常背后的关联事件信息。因此，需要开发新的用电异常检测方法。

当前，国内外研究人员针对用电异常检测提出多种不同方法。文献[8]提出一种基于密度聚类技术的用电异常检测算法，根据基于密度的聚类技术，将局部离群点转化为异常用电波动区间的离群度，利用关联分析法构造关联规则，同时给出关联规则支持度，结合当前用电量总和来分析获取异常用电的得分，从而进行用电异常检测。文献[9]提出一种基于人工神经网络的用电异常检测方法，首先搭建了用于处理海量用电数据的分布式存储Hadoop平台，选取了总电能示值、电能峰值、电能谷值、电压电流、功率因数等12个用电数据指标，然后分析和改进了适用于并行处理的BP神经网络算法，进而提出了基于人工神经网络的用电异常嫌疑分析模型。文献[10]提出LOF和支持向量机相结合的异常判别方法，根据各节点LOF值的大小实现智能配电网异常定位，然后对电压进行小波变换，以三相电压的小波奇异熵值建立异常特征样本库进行预分类，并以此为基础建立SVM异常类型判别预测模型。综合国内外研究现状，目前对用电异常检测的分析研究存在以下不足：

(1)局部离群因子算法的时间复杂度高，参数的设置对用户的依赖性比较强，并且算法的可伸缩性较差[11]。

(2)基于神经网络方法的异常识别模型存在着以下的缺点：神经网络高度依赖网络的训练过程，所选择待测数据及其代表性将直接关系到最终所得到的检测结果；检测过程中需要选择适当的阈值，以便比较得到结果，而阈值的选择具有主观性；容易出现残差淹没和残差污染，从而造成漏检和误检[12]。

(3)基于支持向量机的异常识别模型不适用于大规模训练样本，且对多分类问题的解决也存在困难[12]。

k-means聚类算法由于其算法复杂度低、速度快的优点常用于电力负荷模式的提取，以满足电网与用户交互的处理时间要求[13,14]。基于此，本文提出一种基于k-means聚类算法的两阶段异常检测方法。同时，方法考虑了影响电力负荷变化的温湿度影响并修正[15,16]，而季节、节假日、工作日与周末则在负荷模式提取时加以考虑。

首先选取用户用电负荷历史曲线进行k-means聚类以提取其典型负荷模式，然后用灰色关联分析确定影响负荷变化的温度和湿度因素以获得典型负荷曲线的修正系数，再以两种不同的方法将待测日曲线和典型负荷曲线进行比较，给出用电异常嫌疑用户列表供用电稽查参考，两种不同比较方法的互校验验证了方法的有效性。选取山东某酒店的实际用电数据进行分析，与稽查结果对比表明，该方法具有较高的异常检测准确率，在电力用户的用电异常检测方面具有应用前景。

1 基于k-means聚类算法的用电异常检测方法

该方法流程如图1所示。

图1 基于k-means聚类算法的用电异常检测流程

其步骤如下：

(1)数据选择。从用电终端获取用户用电负荷数据，包括某地温度、湿度以及相对应时刻的电力用户负荷数据。

(2)数据预处理。通过用电终端获得的数据可能有缺失值，同时需要将文本型数据进行量化处理以及对数据进行规范化处理。

(3)关联性分析。电力负荷受到诸多非线性因素影响，用灰色关联分析法确定影响负荷变化的关键因素以及对负荷结果的影响程度。

(4)负荷模式提取。采用k-means聚类算法提取用户典型负荷曲线。季节、节假日、工作日与周末在此步骤考虑。得到待测数据中和聚类后与典型负荷曲线距离最小的那一类数据，将他们和对应的温度、湿度数据提取出来。

(5)修正系数。利用灰色关联分析法确定负荷影响因素，获取典型负荷曲线温湿度修正系数。

(6)用电异常检测。将待测日负荷曲线和修正的典型负荷曲线进行比较，按相似度距离大小提供嫌疑用户列表，供用电稽查参考。

2 基于k-means聚类算法的用电异常检测基础

k-means算法是一种基于划分的聚类方法，由J.B.MacQueen于1967年提出。它以k为参数，把n个对象分为k个簇，以使簇内具有较高的相似度，而簇间的相似度则较低。相似度的计算根据簇的质心(一个簇中对象的平均值)来进行[17]。

2.1 k-means算法原理

输入：参数k，数据集N(n个对象)

输出：k个簇Ck

步骤1：任意选择k个对象{w1,w2,…,wk}作为初始聚类中心，其中wj=xi，j∈{1,2,…,k},i={1,2,…,n}；

步骤2：计算每个样本与簇Cj的聚类中心xCj的距离d(xi,xCj)，i=(1,2,…,n/s)，j∈{1,2,…,k}，若d(xi,xCj)=min{d(xi,xCj),j=1,2,…,k}，则xi∈Cj；

步骤3：更新簇的平均值即聚类中心；

步骤 5：若E值收敛，则算法终止；否则返回步骤2。

2.2 关联因素分析与修正系数的获取

2.2.1 灰色关联分析

灰色关联分析方法是基于灰色系统理论而形成的一种数据分析方法，对于两个系统之间的因素，其随时间或不同对象而变化的关联性大小的量度，称为关联度[18]。

将反映系统数据特征数据序列作为参考序列，将对系统产生影响组成的数列{x1,x2,…,xp}，作为比较数列。设有p个比较数列，参考数列为x0，参考数列与比较数列的影响因子ξi(s)由下列公式给出：

ξl(k)=

(1)

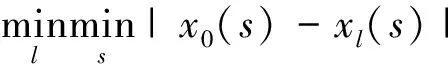
由于比较数列和参考数列在N个点都对应一个关联系数，故取其平均值，得到最终关联度为：

(2)

2.2.2 温度修正

采用k-means聚类算法提取用户典型负荷曲线，得到待测数据中和聚类后与典型负荷曲线距离最小的那一类数据，将他们和对应的温度、湿度数据提取出来进行研究，分析负荷与其对应温湿度的关系。

通过关联性分析可知，负荷与温度存在正相关性，二者之间存在线性关系。设负荷为L，温度为T。

通过实验测定和理论推算，最宜人的室内温湿度是：冬天温度为18～25 ℃，湿度为30%～80%；夏天温度为23～28 ℃，湿度为30%～60%[19]。基于此，在探究负荷与温度关系时控制日平均湿度为30%～60%，即认为在此湿度范围内可忽略湿度对负荷的影响。

因此，通过实验计算得到温度修正模型如下：

(3)

式中：α为负荷和温度的关联度；T为日最高温；LT0为20 ℃时的平均负荷值。

2.2.3 湿度修正

通过关联性分析可知，负荷与湿度存在负相关性，二者之间存在线性关系。设负荷为L，湿度为H。

由标准[19]可知，可在探究负荷与湿度关系时控制日最高温为20～30 ℃，即认为在此温度范围内，负荷主要受湿度的影响。

因此，通过实验得到湿度修正模型如下：

(4)

式中：β为负荷与湿度的关联度；H为日平均湿度；LH0为30%相对湿度时的平均负荷值。

2.3 异常检测模型的建立

设有k种典型负荷模式，m组测试数据，提取的典型负荷模式曲线为Y(y1,y2,…,yk)，经过修正的典型负荷曲线为Z(z1,z2,…,zk)，测试数据为U(u1,u2,…,um)。

2.3.1 模型1

对待测数据U按式(5)进行最大—最小标准化处理，得到经过标准化处理的样本数据V(v1,v2,…,vm)。最大—最小值标准化也叫离差标准化，是对原始数据的线性变换。设u=U(u1,u2,…,um)，建立映射f：

(5)

其中，umax=max(u)=max(u1,u2,…,um)，umin=min(u)=min(u1,u2,…,um)。

按式(6)计算V和Z的欧氏距离。

(6)

分别对Z中每个元素和V各个元素之间的距离进行降序排序，可取所有用户中那些用户典型负荷曲线与其待测曲线距离相差最大的前10个作为嫌疑用户列表。

2.3.2 模型2

对经过修正的典型负荷模式曲线Z进行反标准化处理，得到数据集W(w1,w2,…,wk)，

(7)

其中：wmax=max(w)=max(w1,w2,…,wm)，wmin=min(w)=min(w1,w2,…,wm)。

按式(8)计算U和W的欧氏距离。

d2=

(8)

分别对W中每个元素和U各个元素之间的距离进行降序排序，得到每种典型负荷曲线下与其距离相差最大的前10个样本对应的标号，即为嫌疑用户列表。

3 算例

以山东某电力公司辖区某酒店的日整点负荷数据为例，进行实证分析，筛选具备日期类型数据、气象数据(包括气温相关数据、湿度相关数据等)等属性的有效数据共900条，将分析结果与实际稽查结果对比验证其有效性。在正常数据中随机抽取750条数据作为样本数据，剩余150条作为测试数据。对样本数据和测试数据分别进行存储，测试数据中第120条数据后被证实为异常用电数据。

3.1 数据预处理

对用电终端采集到的数据进行预处理：对于单个点的缺失值，进行剔除工作；对于标识型的数据，利用数值予以替代。

3.1.1 数据标准化处理

采用比较简单的最大—最小标准化处理方法，最大—最小值标准化也叫离差标准化，是对原始数据的线性变换。设x=(x1,x2,…,xm)，建立映射f：

(9)

其中，xmax=max(x)=max(x1,x2,…,xm)，xmin=min(x)=min(x1,x2,…,xm)。按式(9)对负荷数据进行处理，

3.1.2 文本数据量化处理

对于聚类模型而言，所输入的样本数据必须是量化的数据，而日类型、季节属性等都是非结构化数据，需要进行量化处理。

通过对电力负荷数据的分析可知，周一到周五的工作日负荷具有极大的相似性，不同于周六与周日的休息日负荷；同时，节假日、季节对电力负荷也有极大的影响。

将类型属性量化为{工作日，周末节假工作日，周末节假}={1,2,3}，将季节属性量化为{夏，冬，春，秋}={4,3,2,1}。

3.2 典型负荷模式提取

利用k-means聚类算法进行负荷模式提取。由文献[20]可知，选取聚类数为5时聚类效果最佳。该算法通过在迭代过程中不断移动簇集成员，直至得到理想的簇集为止。对电力用户负荷数据进行聚类得到典型负荷曲线，如图2所示。

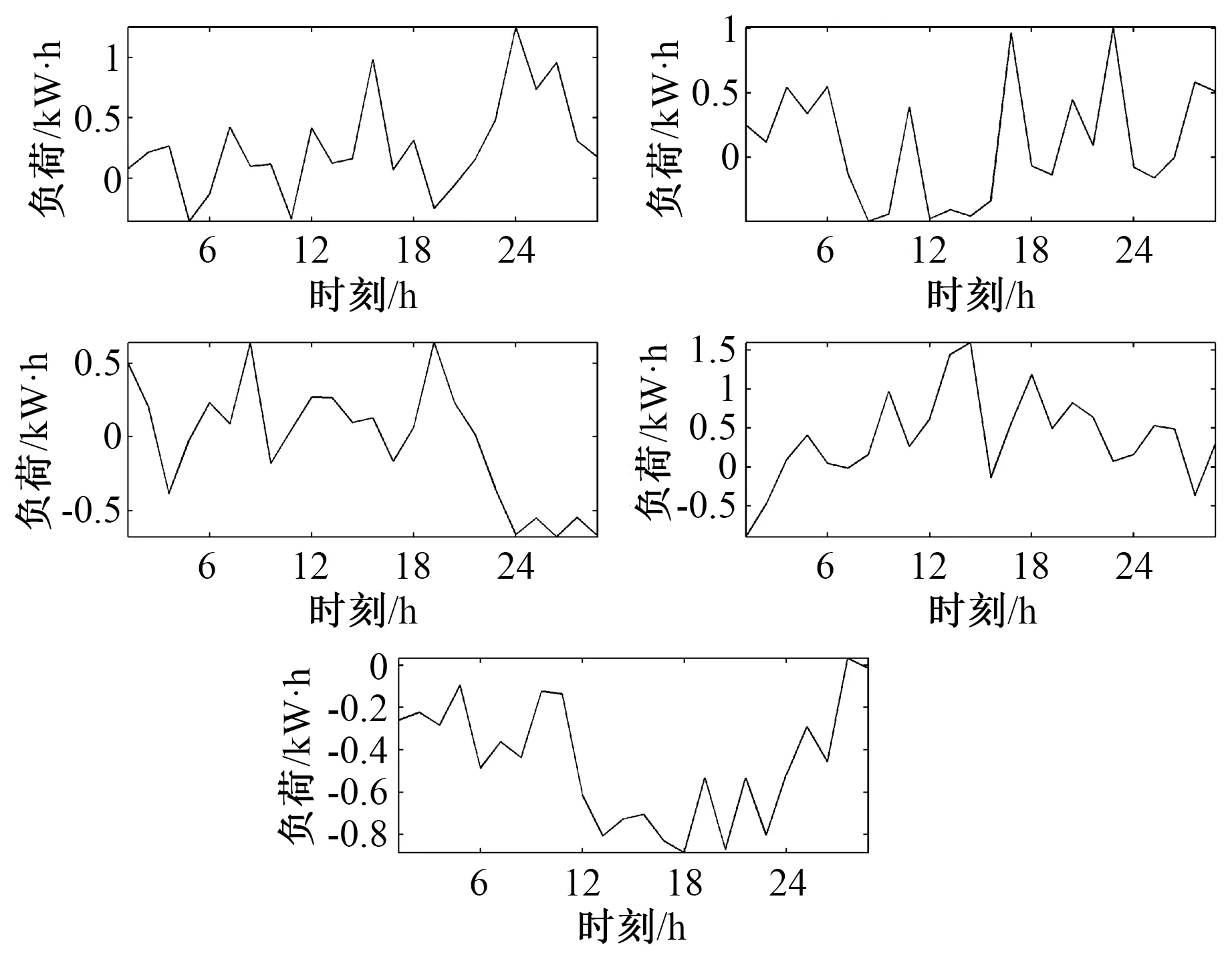
图2 典型负荷曲线

3.3 关联性分析

负荷的外在影响因素分析是指对负荷变化起主导性作用的影响因素与负荷变化曲线之间的相关性分析。灰色关联分析法的优点在于对样本量的多少和有无规律性无硬性要求，并且计算量小，算法简单，可定量分析外在影响因素与负荷变化间的相关程度，非常适合在大数据下进行电力负荷特性分析。

利用灰色关联分析法研究温度、湿度对电力负荷的影响，结果如图3、图4 所示。图中曲线1表示温度曲线或者湿度曲线，曲线2表示负荷曲线，横轴为时刻，纵轴分别为温度或者湿度以及负荷。

图3 温度对电力负荷的影响

图4 湿度对电力负荷的影响

由图3和图4可知，温度与负荷呈正相关性，湿度与负荷呈负相关性，计算得温度与负荷的关联度为0.533，湿度与负荷的关联度为0.427。按2.2.2和2.2.3节所示方法对提取的典型负荷曲线进行预测修正，如图5、图6分别为温度34.5 ℃时以及湿度为52%的预测负荷和实际负荷的对比图。图中曲线1为负荷预测曲线，曲线2为实际负荷曲线。

图5 温度在34.5 ℃时预测值和实际值的对比图

图6 湿度在52%时预测值和实际值的对比图

3.4 用电异常分析

3.4.1 模型1的实现

导入150条测试数据(包括电力负荷数据和对应的温、湿度数据)，对电力负荷数据进行标准化处理，并与经过修正的典型负荷曲线进行比较，分别计算每条负荷曲线和经过修正的典型负荷曲线之间的欧氏距离，并对测试数据和所有模式下的欧氏距离的最小值进行降序排序。取前10名测试数据对应的标号列表显示作为嫌疑用户名单。表1所示为模型1 下的嫌疑用户列表，如表1所示，标号为32、77、88、127、125、120、119、52、62、54的数据与标准负荷曲线差异最大，这几天具有用电异常嫌疑。

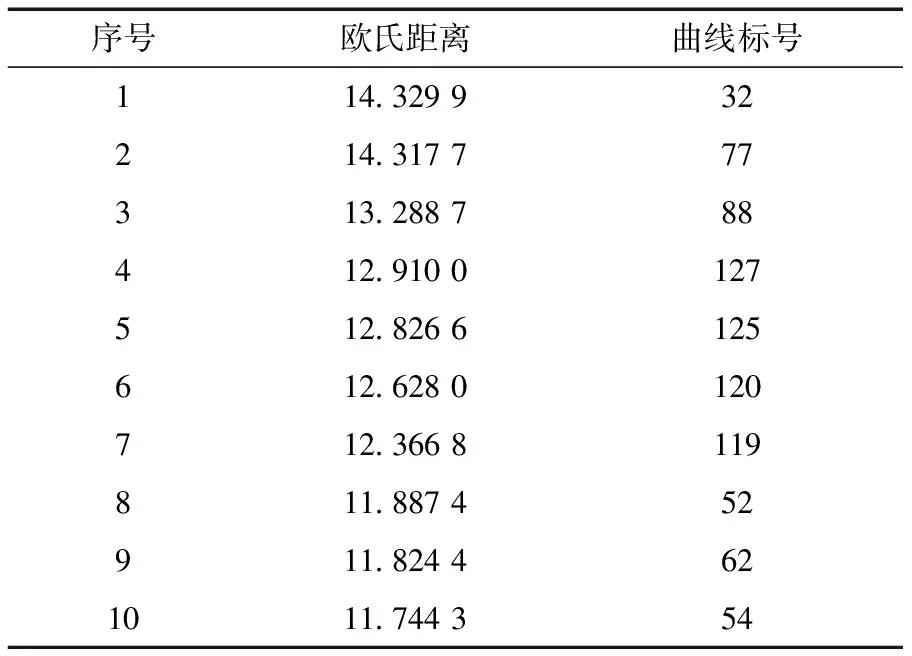
表1 模型1 下的嫌疑用户列表

3.4.2 模型2的实现

导入150条测试数据(包括电力负荷数据和对应的温、湿度数据)，对经过修正的典型负荷曲线进行反标准化处理，并对每条负荷曲线和经过反标准化修正的典型负荷曲线进行比较，分别计算每条负荷曲线和经过反标准化修正的典型负荷曲线之间的欧氏距离，并对测试数据和所有模式下欧氏距离的最小值进行降序排序。取前10名测试数据对应的标号，即为嫌疑用户名单。表2所示为模型2下的嫌疑用户列表，如表2所示，标号为120、119、121、122、147、132、60、47、53、31的数据与标准负荷曲线差异最大，这几天具有用电异常嫌疑。

表2 模型2 下的嫌疑用户列表

对以上用户进行稽查，结果表明，标号为120的用户确实为用电异常用户，证明本文方法有效。

4 结论

针对传统用电异常检测方法耗时长、准确率低、效率低的问题，本文提出一种基于k-means聚类算法的两阶段用电异常检测方法。

主要特点如下：

(1)本文提出的基于k-means聚类算法的异常用电检测方法充分挖掘大数据的价值，利用负荷曲线获取负荷模式检测异常，算例表明其有效性。

(2)所提方法中，采用灰色关联对影响电力负荷的温湿度因素进行关联性分析，对典型负荷模式通过系数进行修正，可以进一步提高检测精度。

(3)为防止标准化过程中的信息丢失产生的影响，采取两种方法对待测数据和经过修正的典型负荷曲线进行比较，经交叉验证，得到可信的用电异常用户嫌疑清单，对于当前用电稽查工作提供了有力的支持，具有推广应用价值。