基于柯西问题的二阶双曲型分布参数系统迭代学习控制
2019-01-07陈小艺
傅 勤,陈 实,陈小艺
(苏州科技大学 数理学院,江苏 苏州 215009)
引言
迭代学习控制由Arimoto等[1]123-140于1984年提出完整的设计方法后, 已成为近年来控制理论研究的热点问题, 并引起研究人员的广泛关注. 在迭代学习控制设计中, 常用的是D型学习律[1]123-140,[2]1177-1182和P型学习律[3]590-600,[4]707-714, 分别适用于非正则系统(系统的输入、输出无直输通道)和正则系统(系统的输入、输出有直输通道).
许多实际问题常用偏微分方程所刻画的分布参数系统模型来描述, 近年来,分布参数系统的应用已经渗透到各个领域, 相应的研究工作也取得了不少成果. 然而, 由于其系统变量涉及无穷维函数空间,至今,将迭代学习方法应用于分布参数系统上的研究成果并不多, 且多集中于抛物型分布参数系统[5]619-623,[6]1082-1085,[7]1155-1163,[8]2397-2408,[9]114-122上. 同时, 涉及双曲型分布参数系统的研究成果[10]284-293,[11]606-611,[12]1086-1089也比较少,文献[10]研究了二阶双曲型分布参数系统的迭代学习控制问题,文献[11][12]则将迭代学习控制方法应用到一阶双曲型分布参数系统系统上.从偏微分方程的定解条件角度来看,文献[5-11]中系统涉及的都是混合问题(既有初始条件, 又有边界条件的定解问题), 涉及柯西问题(只有初始条件的定解问题)的就很少了.文献[12]利用Fourier变换,研究了一类一阶强双曲分布参数系统基于柯西问题的迭代学习控制,在输入、输出有直输通道的情形下,构建得到P型学习律,使得系统的输出跟踪误差于L2空间内沿迭代轴方向收敛.文献[12]在结尾中提出了未来进一步可考虑研究的二阶双曲型分布参数系统的迭代学习控制问题.
本文研究一类分布参数系统基于柯西初值条件的迭代学习控制问题,该系统由二阶双曲型偏微分方程所构建,有一定的不确定性,且输入、输出无直输通道.对分布参数系统的迭代学习控制,通常的处理方法[5]619-623,[6]1082-1085, [7]1155-1163,[8]2397-2408,[9]114-122,[10]284-293,[12]1086-1089是:先在空间方向构建跟踪误差的L2范数, 然后在时间方向上使用λ-范数等常用的一些处理手段,得到跟踪误差在L2意义下的收敛性.本文采用与之不同的处理方法,基于波动方程柯西问题的求解公式[13]7-15,构建得到D型迭代学习控制律.这种借助于求解公式的处理方式, 据笔者所知, 应属首次提出,其不仅简单,而且能使得系统的输出跟踪误差沿迭代轴方向逐点收敛(现有此类问题的收敛均为L2意义下),也毋需涉及到λ-范数等常用的一些处理手段,并且有很大的推广性(许多偏微分方程都是可求得准确解的[13]7-32,49-59).
1 问题描述
考虑如下形式的不确定二阶双曲型分布参数系统:
(1)
这里Q(x,t),u(x,t),y(x,t)∈R分别是系统状态、控制输入、输出;b,c为不确定常数, 满足0<α1≤b≤α2, 0<β1≤c≤β2,其中α1,α2,β1,β2是已知常数. 输出y(x,t)表达式中不含有控制输入u(x,t),即系统输入、输出无直输通道. 对式(1)给出如下假设条件:
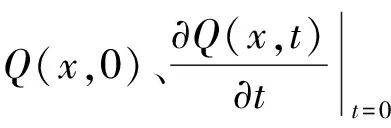
假设2 对于给定的理想轨迹yr(x,t), 存在唯一的控制输入ur(x,t), 使得
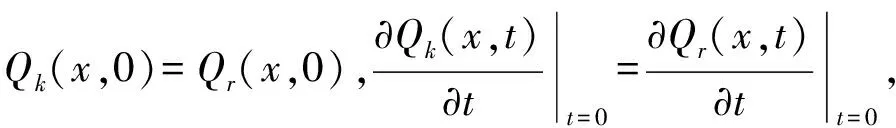
-∞ 设式(1)在有限区间t∈[0,T]内是可重复的, 在迭代学习过程中, 重写式(1)为: (2) 学习控制的目的是寻找适当的学习律, 使得迭代学习序列yk(x,t)逐点一致收敛于理想的输出yr(x,t),即: ∀(x,t)∈(-∞,+∞)×(0,T]. 其中,ek(x,t)=yr(x,t)-yk(x,t). 注1 假设1-3是通常的构建迭代学习控制的假设条件. 引理1 柯西定解问题[13]8-9 的解为: 显然, 将t>0改为0 对式(1)构建D型学习律 (3) 其中,p>0为学习增益,有如下定理: 定理1 假设1-3成立,如果有 (4) 证明记δQk(x,t)=Qk+1(x,t)-Qk(x,t),δuk(x,t)=uk+1(x,t)-uk(x,t),将式(3)改写为: 结合假设3, 有: 应用引理1,得: 即: (5) 由式(2)及假设3,有: 再由引理1及式(5),可得: (6) 由式(2)(6)有: ek+1(x,t)=ek(x,t)+yk(x,t)-yk+1(x,t)=ek(x,t)-cδQk(x,t)= ek(x,t)-cbpek(x,t)=(1-cbp)ek(x,t). 由式(4)可得: |ek+1(x,t)|=|1-cbp||ek(x,t)|≤ρ|ek(x,t)|. (7) 由压缩映象原理可知: ∀(x,t)∈(-∞,+∞)×(0,T]. 证毕. 注3 由式(7)可知, 若选取初始控制u0(x,t),使得e0(x,t)关于x,t是一致有界的,即存在正数M,有: |e0(x,t)|≤M, ∀(x,t)∈(-∞,+∞)×(0,T] 本文研究了一类基于柯西初值条件的分布参数系统迭代学习控制问题, 该系统由二阶双曲型偏微分方程所构建,并具有适定的初值定解条件.同时,提出一种新的处理方式,即在输入、输出无直输通道的情况下,采用D型学习律进行控制设计,得到鲁棒迭代学习控制器,使得系统的输出跟踪误差沿迭代轴方向逐点收敛,取得了很好的效果.2 主要结果
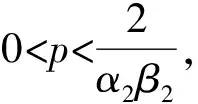
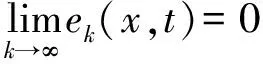
3 结语
