考虑不确定性的电力电量平衡分析

(上海电力学院 电气工程学院, 上海 200090)

电力电量平衡是电力系统调度计划编制的核心,它为电力系统的安全、稳定、经济运行提供了保障[1]。通过预测及保证电力电量的平衡,可以确定未来一段时间电网的基本运行方式,并为设备检修计划、联络线送受电计划、需求侧管理计划、煤炭采购计划以及财务预算计划等制定提供依据。在满足电力电量平衡和电力供应的前提下,能够实现水、火联合发电的经济调度模式,使全网效益最好[2]。为此,电力电量平衡分析一直是研究热点。

文献[3]对逐次切负荷法进行了改进,考虑了电站运行的限制范围,并通过在云南电力系统中的实际应用,验证了所提算法的实用性。文献[4]提出剩余容量日利用小时控制法,解决了电力电量平衡计算中出现的调度被动性和电站之间的不平等性问题。文献[5]构建了考虑电力电量平衡的安全约束经济调度模型,在满足电网安全性与经济性要求的同时兼顾了电力电量平衡的要求。文献[6]利用往年的经验数据,进行了电力电量平衡的分析,总结了中国电力需求与供给增长的历史特征以及电力供需结构的特点。文献[7]根据地区差异,提出华东电网虽然在电力电量平衡方面遇到了困难,但是通过建立电力需求侧管理的长效机制,能够促进电力电量的平衡。文献[8]分析了华东地区的电力电量平衡情况,并针对需求较低的问题进行了重点分析。文献[9]结合华北电网和京津唐的一次能源结构进行了电力电量平衡分析,并提出了经济合理的电源结构建设方案。文献[10]结合历史数据,分析了电力市场环境下的电力电量平衡,并提出了优化运行的方案。文献[11]从电力紧缺的现状出发,提出电力供求的均衡模型和算法。上述文献中电力电量平衡的分析大多基于外部条件已知的前提,缺少了对不确定性运行情况的考虑。

本文以促进电力系统安全稳定经济运行为前提,考虑水火联合发电系统中自然来水与负荷需求的不确定性,建立了以系统总的电力电量缺额最小化为优化目标的电力电量平衡分析模型;同时研究系统约束、机组及机组集合约束、燃煤计划约束、水库用水计划约束等约束条件及其处理方法,并选择高效的求解算法对其进行求解。

1 中长期电力电量平衡分析模型

1.1 目标函数

中长期电力电量平衡分析是以计划期间系统总的电力电量缺额最小化为优化目标,优化计划期内各水火电厂的发电量、燃煤计划和水库水位,因此目标函数为

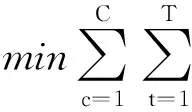
(1)

式中:c——场景编号;

T——时段数目;

ωc——c场景的权重;

α——电量缺额的权重系数;

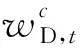
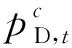
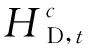
1.2 系统约束

(1) 电量平衡为

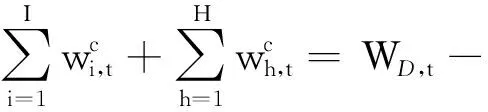
(2)

式中:I——火电机组的数目;

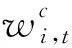
H——水电机组的数目;

WD,t——t时段的需求电量。

(2) 电力平衡为

(3)

PD,t——t时刻的最大负荷;

Rt——t时刻的系统备用。

(3) 火电系统最小和最大发电量约束为

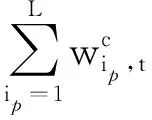
(4)

式中:Wmin,ip,t,Wmax,ip,t——火电系统的最小和最大发电量;

ip——火电厂编号;

L——火电厂总数目。

(4) 水电系统最小和最大发电量约束

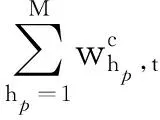
(5)

式中:Wmin,hp,t,Wmax,hp,t——水电系统的最小和最大发电量。

hp——水电厂编号;

M——水电厂总数目。

1.3 机组及机组集合约束

(1) 水电机组出力约束[12]为

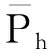
(6)

(7)

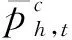
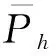
(2) 机组最大发电量(最大可用容量)约束。对单一发电厂,其最大发电量与最大发电功率、负荷率有关。

∀i,∀t,∀c

(8)

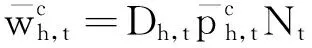
(9)

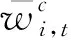
Di,t,Dh,t——水火电机组的有效出力系数,该系数综合考虑了负荷率和强迫停运率;

Nt——t时段的小时数。

(3) 机组最小和最大发电量约束[13]。各机组的发电量应在一定约束范围内进行优化。

(10)

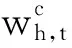
(11)

式中:Wmin,i——火电系统的最小发电量;

Wmin,h——水电系统的最小发电量。

(4) 电厂集合最小和最大发电量约束。对于任一时段,各电厂集合的总发电量应满足上下限约束。

(12)

式中:Wmin,m,t,Wmax,m,t——电厂集合m第t时段的最小和最大发电量;

Mm——水电厂集合m。

1.4 燃煤计划约束

火电厂燃煤库存动态约束[14]和最小燃煤库存约束分别为

(13)

gip,t≥Gip,min

(14)

式中:gip,t——火电厂ip第t时段的燃煤库存;

Gip,t——火电厂ip第t时段的供煤计划;

Fi——煤耗系数;

Gip,min——火电厂ip最小燃煤库存。

1.5 水库用水计划约束

(1) 水库流量约束。发电流量应在其上下限之间。

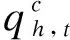
(15)

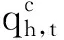
(16)

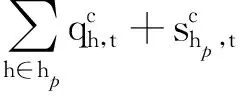
(17)

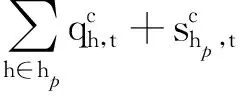
(18)

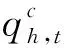
Qmin,h,Qmax,h——发电流量上下限;

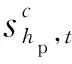
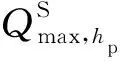
(2) 水库期末库容约束。调度期末,各水电厂应达到预先设定的水位或库容。

∀hp,∀c

(19)

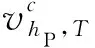
Vterm,hP——设定的调度期末的库容。

(3) 库容约束。各水库的库容应在可调节的范围内变化。

≤Vmax,hp,t∀hp,∀c

(20)

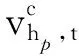
(21)

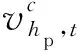
Vmax,hp,t,Vmin,hp,t——第t时段库容的上下限。

(4) 水量平衡约束。对于任意时段,各水库蓄水量应保持动态平衡。

(22)

式中:Δt——时段内包含的小时数;

(5) 水能和电能转换平衡。各水电机组将水能转化为电能。

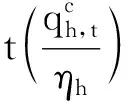
(23)

式中:ηh——第h个水电机组库容下的发电耗水率。

由于上述中长期电力电量平衡分析模型已构建为线性规划模型,因此在GAMS软件平台上调用线性规划算法予以求解。

2 算例分析

测试系统为单场景和多场景,计划周期为2年的中长期调度问题,包含2台火电机组、6台水电机组共8台机组,其中机组的原始数据来自于文献[15]。

2.1 单场景下的电力电量平衡分析

在单一场景下,不考虑缺煤以及水电和火电机组出力的扣减,结合电网的基本数据,对电力电量平衡分析模型进行了仿真分析,得到了以下优化结果。

(1) 电力电量平衡情况。经仿真计算,由于该场景下燃料供应充足,来水情况正常,各时段电力电量缺额均为零,电力系统处于电力电量平衡的状态。

(2) 计划周期内水火电的发电量。对以电力电量缺额最小为目标的仿真模型进行求解,得到满足系统各种发用电约束的可行的水火电计划,如图1所示。火电机组承担主要的发电需求,因而该水火电计划既不节能也不经济,需要进一步进行优化。

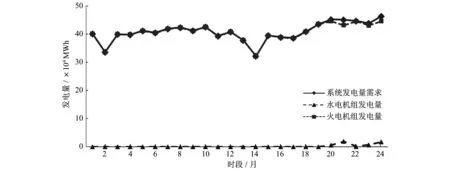
图1 单一场景下各时段水电和火电机组发电量

2.2 多场景下的电力电量平衡分析

考虑了以下4个调度场景,对电网进行计划周期为2年的电力电量平衡分析:中场景是指自然来水、系统最大负荷、系统发电量需求均为计划值;高场景是指自然来水为计划值的110%,系统最大负荷为计划值,系统发电量需求为110%的计划值;中场景1是指自然来水为计划值的90%,系统最大负荷为计划值,系统发电量需求为120%的计划值;高场景1是指自然来水为计划值的120%,系统最大负荷为计划值,系统发电量需求为90%的计划值。

(1) 电力电量平衡情况。经过仿真计算,中场景、高场景、中场景1和高场景1的电力缺额均为零,仅有高场景1的电量缺额为零,其余3个场景均在一些时段存在电量缺额,这说明本文提出的电力电量平衡分析方法能够针对不同的调度场景进行水电和火电发电供需平衡的分析,适应性很强。

(2) 水电和火电机组发电情况。4种场景下水电和火电的计划发电量如图2所示。为了满足发电需求,与中场景相比,高场景下水电和火电的发电量均有所增加,而水电机组和发电量增加更为明显;相比于中场景,中场景1中水电机组的发电量增加幅度较大,而火电机组的发电量与高场景下的火电机组发电量增加幅度相差不多;与中场景比较,高场景1的水电机组和火电机组的发电量均有所减少,水电机组的发电量大多数时段都减小至零。

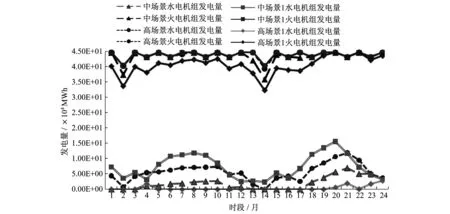
图2 4种场景下的水电和火电计划发电量比较

(3) 火电煤耗量。图3为4种场景下的火电煤耗比较。相比于中场景,高场景和中场景1中火电的发电煤耗量在大多数时段均有所增加,其中第2时段和第14时段增加最多,且中场景1比高场景的增加量更多。

对比中场景,中场景1的发电煤耗量在各时段均有所减少,其中在第13时段和第15时段减少最多。

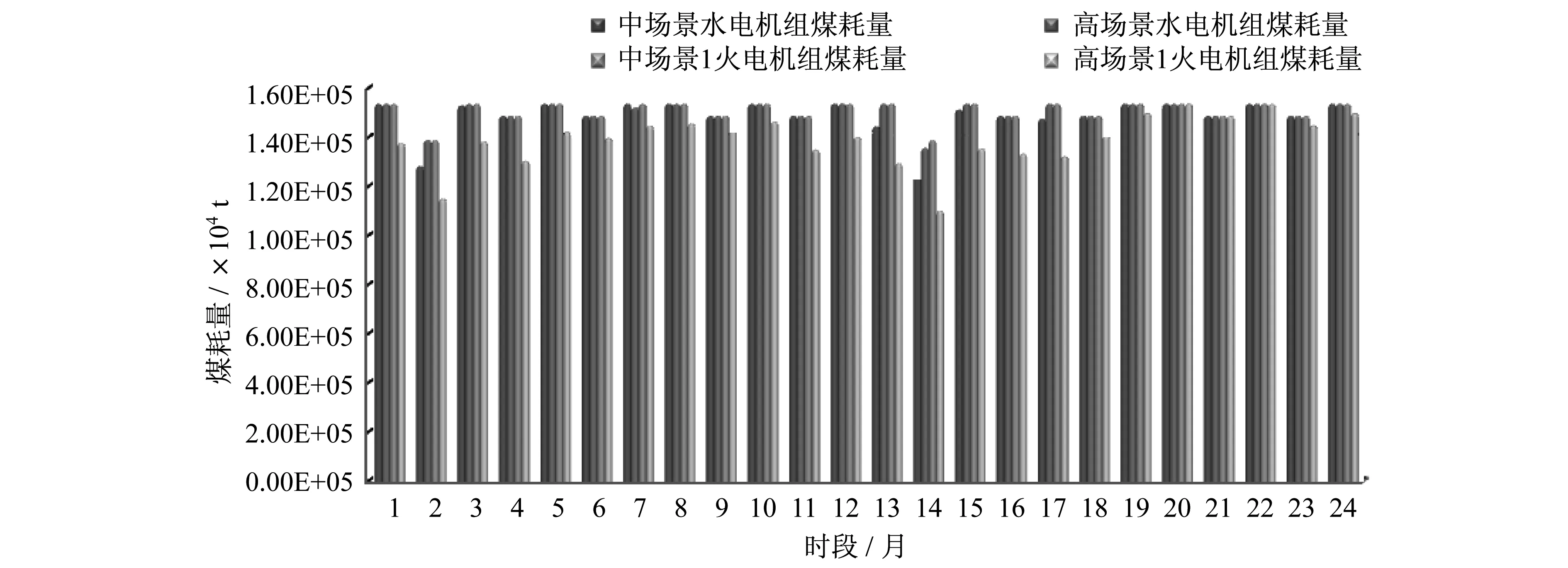
图3 4种场景下的火电煤耗比较

3 结 语

本文针对中长期水火电联合发电计划之间的复杂关系,综合考虑自然来水和负荷需求的不确定性,建立了考虑一次能源不确定性的多场景中长期水火电站联合电力电量平衡分析模型。该模型能够全面优化计划周期内各水火电站的发电量、水库水位和用煤计划。实际算例分析结果表明,水电和负荷的不确定性会影响电力电量平衡的分析结果,需要予以考虑;多场景法能够有效地进行不确定性建模,可以有针对性地开展电力电量平衡分析。