关于树的Wiener维数的一个注记

林 泓，林晓霞，王洪波

(集美大学理学院，福建 厦门 361021)

0 引言

本文所研究的图均为简单连通图。令G是一个连通图，分别以V(G)和E(G)表示G的顶点集与边集，以dG(u,v)表示G的两个顶点u和v的距离。G中的两个顶点的距离的最大值称为G的直径，记为diam(G)。若图G的顶点集可划分为两个子集X和Y，使得G的每条边的2个端点分别在X和Y中，则称G为二部图。连通的无圈图称为树，树中度为1的顶点称为悬挂点。本文其他未加说明的符号和概念参见文献[1]。

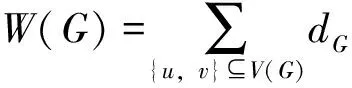
本文以直径为参数得到了树的Wiener维数的一个紧的下界。

1 树的Wiener维数的一个紧的下界

进一步需要以下定义。设T是一个树，以Cd(T)表示T中具有最小距离的顶点的集合[2]。

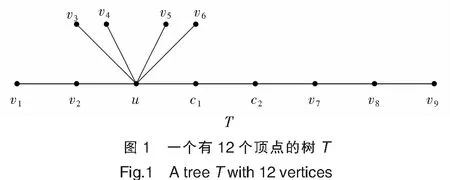
如图1中的树T，容易计算T的12个顶点的顶点距离分别为dT(u)=22,dT(c1)=24,dT(c2)=28,dT(v1)=40,dT(v2)=30,dT(v3)=dT(v4)=dT(v5)=dT(v6)=26,dT(v7)=34,dT(v8)=42，dT(v9)=52。故Cd(T)={u}。

而关于树的最小距离点有引理1和引理2。

引理1[7](Zelinka) 一个树T的质心Cd(T)要么由一个顶点构成，要么由两个相邻的顶点构成。

引理2[2]设P=v1v2…vk是一树T的一条路，其中v1∈Cd(T)，v2∉Cd(T)，vk是树T的一个悬挂点，则有dT(v1)

令x是一个实数，以x表示不超过x的最大整数。本文的主要结论是定理1。

定理1 设T是一个树，则有dimW(T)≥diam(T)/2+1。

证明令diam(T)=r。可假设P=v0v1v2…vr为T的一条最长路，显然v0与vr都是T的悬挂点。令u∈Cd(T)。注意到树T中任意两顶点有唯一一条路相连，故可假设L1是树T中连接u和v0的唯一一条路，而L2是T中连接u与vr的唯一一条路。显然有{V(L1)∪V(L2)}⊇V(P)。否则，若有一点vi∈V(P)(vi≠v0,vi≠vr)且vi∉{V(L1)∪V(L2)}。则T中将有一个包含vi的圈，与T是树矛盾。这样由引理1和引理2可知，L1与L2中至少有一条路中有r/2+1个有不同顶点距离的顶点，故dimW(T)≥diam(T)/2+1。

注1 定理1的下界为紧的。以Pn表示有n个顶点的路，diam(Pn)=n-1,dimW(Pn)=(n-1)/2+1，故dimW(Pn)=diam(Pn)/2+1。

注2 每个树都是二部图，但定理1的结论不能推广到二部图。以Cn表示有n个顶点的圈。C2n(n≥2)是二部图，diam(C2n)=n，而dimW(C2n)=1。若一个连通图G的任意两个顶点间有且仅有唯一一条最短路相连，则称一个图G为测地的。测地图(geodetic graphs)是图的距离理论中常研究的一类图[2]。显然每个树都是测地的，但定理1的结论也不能推广到测地图。C2n+1(n≥1)是测地图，diam(C2n+1)=n，而dimW(C2n+1)=1。