基于多前车信息融合的智能网联车辆跟驰模型
2019-01-06纪艺史昕赵祥模
纪艺 史昕 赵祥模


摘 要:为了进一步提高交通流的稳定性,在经典基于驾驶员记忆的最优速度(OVCM)模型的基础上,提出了一种基于多前车最优速度与紧邻加速度(MHOVA)的智能网联车辆跟驰模型。首先,引入k辆前车的最优速度变化量与紧邻前车的加速度改进OVCM模型,并分别以参数γ和ω表示其权重;然后,结合改进模型利用线性稳定性分析获得交通流的临界稳定条件;最后,利用Matlab对车队施加扰动后的速度和车头距等参数进行数值模拟与分析。仿真结果表明:在车队启动和停止过程的仿真中,所提模型比OVCM模型使得车队整体达到稳定状态的时间更短;在环形道路上车队施加扰动的仿真中,所提模型相比于全速度差(FVD)模型、OVCM和多前车最优速度(MHOV)模型,在合理加速度敏感系数ω和前车数k约束下的速度和车头距波动幅度相对较小,尤其当ω为0.3且k为5时车辆速度的向上和向下波动率最小可达0.67%和0.47%,表明改进模型能较好地吸收交通扰动和增强车队行驶稳定性。
关键词:交通流;跟驰模型;稳定性分析;最优速度;加速度
中图分类号: TP301.6;U491.2文献标志码:A
Car-following model for intelligent connected vehicles based on
multiple headway information fusion
JI Yi, SHI Xin*, ZHAO Xiangmo
(School of Information Engineering, Changan University, Xian Shaanxi 710064, China)
Abstract: In order to further enhance the stability of traffic flow, based on the classical Optimal Velocity Changes with Memory (OVCM) model, a novel car-following model for intelligent connected vehicles based on Multiple Headway Optimal Velocity and Acceleration (MHOVA) was proposed. Firstly, the optimal velocity change of k leading cars was introduced with the weight γ, as well as the acceleration of the nearest leading car was considered with the weight ω. Then, the critical stability conditions of traffic flow were obtained based on the proposed model and by the linear stability analysis. Finally, the numerical simulations and analyses were carried out on the parameters such as velocity and headway of the fleet with disturbance by Matlab. Simulation results show that, in the simulation of the starting and stopping processes of the fleet, the proposed model reduces the time to obtain the stable state of the fleet compared to OVCM does, in the simulation of a disturbance to the fleet on the annular road, if both ω and k are of rationality, the proposed model can perform the less fluctuations in terms of velocity and headway, compared with the Full Velocity Difference (FVD) model, OVCM and the Multiple Headway Optimal Velocity (MHOV) model. Especially when ω is 0.3 and k is 5, the minimum upward and downward fluctuations of vehicle velocity can be 0.67% and 0.47% respectively. Consequently, the proposed model can better absorb traffic disturbance and enhance the driving stability of fleet.
Key words: traffic flow; car-following model; stability analysis; optimal velocity; acceleration
0 引言
車辆跟驰模型是指在车辆编队行驶状态下,利用动力学方法描述后车跟随前车行驶状态的理论,主要以数学模型表达跟驰过程中各种状态参数的演变情况,是交通流仿真的基础理论,对研究通行能力、服务水平、交通流波动具有重要意义。非自由行驶状态下的车辆跟驰具有制约性、延迟性、传递性三个特性。制约性涉及行车速度约束和安全距离约束;延迟性来源于前后车运动状态改变的非同步;传递性体现在前车对后车运行状态的制约呈现依次后传的情形[1]。
国内外相关学者根据车辆跟驰的三大特性开展了大量有关跟驰建模的研究工作[2-4],主要体现在:结合刺激反应理论,Chandler等[5]和Newell[6]分别利用前后车速度差和前后车车间距建立了基于刺激反应的跟驰模型。在Newell[6]所提出模型的基础上,Bando等[7]提出了一种基于前后车车间距的最优速度(Optimal Velocity, OV)模型,该模型具有简单直观和便于数值模拟等优点。Helbing等[8]针对OV模型未考虑前后车速度差所产生的加速度不合理问题,提出了一种广义力(General Force, GF)模型,当跟驰车的速度大于前车时,引入前后车负速度差修正OV模型以避免车辆发生碰撞。Jiang等[9]考虑正负速度差对跟驰车加速度的影响对GF模型进行改进,提出了一种全速度差(Full Velocity Difference, FVD)模型,该模型能更全面地描述交通流的跟驰现象。Peng等[10]引入最优速度关于时间的差值项对FVD模型进行改进,提出了一种基于驾驶员记忆的最优速度(OV Changes with Driving Memory, OVCM)模型,仿真结果表明OVCM模型在交通流稳定性方面优于FVD模型。
综上所述,由于跟驰模型存在的制约性、延时性和传递性,跟驰车在非自由行驶状态下的安全距离、速度、加速度等信息易受到多前车状态的影响。以OVCM模型为例,若前车速度小于跟驰车速度(即两者速度差Δvn(t)<0),车头距Δxn(t)和最优速度V(Δxn(t))将减小,相应地跟驰车的加速度呈现减小趋势;若前车处于加速阶段,在不考虑紧邻前车加速度信息的条件下,需要间接解析前车与跟驰车的速度信息并历经一定的时间延迟才能捕获Δxn(t)的增大趋势,同时在延迟时间段内跟驰车的加速度仍将继续减小。在实际驾驶环境中,如果驾驶员发现前车处于加速状态,跟驰车的加速度不会立即减小,甚至在保证安全车头距的情况下适当地给予增加。因此,充分的多前车状态信息有利于跟驰车得到更加准确的加速度决策信息[11]。
随着车联网技术的发展,跟驰车在智能网联环境中利用车载终端可以有效獲取多前车的状态信息,如车头距、速度、加速度等[12]。本文考虑融合多前车最优速度信息以及紧邻前车加速度信息对车辆跟驰模型进行改进,提出了一种基于多前车最优速度与紧邻加速度的智能网联车辆跟驰(Multiple Headway Optimal Velocity and Acceleration, MHOVA)模型。为了验证MHOVA模型的合理性,首先通过线性稳定性分析获取所提出模型的稳定性临界条件;然后,根据稳定性临界条件设定模型的关键参数,如紧邻前车加速度敏感系数等;最后,利用Matlab仿真平台对车队施加扰动后的速度和车头距等参数的变化规律进行数值模拟,并与FVD、OVCM等模型进行对比分析。
1 MHOVA模型的建立
在车辆行驶过程中,驾驶员根据当前周围车况及道路标识等相关信息做出相应的驾驶决策,这一过程形成了驾驶员的记忆效应[13]。在传统车辆跟驰模型中驾驶员的记忆效应未列入考虑范畴。在实际驾驶环境中,驾驶员对相关交通状态信息存有记忆并会根据所记忆信息调整驾驶行为。文献[10]引入驾驶员记忆效应对FVD模型进行改进,提出了OVCM模型。OVCM模型的车辆运动方程表达式如下:
dvn(t)dt=a[[V(Δxn(t))-vn(t)]+λΔvn(t)+
γ[V(Δxn(t))-V(Δxn(t-τm))](1)
其中:a表示对最优速度的敏感系数;V(Δxn(t))表示跟驰车的最优速度函数;λ表示对前后速度差的敏感系数;τm表示采样时间步长;V(Δxn(t))-V(Δxn(t-τm))表示最优速度在行车时间作用下的差值(记忆效应);γ表示对记忆效应V(Δxn(t))-V(Δxn(t-τm))的敏感系数,当 τm=0或γ=0时,OVCM模型简化为FVD模型。由式(1)可知,如果跟驰车在时间点t的最优速度小于(t-τm)的最优速度,或者跟驰车的最优行驶速度在某一时间段内呈现减小态势,则跟驰车具有减速的倾向,反之跟驰车则具有加速的倾向。
由于多前车速度和紧邻前车加速度对跟驰车的跟驰行为影响较大,引入多前车速度和紧邻前车加速度对OVCM模型进行改进,提出的改进模型MHOVA的运动方程如式(2)所示:
vn(t+T)=V(∑ki=1Δxn+i-1,Δxn-1,Δvn,an+1(t))(2)
式(2)的进一步展开形式如式(3)所示:
V(∑ki=1Δxn+i-1,Δxn-1,Δvn,an+1(t))=aV(Δxn(t))+
λTΔvn(t) +ωTan+1(t)+∑ki=1Tγi[V(Δxn+i-1(t))-
V(Δxn+i-1(t-τm))](3)
其中:T为驾驶员和车辆机械传动等因素产生的延时,表示所期望的速度需要历经时间T才能到达;ω表示跟驰车对紧邻前车加速度信息an+1(t)的敏感系数;k(k≥1)表示所考虑的前车数量总数;γi是代表第i个车关于最优速度记忆的敏感系数;[V(Δxn+i-1(t))-V(Δxn+i-1(t-τm))]表示第n+i-1辆车根据前向观测获得的最优速度记忆,其余项与OVCM模型含义一致。当k=1且ω=0时,MHOVA模型与OVCM模型等价。V(Δxn(t))采用的具体函数如式(4)所示:
V(Δxn(t))=Vmax2[tanh(Δxn(t)-hc)+tanh(hc)](4)
其中:Vmax为车辆的最大速度;hc表示车辆间的安全距离。
式(3)中的延迟时间T不利于公式解析与模型仿真,且加速度对车辆的控制比速度更为直接。因此,对式(3)进行简化,具体过程如式(5)~式(11)所示:
vn(t+T)=vn(t)+Tan(t)(5)
将式(5)代入式(2)得到式(6),进一步得到an(t)的表达式如式(7)所示:
vn(t)+Tan(t)=
V(∑ki=1Δxn+i-1,Δxn-1,Δvn,an+1(t))(6)
an(t)=
1T(V(∑ki=1Δxn+i-1,Δxn-1,Δvn,an+1(t))-vn(t))(7)
取a=1/T,将式(2)代入式(7)得到式(8):
dvn(t)dt=a[V(Δxn(t)-vn(t))]+λΔvn(t)+ωan+1(t)+
∑ki=1γi[V(Δxn+i-1(t))-(Δxn+i-1(t-τm))](8)
为了简化计算,忽略变量Δxn(t-τm)泰勒展开式的非线性项得到简化后的Δxn(t-τm),如式(9)所示:
Δxn(t-τm)=Δxn(t)-τmdΔvn(t)dt=
Δxn(t)-τmΔvn(t)(9)
同理,简化后的V(Δxn(t-τm))如式(10)所示:
V(Δxn(t-τm))=
V(Δxn(t))-τmΔvn(t)V′(Δxn(t))(10)
将式(9)和式(10)代入式(8)得到简化后的运动方程,如式(11)所示:
dvn(t)dt=a[V(Δxn(t))-vn(t)]+λΔvn(t)+
ωan+1(t)+∑ki=1γiτmV′(Δxn+i-1(t))Δvn+i-1(t)(11)
2 线性稳定性分析
若对一个平稳行驶的车队施加一个微小的扰动,如调整中间某辆车的速度,整个车队将脱离原本稳定的运行状态。如果扰动未超出稳定性临界条件,车队经历一定时间后将回归稳定平稳的运行状态;反之,扰动的影响会不断放大,最终使整个车队处于混乱状态。因此,有必要对所提出模型的稳定性进行分析与判定。
利用Lyapunov第一方法并结合线性谐波微扰法[14]分析MHOVA模型的稳定性临界条件。假设车队处于稳定时车头距为h,以最优速度V(h)行驶,每辆车的位置为x(0)n(t)=hn+V(h)t。如果第n辆车在行驶过程中施加扰动项yn(t)=e(ikn+zt),则第n辆车的位置更新后的表达式如式(12)所示,进一步得到yn(t)的表达式如式(13)所示:
xn(t)=x(0)n(t)+yn(t)(12)
yn(t)=xn(t)-x(0)n(t)(13)
对式(13)求一阶导数得到式(14):
dyn(t)dt=dxn(t)dt-V(h)(14)
进一步对式(14)求一阶导数得到式(15):
d2yn(t)dt2=dvn(t)dt(15)
令Δyn(t)=yn+1(t)-yn(t) ,则车头距定义如式(16)所示:
Δxn(t)=h+Δyn(t)(16)
将式(15)和式(16)代入式(11),得到与扰动相关的微分方程如式(17)所示:
d2yn(t)dt2= a[V′(h)Δyn(t)-dyn(t)dt]+
∑ki=1γiτmV′(Δxn+i-1(t))dΔyn+i-1(t)dt+
λdΔyn(t)dt+ωd2yn+1(t)dt2(17)
其中V′(h) = dV(Δ xn)dΔ xn|Δxn=h。
由于yn(t)=e(ikn+zt),令e(ikn+zt)=eM,將式(17)中yn(t)按傅里叶级数展开得到式(18):
z2eM= a[V′(h)(eik-1)eM-zeM]+λz(eik-1)eM+
ωe(M+1)+∑ki=1γiτmV′(h)z(eiki-eik(i-1))eM(18)
将式(18)的参数z按z= z1(ik)+z2(ik)2展开,得到z1和z2的表达式,如式(19)所示:
z1=V′(h)
z2=12V′(h)+1a[λz1-(1-ω)z12+
∑ki=1γiτme(i-1)z1](19)
若z2<0,则车队运行状态不稳定;反之,车队运行状态稳定[15]。根据式(19)中z2的表达式可进一步求出敏感系数a的取值范围,如式(20)所示:
a>[-λV′(h)+(1-ω)V′(h)2-
∑ki=1γiτme(1-i)V′(h)]/V′(h)(20)
考虑5辆前车的最优速度且敏感系数γi按照由近到远依次定义为0.1、0.08、0.06、0.04和0.02,则车头距h与敏感系数a的相位图如图1所示,图中虚线表示稳定性临界曲线,曲线以上部分为稳定区,反之为非稳定区。由图1可得,ω>0时跟驰模型的稳定区大于ω=0时跟驰模型的稳定区,且随着ω的增加,其稳定区逐渐扩大,这表明加入紧邻前车加速度项后能在a的较大取值范围内保持车辆稳定行驶,有利于增强交通流的稳定性。本文提出的MHOVA模型考虑了紧邻前车加速度项(即ω>0),而OVCM模型的ω等于0,从线性稳定性角度而言,MHOVA模型比OVCM模型具有更好的稳定性。
3 数值模拟与分析
3.1 车辆启动与停止过程仿真对比
3.1.1 启动过程数值仿真
本节仿真MHOVA模型在交通信号灯由红灯转向绿灯后车队车辆启动的情况。
车辆启动过程中场景模拟[16]如下:在t<0时,交通信号灯为红灯,车队由10辆车组成,每辆车的位置为xn(0)=(n-1)Δxn,其中n=1, 2, …, 10,车头距Δxn=7.4m,车辆均处于静止状态,即vn(0)=0,n=1, 2, …, 10,车辆的最优速度均为0。t=0时刻,交通信号灯由红色转为绿色,头车开始启动,随后各辆车依次开始启动。最优速度的敏感系数a取值为0.41s-1,前后车速度差敏感系数λ取值为0.6s-1,驾驶员记忆项敏感系数γi取值均为0.1s-1,跟驰车对紧邻前车加速度信息的敏感系数ω取值为0.3,所考虑的前车数k取值为2。选用文献[8]使用实测交通数据标定后的最优速度函数如式(21)所示:
V(Δxn(t))=V1+
V2 tanh[C1(Δxn(t)-lc)-C2](21)
其中: V1=6.75m/s,V2=7.91m/s,C1=0.13m-1,C2=1.57,lc=5m。
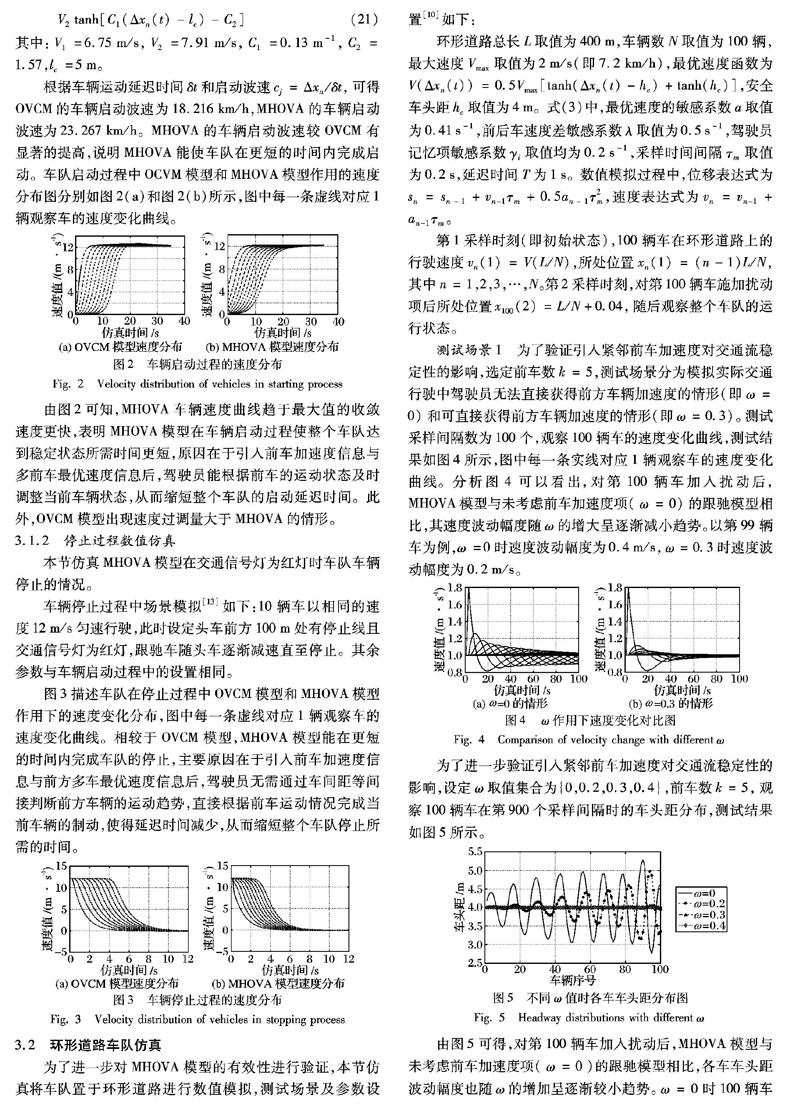
根据车辆运动延迟时间δt和启动波速cj=Δxn/δt,可得OVCM的车辆启动波速为18.216km/h,MHOVA的车辆启动波速为23.267km/h。MHOVA的车辆启动波速较OVCM有显著的提高,说明MHOVA能使车队在更短的时间内完成启动。车队启动过程中OCVM模型和MHOVA模型作用的速度分布图分别如图2(a)和图2(b)所示,图中每一条虚线对应1辆观察车的速度变化曲线。
由图2可知,MHOVA车辆速度曲线趋于最大值的收敛速度更快,表明MHOVA模型在车辆启动过程使整个车队达到稳定状态所需时间更短,原因在于引入前车加速度信息与多前车最优速度信息后,驾驶员能根据前车的运动状态及时调整当前车辆状态,从而缩短整个车队的启动延迟时间。此外,OVCM模型出现速度过调量大于MHOVA的情形。
3.1.2 停止过程数值仿真
本节仿真MHOVA模型在交通信号灯为红灯时车队车辆停止的情况。
车辆停止过程中场景模拟[13]如下:10辆车以相同的速度12m/s匀速行驶,此时设定头车前方100m处有停止线且交通信号灯为红灯,跟驰车随头车逐渐减速直至停止。其余参数与车辆启动过程中的设置相同。
图3描述车队在停止过程中OVCM模型和MHOVA模型作用下的速度变化分布,图中每一条虚线对应1辆观察车的速度变化曲线。相较于OVCM模型,MHOVA模型能在更短的时间内完成车队的停止,主要原因在于引入前车加速度信息与前方多车最优速度信息后,驾驶员无需通过车间距等间接判断前方车辆的运动趋势,直接根据前车运动情况完成当前车辆的制动,使得延迟时间减少,从而缩短整个车队停止所需的时间。
3.2 环形道路车队仿真
为了进一步对MHOVA模型的有效性进行验证,本节仿真将车队置于环形道路进行数值模拟,测试场景及参数设置[10]如下:
环形道路总长L取值为400m,车辆数N取值为100辆,最大速度Vmax取值为2m/s(即7.2km/h),最优速度函数为V(Δxn(t))=0.5Vmax[tanh(Δxn(t)-hc)+tanh(hc)],安全车头距hc取值为4m。式(3)中,最优速度的敏感系数a取值为0.41s-1,前后车速度差敏感系数λ取值为0.5s-1,驾驶员记忆项敏感系数γi取值均为0.2s-1,采样时间间隔τm取值为0.2s,延迟时间T为1s。数值模拟过程中,位移表达式为sn = sn - 1 + vn-1τm + 0.5an - 1τ2m,速度表达式为vn=vn-1+an-1τm。
第1采样时刻(即初始状态),100辆车在环形道路上的行驶速度vn(1)=V(L/N),所处位置xn(1)=(n-1)L/N,其中n=1,2,3,…,N。第2采样时刻,对第100辆车施加扰动项后所处位置x100(2)=L/N+0.04,随后观察整个车队的运行状态。
测试场景1 为了验证引入紧邻前车加速度对交通流稳定性的影响,选定前车数k=5,测试场景分为模拟实际交通行驶中驾驶员无法直接获得前方车辆加速度的情形(即ω=0)和可直接获得前方车辆加速度的情形(即ω=0.3)。測试采样间隔数为100个,观察100辆车的速度变化曲线,测试结果如图4所示,图中每一条实线对应1辆观察车的速度变化曲线。分析图4可以看出,对第100辆车加入扰动后,MHOVA模型与未考虑前车加速度项(ω=0)的跟驰模型相比,其速度波动幅度随ω的增大呈逐渐减小趋势。以第99辆车为例,ω=0时速度波动幅度为0.4m/s,ω=0.3时速度波动幅度为0.2m/s。
为了进一步验证引入紧邻前车加速度对交通流稳定性的影响,设定ω取值集合为{0,0.2,0.3,0.4},前车数k=5,观察100辆车在第900个采样间隔时的车头距分布,测试结果如图5所示。
由图5可得,对第100辆车加入扰动后,MHOVA模型与未考虑前车加速度项(ω=0)的跟驰模型相比,各车车头距波动幅度也随ω的增加呈逐渐较小趋势。ω=0时100辆车的车头距摆动方差为0.4329,ω=0.2时100辆车的车头距摆动方差为0.1128,ω=0.3时100辆车的车头距摆动方差趋近于0。
从图4与图5的测试结果看出,前车加速度项对跟驰车的行驶状态存在直接约束关系,引入前车加速度项的MHOVA模型有利于稳定车速和车头距,从而更有效地促进车队的平稳运行。
测试场景2 为了验证引入多前车最优速度项对交通流稳定性的影响,设定前车加速度敏感系数ω=0.3,测试场景模拟实际交通行驶中驾驶员分别能够获得1辆(k=1)、5辆(k=5)和10辆前车最优速度项的情形(k=10)。采样间隔数为500个,考虑到跟驰模型的传递性和延时性,越邻近施加扰动车辆的跟驰车产生的速度波动影响越大,且第100~51辆车产生的波动大于第50~1辆车,故分别观察第98、80、70和60辆车的速度变化,测试结果如图6所示。由图6可得,前车数k=5时MHOVA模型的车速波动幅度明显低于k=1时的情形;前车数k=10时的MHOVA模型其车速波动幅度反而大于前车数k=5时的情形。由此可得,选取适当的前车数k有利于提高车队的稳定性,与跟驰车距离增大的前车对跟驰车行驶状态的影响逐渐减弱,考虑较大的前车数k反而不利于促进车队行驶的稳定性。
测试场景3 为了验证引入紧邻前车加速度项与多前车最优速度项对交通流稳定性的影响,模拟实际交通行驶中驾驶员可以得到紧邻前车加速度信息和5辆前车最优速度信息的情形(即MHOVA模型),根据图4和图6的数值模拟结果,ω=0.3和k=5时车队整体速度波动达到较小值,故设定前车加速度敏感系数ω=0.3,前车数k取值为5。不考虑紧邻前车加速度的影响,利用5辆前车信息对OVCM模型进行改进可得到多前车最优速度(Multiple Headway Optimal Velocity, MHOV)模型,MHOV模型模拟的实际交通场景为驾驶员可以得到5辆前车最优速度信息的情形。表1~3描述了FVD、OVCM、MHOV和MHOVA四种模型分别在第30、100和500个采样间隔的车辆速度分布情况。参数Vmax、Vave、Vmin、Rup、Rdn分别表示最大速度、平均速度、最小速度、向上波动率与向下波动率。
分析表1~3可得,MHOVA模型在3個采样间隔的上波动率Rup和向下波动率Rdn均小于MHOV模型、OVCM模型和FVD模型;车队加入扰动后随着时间的累积,MHOVA模型的波动率呈逐渐减小趋势,第500个采样间隔时车队车速达到稳定状态,向上波动率Rup与向下波动率Rdn分别为0.67%和0.47%;综上所述,MHOVA模型能较好地吸收扰动且有利于增强车队行驶的稳定性。
4 结语
在智能网联环境中,为了建立更加精准的跟驰模型提升交通流的稳定性,考虑融合多前车行驶状态信息,提出了一种基于多前车最优速度与紧邻加速度的智能网联车辆跟驰(MHOVA)模型。根据线性稳定性分析可得,MHOVA模型的稳定区域大于MHOV模型,且随着加速度敏感系数ω的增加稳定区域不断扩大。数值模拟结果表明:1)在车队启动和停止过程的模拟中,引入紧邻前车加速度项和多前车最优速度信息有利于减少车队整体达到稳定状态的时间;2)确定前车数k时,ω>0时的速度与车头距波动幅度均小于ω=0时的波动幅度,进一步说明引入加速度项有利于增强车队行驶的稳定性;3)确定加速度敏感系数ω时,MHOVA模型选取合理的前车数k有利于提高车队行驶的稳定性;4)选择合理的加速度敏感系数ω和前车数k时,相比FVD、OVCM和MHOV模型,MHOVA模型的速度波动率随着采样时间的增加呈逐渐减小趋势,表明该模型能够有效地促进交通流的稳定。鉴于数值模拟场景和模型参数设置的局限性,下一步将利用实际车辆队列数据对MHOVA模型进行参数辨识与修正,以深入改进和提升MHOVA模型对实际交通现象的模拟能力。
参考文献 (References)
[1]JIN S, HUANG Z, TAO P, et al. Car-following theory of steady-state traffic flow using time-to-collision [J]. Journal of Zhejiang University-SCIENCE A, 2011, 12(8): 645-654.
[2]魏福禄,刘杨.经典跟驰模型的发展综述[J].吉林建筑大学学报,2018,35(4):19-23.(WEI F L, LIU Y. Review of the development of classic car-following models [J]. Journal of Jilin Jianzhu University, 2018, 35(4): 19-23.)
[3]袁娜,史昕,赵祥模.基于改进人工鱼群算法的车辆轨迹规划方法[J].计算机应用,2018,38(10):3030-3035,3047.(YUAN N, SHI X, ZHAO X M. Vehicle trajectory planning method based on improved artificial fish swarm algorithm [J]. Journal of Computer Applications, 2018, 38(10): 3030-3035, 3047.)
[4]李力,姜锐,贾斌,等.现代交通流理论与应用:高速公路交通流[M].北京:清华大学出版社,2011:84-96.(LI L, JIANG R, JIA B, et al. Modern Traffic Flow Theory and Application: Highway Traffic Flow [M]. Beijing: Tsinghua University Press, 2011: 84-96.)
[5]CHANDLER R E, HERMAN R, MONTROLL E W. Traffic dynamics: studies in car following [J]. Operations Research, 1958, 6(2): 165-184.
[6]NEWELL G F. Memoirs on highway traffic flow theory in the 1950s [J]. Operations Research, 2002, 50(1): 173-178.
[7]BANDO M, HASEBE K, NAKAYAMA A, et al. Dynamical model of traffic congestion and numerical simulation [J]. Physical Review E, Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 1995, 51(2): 1035-1042.
[8]HELBING D, TILCH B. Generalized force model of traffic dynamics [J]. Physical Review E, Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 1998, 58(1): 133-138.
[9]JINAG R, WU Q, ZHU Z. Full velocity difference model for a car-following theory [J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Pphysics, 2001, 64(1 Pt 2): Article No. 017101.
[10]PENG G, LU W, HE H, et al. Nonlinear analysis of a new car-following model accounting for the optimal velocity changes with memory [J]. Communications in Nonlinear Science and Numerical Simulation, 2016, 40: 197-205.
