基于改进蚁群算法的铁路乘务排班计划编制

王东先　孟学雷　何国强　孙慧萍　王喜栋

摘 要：為了提升铁路乘务排班计划编制的质量和效率，将乘务排班计划编制问题抽象为单基地、考虑中途休息的多旅行商问题（MTSP），建立以排班周期最小、乘务交路间冗余接续时间分布最均衡为优化目标的单一循环乘务排班计划数学模型，并针对该模型提出了一种启发式修正蚁群算法。首先，构建满足时空约束的解空间，分别对乘务交路节点和接续路径设置信息素浓度;然后，确定基于修正的启发式信息，规定蚂蚁按乘务交路顺序依次出发，使蚂蚁遍历所有乘务交路;最后，从不同的乘务排班方案中选择最优的排班计划。以广深城际铁路为例对所提模型及算法进行验证，并与粒子群算法进行对比。实验结果表明：在相同的模型条件下，采用启发式修正蚁群算法编制的乘务排班计划平均月工时降低了8.5%，排班周期降低了9.4%，乘务人员超劳率为0。所提模型和算法能够压缩乘务排班周期，降低乘务成本，均衡工作量，避免乘务人员超劳。

关键词：铁路;乘务排班计划;多旅行商问题;冗余时间;启发式修正蚁群算法

中图分类号： TP301.6（算法理论）;U292.4（列车运行组织及调度工作） 文献标志码：A

Railway crew rostering plan based on improved ant colony optimization algorithm

WANG Dongxian1， MENG Xuelei1*， HE Guoqiang1， SUN Huiping1， WANG Xidong2

（1. School of Traffic and Transportation， Lanzhou Jiaotong Unirersity， Lanzhou Gansu 730070，China;

2. Wuwei South Station， China Railway Lanzhou Group Company， Limited ， Wuwei Gansu 733000， China）

Abstract： In order to improve the quality and efficiency of railway crew rostering plan arrangement， the problem of crew rostering plan arrangement was abstracted as a Multi-Traveling Salesman Problem （MTSP） with single base and considering mid-way rest， a single-circulation crew rostering plan mathematical model aiming at the smallest rostering period and the most balanced distributed redundant connection time between crew routings was established， and a new amended heuristic ant colony optimization algorithm was proposed aiming at the model. Firstly， a solution space satisfying the spatial-temporal constraints was constructed and the pheromone concentration was set for the crew routing nodes and the continued paths respectively. Then， the amended heuristic information was adopted to make the ants start at the crew routing order and go through all the crew routings. Finally， the optimal crew rostering plan was selected from the different crew rostering schemes. The proposed model and algorithm were tested on the data of the intercity railway from Guangzhou to Shenzhen. The comparison results with the plan arranged by particle swarm optimization show that under the same model conditions， the crew rostering plan arranged by amended heuristic ant colony optimization algorithm has the average monthly man-hour reduced by 8.5%， the rostering period decreased by 9.4%， and the crew overwork rate of 0. The designed model and algorithm can compress the crew rostering cycle， reduce the crew cost， balance the workload， and avoid the overwork of crew.

Key words： railway; crew rostering plan; Multi-Traveling Salesman Problem （MTSP）; redundant time; amended heuristic ant colony optimization algorithm

0 引言

乘务排班计划是乘务计划的一部分，是以列车运行图、乘务交路、相关乘务规则、车站设备条件为基本依据编制的乘务人员（司乘）工作计划。其中，列车运行图包含了待完成的乘务任务，乘务交路规定了乘务人员担当运输任务的固定周转区段，乘务规则限定了乘务人员的工作时间，车站设备条件限制了车站是否是乘务基地及具备司乘人员换乘或休息的条件。

为了合理优化乘务计划编制，有效提升编制效率，乘务计划的编制分为两个阶段：乘务交路计划、乘务排班计划。乘务交路计划和乘务排班计划既有联系又有区别，两者相辅相成，两者既遵循一定的共性乘务规则，同时又具有自身的独特特点。通过乘务交路计划得到乘务交路，利用乘务交路编制乘务排班计划。乘务排班计划编制的优劣直接决定了铁路机务部门的运营效率及机务人员的劳动强度。本文针对乘务排班计划编制问题作出进一步讨论。文献[1]将乘务人员排班计划和飞机排班计划综合考虑，建立了动态规划模型，具有更好的鲁棒性，但是该模型对于求解“点多线长”的铁路乘务计划具有一定局限性。文献[2]将改进的遗传算法应用于乘务排班计划的综合优化问题，虽然编制效率显著提高，但该模型和算法得到的排班计划超劳率偏高。文献[3]将乘务排班计划编制划分为两阶段问题，并用分支定界法进行了求解。文献[4]建立整数规划模型，运用拉格朗日松弛和列生成的组合优化算法，对应急条件下扰动时间不确定的乘务排班计划问题进行研究，但该模型没有考虑乘务人员工作量的均衡性。文献[5]重点研究了工作效率对于乘务计划编制的影响，采用蚁群算法进行求解，但未考虑乘务交路的均衡性。文献[6]利用双重策略蚁群算法编制了乘务交路计划，但是对乘务排班计划的编制没有作进一步研究。文献[7]利用SE（Simulated Evolution）方法编制乘务排班计划，但是对乘务交路计划的编制没有深入研究。文献[8]首次在国内将列生成技术应用到了乘务排班计划的编制，并把乘务排班计划问题抽象成了旅行商问题，但是该算法在求解初始可行解时效率较低。文献[9]将乘务排班计划问题抽象为网络流模型，并利用拉格朗日松弛算法进行求解，但是该算法的迭代步长由经验公式自行设定，缺乏论证。文献[10]将高速铁路乘务排班计划的编制转化为特殊的旅行商问题，并采用改进的蚁群算法进行求解，该模型虽然能够有效提高编制效率，但模型中没有考虑乘务排班的月工时是否超劳。文献[11]将乘务计划编制问题拆分为最优回路构造、回路循环优化和排班三个子问题，并设计了遗传算法进行求解，但是编制步骤繁琐，不利于铁路乘务排班计划的快速编制。文献[12]将乘务排班计划编制问题划分为给定周期、单一循环乘务排班计划两类排班形式，并对非极大排班方案的调整作了深入研究，设计了基于贪婪搜索、集合覆盖的两阶段求解算法，但是该模型没有考虑乘务交路计划与乘务排班计划的协同优化。文献[13]根据现场调研统计的结果，建立了基于乘务人员偏好的乘务交路计划，但是对于复杂交路，没有给出具体的评价值标定方法。文献[14]以交路单元作为列车乘务交路编制基本单位的方法，建立了以最小费用为目标的乘务交路编制优化模型，利用基于贪婪思想的启发式算法进行求解，但是求解精度仍存在改进空间。文献[15]利用禁忌搜索算法完成系统功能设计，能够快速编制高速动车组乘务交路方案，但是机车乘务员容易超劳。文献[16]在已知乘务员标准月工时的前提下，建立了以交路和乘务工时为主要约束条件，以乘务班组最少、乘务费用最低为优化目标的模型，并利用遗传算法进行求解;该模型和算法可有效降低铁路部门乘务费用，但乘务人员工作量较大，不利于行车安全。对上述研究成果进行分析可以看出，国内大多数学者的研究重点主要集中于求得乘务周期最小的排班方案，而关于冗余接续时间相对均衡的排班方案的研究较少。冗余接续时间的均衡性不僅关系到乘务值乘计划的稳定性，还与乘务人员作息是否规律有密切的关系。

根据文献[6]已编制的乘务交路计划，本文在此基础上利用乘务交路，继续编制乘务排班计划。文献[6]将乘务交路计划编制问题抽象为单基地、均衡行驶路程的多旅行商问题（Multi-Traveling Salesman Problem， MTSP），通过引入均衡因子，建立了以乘务交路用时少和子乘务交路间任务均衡为目标的数学模型。针对该模型文献[6]提出了一种双重策略蚁群优化算法，该算法设计了双重信息素及双重策略状态的转移概率，结合乘务交路时空约束规则，设置了双重信息素全局更新策略，在每次迭代结束后，只允许全局最优解释放信息素。在最优路径上，蚂蚁才释放信息素，同时信息素挥发，这点非常重要，因为在信息素更新时的时间复杂度从O（n2）降到了O（n）。设置双重策略状态的转移概率，增加了蚂蚁搜索路径的多样性，又使得更新的路径具有随机性，能够有效避免算法过早地陷入局部最优。本文在总结已有研究成果的基础上，结合铁路乘务规则及其特点，将乘务排班计划编制问题抽象为单基地、考虑中途休息的多旅行商问题，建立以排班周期最小、乘务交路间冗余接续时间分布最均衡为优化目标的单一循环乘务排班计划数学模型，并针对该模型提出了一种启发式修正蚁群算法。该算法对解空间作了改进，构建n维向量Crew-scheduling，设计了基于启发式信息修正的转移概率。通过启发式信息修正的转移概率，使算法在降低问题复杂性的同时，增加蚂蚁搜索路径的多样性，减少算法搜索的盲目性，有效引导算法朝全局最优方向进行搜索。启发式信息在算法运行时，能够指引蚂蚁向压缩乘务交路总接续时长的相邻乘务交路转移。文献[6]选用遗传算法作为对比算法，得出改进的双重策略蚁群优化算法较遗传算法能更快地收敛，解的质量也有大幅提升。本文选用粒子群算法作为对比算法，得出改进的启发式修正蚁群算法较粒子群算法具有更快的收敛速度。同时，文献[6]和本文都运用广深线城际铁路数据作为算例，对设计的模型及算法进行检验。

1 乘务排班计划数学模型的建立

1.1 问题描述

蚂蚁k从不同的乘务交路节点出发，以概率Pkij向相邻乘务交路j转移时，若转移后的连续值乘累计时长小于单双休累计值乘时长标准，则直接转移至乘务交路j，同时更新向量Crew-scheduling，并令值乘累计时长为tcj=tci+ttj;若转移后连续值乘累计时长大于单双休累计值乘时间标准，则按照单双休累计值乘时长标准转移至乘务交路j，同时更新向量Crew-scheduling，令值乘累计时长为tcj=tcj，并将转移后的乘务交路j定为当前节点，继续进行解的构建，直至向量Crew-scheduling中所有元素都为1时完成解的构建。

3）信息素的表示、初始化及更新。

信息素τij表示蚂蚁处在节点i时，接续节点j的重要程度。其中，路径上的信息素初始浓度设定为：

τij（0）=1|A|2-|A|， i≠j

0，其他  （15）

式中，A表示互异乘务区段节点之间的接续频数。

信息素浓度与各乘务交路节点是否参与了最优解的构建成正相关。在最优蚂蚁每次迭代后，路径上的信息素的更新取值设定如下：

τij（n+1）=ρτij（n）+Δτij（16）

Δτij=1/Zibest， eij∈sibest

0，其他 （17）

其中：ρ为信息素挥发因子，0<ρ<1;n代表迭代次数;Δτij为每次迭代过程中的信息素增量。

4）基于启发式信息修正的转移概率。

当第k只蚂蚁在乘务交路节点i时，接续下一个乘务交路j的概率为：

Pkij=[τij]α·[ηij]β∑l∈Vki[τil]α·[ηil]β， j∈Vki

0，其他 （18）

式中：ηij为预见度，表示从乘务交路节点i转移到乘务交路节点j的预见程度;Vki表示蚂蚁待访问的节点集合，随着迭代次数的增加，Vki中的元素不断减少，直至为空，即表示所有乘务交路节点全部遍历完毕;α表示残留信息素的相对重要程度，其值越大，信息素的浓度在转移中起的作用越大;β为预见值的相对重要程度，其值越大，蚂蚁以越大的概率转移到接续时间较短的下一个乘务交路节点。其中对启发式信息进行修正，如式（19）所示：

ηij=

1ttθij-Ts+ω， tci+ttθij≤Tr

1ttθij0+Ts-ttθij01440·1440-Ts+ω，其他 （19）

其中：ttθij为乘务交路接续时间;Tr为单双休接续时长标准;Ts为乘务交路间实际接续时间对应的接续时间标准;ttθij0为初始计算得出的乘务交路间接续计算时长，仅满足乘务交路的正常接续时长标准，即ttθij0≥Ts，但不一定满足单双休接续时长标准;ω为常数，确保当实际接续时间与乘务接续时长标准相同时，式（19）仍成立。所建模型以排班周期最小为优化目标，即乘务交路接续时间最小。对于当前乘务交路，若继续接续后面的乘务交路，并连续值乘累计时长不超过单双休累计值乘时长标准，则乘务交路接续时长为通过初始计算而得的乘务交路接续时长;若接续后的连续值乘累计时长大于单双休累计工作时长标准，则乘务交路接续时长需要由初始接续时长作相应修改，如式（20）所示。

ttθij=ttθij0，tci+ttθij≤Tr

ttθij0+Ts-ttθij01440·1440，其他 （20）

通过分析乘务交路乘务接续时长特点，设计了基于启发式信息修正的转移概率，使算法在降低问题复杂性的同时，减少了算法搜索的盲目性，有效引导算法朝全局最优方向进行搜索;同时，增加了蚂蚁搜索路径的多样性，又使得更新的路径具有随机性，能够有效避免算法过早地陷入局部最优，而进入停滞状态。启发式信息在算法运行时，能够指引蚂蚁向压缩乘务交路总接续时长的相邻乘务交路转移。在算法迭代过程中，启发式信息的修正考虑了接续乘务交路后乘务人员休息的类型，即正常休息或单双休三种情况，并分别进行计算。在算法执行过程中动态地更新，即算法执行至某一时刻时，并不立即接续下一个乘务交路节点，而是先判断既有乘务交路分别选择所有可接续的乘务交路后对应休息的种类（正常休息或单双休），并根据不同乘务人员休息类型及时更新启发式信息，目的在于使乘务交路接续冗余时间最小，同时增加算法的全局搜索能力，加快算法的收敛。

5）评价函数。

本文以式（1）作为评价函数，评价所有解的质量。

6）终止策略。

蚂蚁经过若干次搜索后，找到的解不再改变时，算法终止。

2.2 算法具体实现流程

本文算法具体实现流程如下：

步骤1 令nc←0，k←1，初始化α、β、ρ蚂蚁数量、最大迭代次数等参数，并令乘务排班起始乘务交路节点e←1。

步骤2 将m只蚂蚁放置在乘务交路节点e，构建一个n维向量Crew-scheduling，该向量中的元素代表了所有的乘务交路，所有元素都为0-1变量。当某一元素对应的乘务交路未被选择时，该元素为0;否则为1。初始化向量Crew-scheduling，令所有元素初态为0，并计算乘务交路正常接续时长和累计值乘时长。

步骤3 对于蚂蚁k，计算接续n维向量Crew-scheduling中乘務交路i后的累计值乘时长tci，若tci>TCj，则按式（20）将既有乘务交路与乘务交路j的接续时长转化为单双休接续时长;否则，保持ttθij不变。

步骤4 针对蚂蚁k，根据步骤2中更新后的接续时长计算启发式信息，并得到选择下一个乘务交路j的概率，同时更新n维向量Crew-scheduling，若此时n维向量Crew-scheduling元素全部为1，则转下一步;否则转步骤3。

步骤5 将得到的乘务排班方案中末尾乘务交路节点与起始乘务交路e相连接，完成乘务交路回路的构建。并令k←k+1，若k>m，则转下一步;否则转步骤3。

步骤6 所有蚂蚁构建乘务交路回路，以式（1）作为评价函数，评价所有解的质量，并确定最优解，根据迭代最优解动态更新启发式信息。

步骤7 令nc←nc+1，如果nc小于步骤1中指定的最大迭代次数，则更新n维向量Crew-scheduling，转至步骤2;否则表示所有蚂蚁己完成以乘务交路节点e作为起始节点的乘务排班计划编制。

步骤8 令e←e+1，若e>n，则表示以所有乘务交路为起始节点完成乘务排班计划编制，转下一步;否则转步骤2。

步骤9 算法结束，根据输出的不同乘务排班方案，输出最优解。

3 实例验证及分析

3.1 实验数据

以广深线城际列车为例对本文模型和算法的有效性进行验证。广深线正线全长147km，共设车站7座，列车最高运行速度200km/h，线路起于广州市越秀区广州站，经由广州市广州东站、东莞市东莞站、常平站、樟木头站、深圳市平湖站，终于深圳市罗湖区深圳站。动车组检修基地设置在广州东站接轨的石牌动车检修所。乘务基地设置在广州东站，深圳站设乘务人员公寓，供在深圳驻班或调休的乘务班组休息。

广深线乘务运用情况说明：机务乘务组应遵循早出乘早下班，晚出乘晚下班的原则;所有乘务组在乘务基地进行出退乘作业，广州东—广州乘务值乘方式为双班单司机，广州东—深圳乘务值乘方式为单班单司机。广深线6：00—24：00的城际列车开行方案中，有18对列车为广州至深圳直达列车，57对列车为广州东至深圳直达列车，以广州东站为乘务基地，以深圳站为换乘站，根据文献[6]编制的乘务交路计划可知广深线城际列车按照18条乘务交路运行，如表2所示。

3.2 算例结果

根据1.2节所述乘务规则约束，输入乘务交路时间相关的参数，实验参数可根据现场具体车站的乘务规则作出相应调整。根据广深线调研数据可得，乘务排班相关时间参数设置为：乘务排班计划的正常休息时长标准为不低于960min，但是也不宜过长，否则会影响乘务组织效率，因而将最大正常休息时长设定为1110min。双休最小累计时长标准为2300min，双休最大累计时长标准为2418min。正整数M的取值为2880，ε取值为1 （在正常情况下，根据乘务基地广州东的历史乘务数据，查定得到的数值）。运用本文设计的改进蚁群算法进行求解，其中：信息素重要程度因子α=1，启发式信息素重要程度因子为5，信息素挥发因子取0.2，蚂蚁个数取20，设迭代次数为200，算法重复执行次数为100。在Intel core i7-8550U CPU 1.8GHz、内存8GB的计算机上，运用Matlab R2015b进行求解。

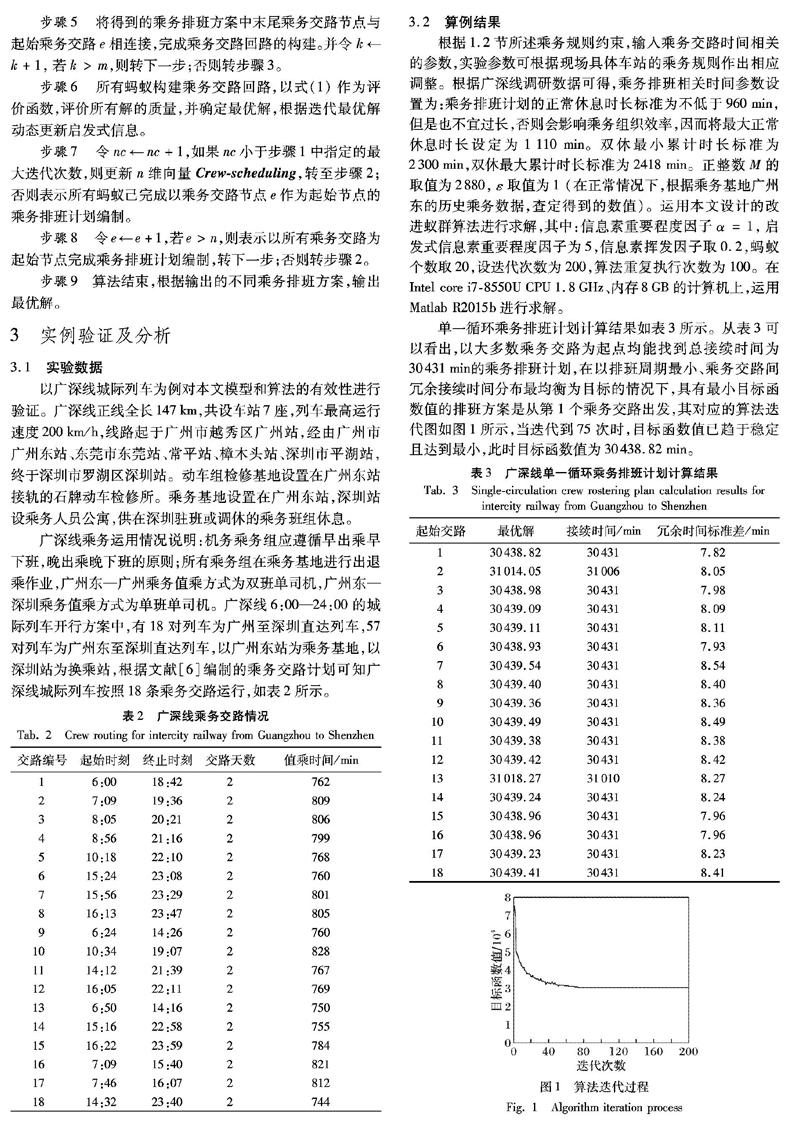
单一循环乘务排班计划计算结果如表3所示。从表3可以看出，以大多数乘务交路为起点均能找到总接续时间为30431min的乘务排班计划，在以排班周期最小、乘务交路间冗余接续时间分布最均衡为目标的情况下，具有最小目标函数值的排班方案是从第1个乘务交路出发，其对应的算法迭代图如图1所示，当迭代到75次时，目标函数值已趋于稳定且达到最小，此时目标函数值为30438.82min。

各乘务交路间冗余时间的均衡性如图2所示。从图2可以看出，乘务交路间冗余接续时间的均衡性比较好。根据计算结果，乘务交路间总接续时间为30431min，乘务人员值乘时间为14100min，所以乘务排班计划总时间为44531min。

3.3 结果评价分析

计算结果的指标如表4所示，分析后可得出如下结论：

1）本文所求乘务排班周期为48d，排班周期和乘务基地所拥有的乘务组数相同。根据计算结果，所有乘务组均连续作业6d后，休息2d。乘务人员在6d值乘时间里，正常累计值乘时间分布在2301～2418min，平均每天值乘6.392～6.717h，符合乘务人员劳动时间标准。整个乘务排班周期内，乘务员的乘务工作安排如表5所示。

指标名称实验结果评价原则评价结果平均月工时178.8h月度最大工时为180h符合最大连续值乘

列数4列连续值乘不得超过

4趟列车符合最大值乘列数5列最大值乘列数不得

超过6趟列车符合最大连续值乘

时间373.8min最大连续值乘时间

不超过480min符合最大值乘时间507min最大值乘时间不超过

540min符合

2）根据优化结果，平均月工时为178.8h，各乘务组的月度工作时间接近规定时间，有效地避免了乘务组超劳的情况，使乘务人员有更充沛的精力值乘后续列车，有效地保障了列车运行安全。调休乘务组和值乘乘务组比例为1/3，比例适中，便于处理临时性应急乘务任务，并保证了乘务任务分配的均衡性。

3）乘务交路间的冗余时间分布在99～124min，提高了乘务排班计划的鲁棒性，使乘务交路的实际接续时间在列车发生突发事件后仍满足接续时间标准。

3.4 算法对比分析

多数学者均采用粒子群算法求解乘务排班计划问题，因此本文以粒子群算法作为对比算法。在同一台计算机上运用Matlab R2015b对本文模型进行求解，均衡因子与上述取值相同，迭代次数为200，算法重复执行次数为100。從多次执行情况来看，其平均收敛代数约在85～95，每次搜索耗时1.8620s，算法总的执行时间为1023.3240s。起始交路为12号乘务交路，较优乘务排班计划的运行结果为31439.4117min。两种算法对比结果如表6所示。通过对比分析可得，与粒子群算法相比，本文设计的改进蚁群算法具有更快的收敛速度，能够使平均月工时降低8.5%，排班周期降低9.4%，乘务人员超劳率为0，从而大幅提升了解的质量。

4 结语

本文建立了以排班周期最小、乘务交路间冗余接续时间分布最均衡为目标的MTSP模型，通过引入冗余时间均衡性，使得模型更具实际意义;同时提出了一种启发式修正蚁群算法，其特点在于采用运行时信息作为启发式信息来指导蚁群的搜索过程，在一定程度上既增加了算法的全局搜索能力，又可以加快算法的收敛，同时避免了传统蚁群算法易陷入局部最优的缺点。

与粒子群算法相比，本文提出的改进蚁群算法效率更高、求解質量更好，对本文模型的求解具有很强的适应性。

本文模型及算法可为铁路机务部门编制乘务排班计划提供有价值的决策支持，对增强铁路机务系统统筹协调能力具有实际意义和帮助，可作为铁路系统乘务管理决策理论的组成部分。本文模型未考虑乘务排班计划与机车周转图的一体化协同编制，对于这一问题的研究将是后续工作的重点。

参考文献 （References）

[1]MERCIER A， SOUMIS F. An integrated aircraft routing， crew scheduling and flight retiming model [J]. Computers and Operations Research， 2007， 34（8）： 2251-2265.

[2]SOUAI N， TEGHEM J. Genetic algorithm based approach for the integrated airline crew-pairing and rostering problem [J]. European Journal of Operational Research， 2009， 199（3）： 674-683.

[3]NISHI T， SUGIYAMA T， INUIGUCHI M. Two-level decomposition algorithm for crew rostering problems with fair working condition [J]. European Journal of Operational Research， 2014， 237（2）： 465-473.

[4]VEELENTURF L P， POTTHOFF D， HUISMAN D， et al. A quasi-robust optimization approach for resource rescheduling [J]. Transportation Science， 2016， 50（1）： 204-215.

[5]陈海平.高速铁路乘务组织理论与优化研究[D].北京：北京交通大学，2013：42-61.（CHEN H P. Research on theory and optimization of crew organization of high-speed railway [D]. Beijing： Beijing Jiaotong University， 2013： 42-61.）

[6]王东先，孟学雷，乔俊，等.基于改进蚁群算法的铁路乘务交路计划的编制[J].计算机应用，2019，39（9）：2749-2756.（WANG D X， MENG X L， QIAO J， et al. Research on railway crew routing plan based on improved ant colony algorithm [J]. Journal of Computer Applications， 2019， 39（9）： 2749-2756.）

[7]阎永光，黄斌.广深线城际列车乘务组排班计划编制方法探讨[J].交通运输工程与信息学报，2010，8（1）：25-29.（YAN Y G， HUANG B. Research on the crew schedule programming method of Guangzhou- Shenzhen intercity trains [J]. Journal of Transportation Engineering and Information， 2010， 8（1）： 25-29.）

[8]程岩岩.我国铁路乘务调度计划编制方法的研究与设计[D].北京：北京交通大学，2007：21-30.（CHENG Y Y. Research and design of domestic railway crew scheduling method [D]. Beijing： Beijing Jiaotong University， 2007： 21-30.）

[9]张哲铭，王莹，陈旭，等.高速铁路单一循环乘务值乘计划优化研究[J].铁道运输与经济，2018，40（1）：21-27.（ZHANG Z M， WANG Y， CHEN X， et al. Research on single-circulation crew rostering plan optimization for high-speed railway [J]. Railway Transport and Economy， 2018， 40（1）： 21-27.）

[10]褚飞跃，田志强，倪少权.高速铁路单循环乘务排班计划编制模型与算法[J].铁道学报，2012，34（7）：1-9.（CHU F Y， TIAN Z Q， NI S Q. Model and algorithm for formulation of the single cycle crew rostering plans of high-speed railways [J]. Journal of the China Railway Society， 2012， 34（7）： 1-9.）

[11]黄珊.机车乘务人员运用问题及其辅助编排系统研究[D].长沙：中南大学，2014：30-44.（HUANG S. Locomotive crew scheduling problem and scheduling assistant system [D]. Changsha： Central South University， 2014： 30-44.）

[12]田志强.高速铁路乘务计划编制优化理论与方法研究[D].成都：西南交通大学，2011：45-72.（TIAN Z Q. Study on theory and methods of crew planning problem of high-speed railway [D]. Chengdu： Southwest Jiaotong University， 2011： 45-72.）

[13]陈旭，李海鹰，王莹，等.放射状路网条件下动车组运用优化研究[J].铁道学报，2017，39（11）：23-29.（CHEN X， LI H Y， WANG Y， et al. Research on optimization of EMU scheduling for radial HSR network [J]. Journal of the China Railway Society， 2017， 39（11）： 23-29.）

[14]李雯，贾富强，杨睿.基于交路单元的高速铁路乘务交路编制模型与算法[J].交通运输研究，2018，4（4）：48-53.（LI W， JIA F Q， YANG R. A model and algorithm of high-speed railway crew scheduling based on routing unit [J]. Transport Research， 2018， 4（4）： 48-53.）

[15]符卓，袁雪莹.高速动车组乘务交路辅助编制系统研究[J].铁道运输与经济，2019（8）：18-21.（FU Z， YUAN X Y. A research on high-speed EMU crew schedule auxiliary preparation system [J]. Railway Transport and Economy， 2019（8）： 18-21.）

[16]杨国元，史天运，张秋亮.铁路客运乘务排班计划编制模型及算法[J].交通运输系统工程与信息，2016，16（4）：159-164.（YANG G Y， SHI T Y， ZHANG Q L. Model and algorithm for railway passenger crew rostering plan [J]. Journal of Transportation Systems Engineering and Information Technology， 2016，16（4）： 159-164.）

[17]马良，朱刚，宁爱兵.蚁群优化算法[M].北京：科学出版社，2008：57-73.（MA L， ZHU G， NING A B. Ant Colony Optimization Algorithm [M]. Beijing： Science Press， 2008： 57-73.）

[18]段海滨.蚁群算法原理及其应用[M].北京：科学出版社，2005：212-232.（DUAN H B. Ant Colony Algorithms： Theory and Applications [M]. Beijing： Science Press， 2005： 212-232.）

This work is partially supported by the National Key Research and Development Program of China （2016YFB1200100）， the National Natural Science Foundation of China （71861022， 61563028）.

WANG Dongxian， born in 1992， M. S. candidate. His research interests include operation management and decision optimization of rail transit.

MENG Xuelei， bon in 1979， Ph. D.， professor. His research interests include operation management and decision optimization of rail transit.

HE Guoqiang， born in 1990， M. S. candidate. His research interests include intelligent algorithm， management optimization of warehousing logistics.

SUN Huiping， born in 1993， M. S. candidate. Her research interests include operation management and decision optimization of rail transit.

WANG Xidong， born in 1993， assistant engineer. His research interests include optimization of railway traffic organization， cargo transportation organization.

收稿日期：2019-06-27;修回日期：2019-09-05;錄用日期：2019-09-12。

基金项目：国家重点研发计划项目（2016YFB1200100）;国家自然科学基金资助项目（71861022，61563028）。

作者简介：王东先（1992—），男，甘肃武威人，硕士研究生，主要研究方向：轨道交通运行管理与决策优化; 孟学雷（1979—），男，山东泰安人，教授，博士，主要研究方向：轨道交通运行管理与决策优化; 何国强（1990—），男，甘肃白银人，硕士研究生，主要研究方向∶智能算法、仓储物流管理优化; 孙慧萍（1993—），女，甘肃定西人，硕士研究生，主要研究方向：轨道交通运行管理与决策优化; 王喜栋（1993—），男，甘肃临洮人，助理工程师，学士，主要研究方向：铁路车流组织优化、货物运输组织。

文章编号：1001-9081（2019）12-3678-07DOI：10.11772/j.issn.1001-9081.2019061118