迁移理论在物理教学中的应用
2019-01-06赖义平宋善炎
赖义平 宋善炎
摘 要:普通高中物理新课标要求用形成的物理观念解决实际问题,新问题的解决要用到先前的知识经验——学习迁移,物理教学中如何做好迁移?文章阐述了迁移理论在物理教学中的建构过程,结合教学实际提出物理学习迁移的策略:以学科思想方法整合知识结构,找准联系;抓问题的本质,加强概括迁移;关注情境间的联系,实现解题方法迁移;加强学科间的横向迁移。
关键词:物理教学;迁移理论;方法策略
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2019)10-0011-4
很多学生反映,能听懂老师所讲的内容,遇到问题却无从下手;解决了一个问题,遇到变式还是无能为力。不能在新的问题情境中做到举一反三,迷失在知识和方法的“此山中”,而不识其本质的“庐山真面目”,即缺乏迁移能力。
何为学习迁移?叶圣陶先生说过“凡为教,目的在于达到不需要教”,只是简单地传授知识和方法,学生不能真正学会学习,不能获得解决问题的能力。所谓“不需要教”即学生已经获得了运用现有知识和经验去解决新问题的能力——迁移能力。简言之,学习迁移即新旧学习间的影响。
查阅知网,最早开始迁移与学科结合的研究在1982年“双基”教学时期,到现在共有4255篇文献,从1982年到2001年提出“三维”目标,共382篇文献,年均20篇;从2001年到2015年提出核心素养,共2529篇文献,年均169篇;从2015年到现在,有1345篇文献,年均336篇。从数据来看,学习迁移的关注度呈逐年递增的趋势,当前深度学习已成为世界各国教育改革的方向,迁移理论是其重要理论基础[1]。可见,无论是在“双基”“三维”还是现在“核心素养”“深度学习”的背景下,学习迁移一直是人们追求的教学目标。
1 正确认识迁移理论
形式训练说由17世纪古希腊罗马提出,认为训练可以促进官能的发展,但詹姆士证明记忆取决于方法而非训练,官能由训练都能得到发展的假说是主观臆想的,没有科学证据。1901年,美国心理学家桑代克提出相同要素说,强调两情境间的相同要素,新课进行旧知回顾,即找新旧知识的联系,但迁移仅由联结决定的观点,把迁移简单机械化了。1908年,贾德提出概括化理论,强调两活动间的共同原理,如课后拓展,概括出原理、方法,促进实际运用;现代迁移关注元认知与迁移,元认知扮演着监控和调节者的角色,从而对自己的学习状况有清醒的认识。
以上几个主要迁移理论有其可取之处,同时也存在各自的局限性。形式训练说指出合理的训练能够增强某方面的技能,但要避免只训练不讲方法。相同元素说为教学提供了指导性思想,学习间的关联是迁移的前提,但不能只讲关联,而忽视了学习者的内在训练过程。概括化理论不能只关注相同原理而不重视情境间的差异,原理要与新情境有机调整结合。因此,要辩证地看待迁移理论,合理、融合地使用迁移理论。
2 迁移理论在物理教学中的建构过程
相对于“双基”目标,“三维”目标下的迁移关注到了学生的情感、态度,在“核心素养”目标下,强调的是积极心态、兴趣、习惯和学习方法。可见,迁移与学科的结合随不同时期教育目标而变,从关注迁移理论本身逐渐向关注学习者心理、情绪、元认知转变。在有关迁移的不同学说中,相同元素说主张建构完整的知识结构,形成能力结构,以观念或核心结构统领各知识的结构关系,找新情境与原结构的关联,建构新概念。概括化理论将问题解决的思想方法概括下来,建构实际问题的模型。形式训练说杜绝机械练习,强调思维和变式训练,多角度发散练习,活学活用。元认知引导学生自我总结、反思及与他人分享学习经验和方法[2]。迁移理论与物理学科结合,要根据物理学科的特点创造性地融合,提出具有物理学科特色的策略方法。
物理問题研究遵循物理学科思想方法。物理学科思想方法是研究物理问题的本质属性、规律和相互关系的方法策略[3],教师要深入研究教材,合理规划课程,找准知识结构和学科思想方法的联系。不仅要找知识间的联系,还要将理论与生活实践结合起来,创造有意义学习经历[4],实现教学是为了培养学生未来职业和社会生活所需的必备品格和关键能力。
物理知识来源于实际生活,蕴含在不同的情境中,忽略研究问题的次要因素,把握主要影响,建立理想的物理模型,包括对象或运动模型。另外,高中物理所研究的问题涵盖力、热、电、光、原,不可能面面俱到。同类问题可能存在本质、原理、思想方法或学科观念的联系,要概括其本质和解决方法。从整体上、更高层次上把握物理知识,才能看到之间的关联,触类旁通,为之后的学习或问题解决提供“活水之源”。遇到新问题,知道大概的研究思路和解决方法,这才是培养解决问题的能力。当前研究认识到了方法的重要性,但拘泥于方法本身,要挣脱方法的桎梏,关注情境间的各种关系,以便调用合理的方法。
物理知识与特定的情境联系在一起,例如,说到牛顿第二定律,有的同学往往会与垫高的斜面联系在一起,而在可直接测绳子拉力的情况下,依然认为要垫高斜面,说明对原情境的本质没理解透。为了避免出现思维定式,就要对概念从多角度去考察,发散的变式训练,在不同的情境中把握概念,达到“去情境化”,使迁移不受特定情境的限制。物理离不开数学推导,而在实际问题中,数理的联系往往不明显,这就需要数理思维,如构建数学模型、转化法等。为了使已获得的方法在新情境中调用有序,需要元认知对其进行管理、反思。
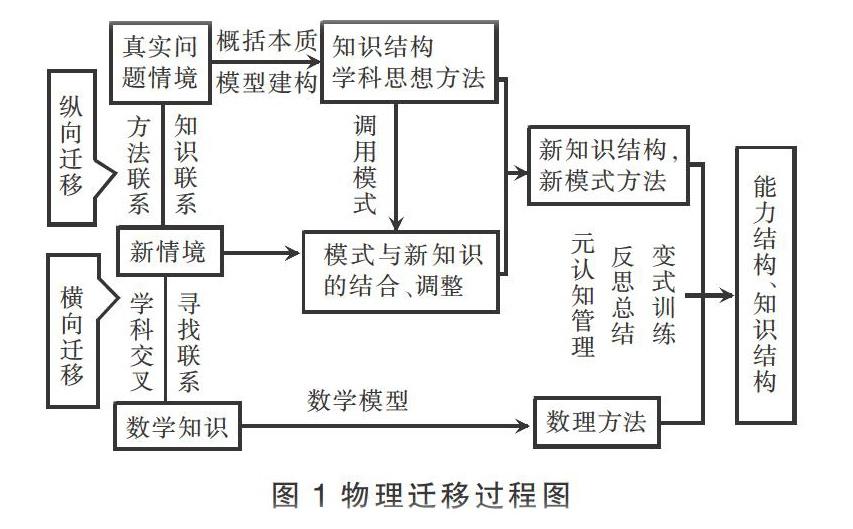
综上,物理学习迁移过程可用图1表示,纵向迁移,基于原有的知识结构、思想方法,找新旧情境的关联,调用原有的模式,进行调整运用,解决问题形成新的知识结构方法。横向迁移,这里讲数理迁移,寻找数理交叉点,用数理思维看问题。所有的方法在元认知的管理、反思、总结下,不断地变式训练,上升为知识结构和能力结构。
3 迁移理论在物理教学中的具体实施
3.1 探寻学科内的纵向迁移
3.1.1 以学科思想方法整合知识结构,找准联系
高中物理新课标强调要“引领学生理解物理学的本质,形成科学思维习惯,增强探究能力和解决问题的能力”。在宏观上构建一个完整的知识和方法体系——物理学科思想方法,相当于在学习过程中有了指导思想,让学习与迁移变得有章法。高中物理知识的编排在难易程度上是递进的。必修部分感性材料多一些,选修部分偏抽象理解,但知识和思想方法是相通的。主要有理想模型法、等效思想、数理方法、归纳与演绎法等。在物理学习过程中,可用学科思想方法作为迁移的主线。
例如,学习电势能这个抽象概念,联想学过的动能、势能,在做功可以引起能量变化的思想方法下,寻找电场力与重力做功的关联,类比得出电势能的一系列规律。再如推导库仑力,已得出F∝1/r2,F∝q1q2,如何得出F的表达式,联想万有引力的推导,先后得出F与距离和质量的关系,推出最终表达式利用的是比例系数法。另外,图像法中,由v-t图像的面积即位移,为变力做功的求法提供了迁移基础,即从F-x图像这个思路找到解决办法。
因此在开始学习一个知识,要概括、总结出其研究方法,在新的问题中,以学科思想方法为指引,寻找新旧知识的联系,让学习迁移有法可依。
3.1.2 抓问题的本质,加强概括迁移
据相关学者对高考题的研究发现,注重基础,模型建构,渗透物理思想方法是高考改革的主旋律[5]。高考考查的知识点不过分强调难,却很灵活,更注重处理物理问题的方法,对知识的灵活运用,或在原有的方法上创新。对物理问题,关键搞清来龙去脉,本质是什么,再适当地拓展,这样有利于学生分析新的物理情境,提升迁移水平。
概括本质:如电表改装,要知道改装电流表、电压表和欧姆表的不同之处,为什么出现刻度均匀与不均匀,很多学生没有深入思考过。从改装表的示数如何表示入手,写出新表与电流计示数的关系式,就一目了然。只有搞清楚以电流计为核心的经典欧姆表的原理,概括、总结出经典欧姆表的处理方法,才能在此基础上拓展、延伸,促進学生对于以电压表为核心的创新欧姆表的原理分析与探索。
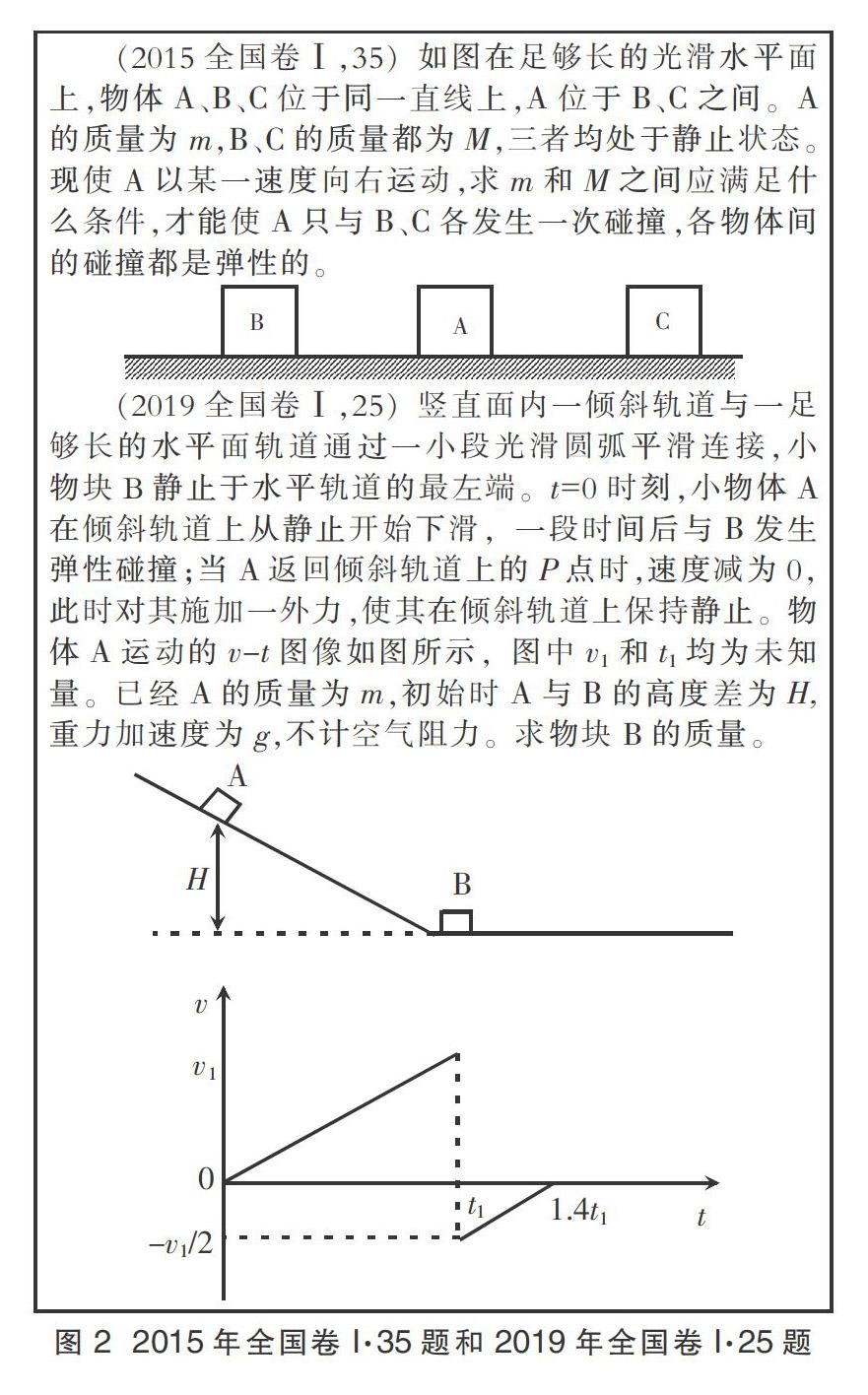
总结模型:2015年、2019年高考的碰撞问题,考查的都是常见的弹性碰撞模型,即物体1有初速度,物体2静止。首次遇到该问题,要概括出该模型发生弹性碰撞后速度的特点及质量改变所产生的现象(图2)。总结经典模型,在遇到类似的问题,抓住核心原理,剩下的工作就是根据新情境进行调整。
我们不主张“题海战术”、盲目训练,没有对问题的分类、方法的指导,就如同无头苍蝇乱撞,解决问题的能力很难提高,而合理安排训练,在每个专题下,对问题进行分类,并进行拓展训练,达到对知识本质的认识和把握。
3.1.3 关注情境间的联系,实现解题方法迁移
人们遇到新问题会努力在记忆中搜索一种有利于当前问题解决的模式[6]。“百度百科”对模式的解释是解决一类问题的方法论。物理问题的解决方法有很多:微元法、图像法、类比法、假设法、极限法、模型法、估算法等。“知网”上关于物理解题技巧的研究有很多,学者们细致地研究了这些方法的内涵和具体步骤,但很少关心学生如何联想到这些方法,我们更应该关注适合此方法的问题情境特征,跳出方法本身,找情境间的关键联系,才能联想到适合新情境的模式方法。在初次接触典型问题,学生自己找到方法,概括方法的使用特点,遇到适合该方法的新情境,挖掘与之前情境的深层关系,实现方法迁移。
例如微元法,匀变速直线运动位移与时间的关系和弹簧的弹性势能两情境间存在着这样的关系:变速、变力(变化),位移、形变量细分可看成匀速、恒力(微分、近似),若足够细分,累加起来可解决问题(极限、累加)。找到了问题情境间的深层关系——微分法,在遇到导体棒在匀强磁场中做减速运动通过导体的电荷量问题,发现也具有上述的关系,而电流与小段时间的乘积累加就是电荷量,从而确定采用微元法。
教师要指导学生经常梳理方法,对方法进行分类,不断地进行反思,实现对自己的学习方法、策略进行自我管理和监控,在知识结构上端形成方法结构,从而更好地实现方法迁移。
3.2 加强学科间的横向迁移
我们常说“数理不分家”,在这两门自然学科发展的历史长河中,数学的发展促进了物理学的发展,物理离不开数学计算,而物理学的发展也为数学作出了重要贡献。例如,牛顿和莱布尼茨作为微积分学的奠基人,他们的贡献早已载入数学史册。在物理问题解决过程,运用数学方法能够方便问题的解决。
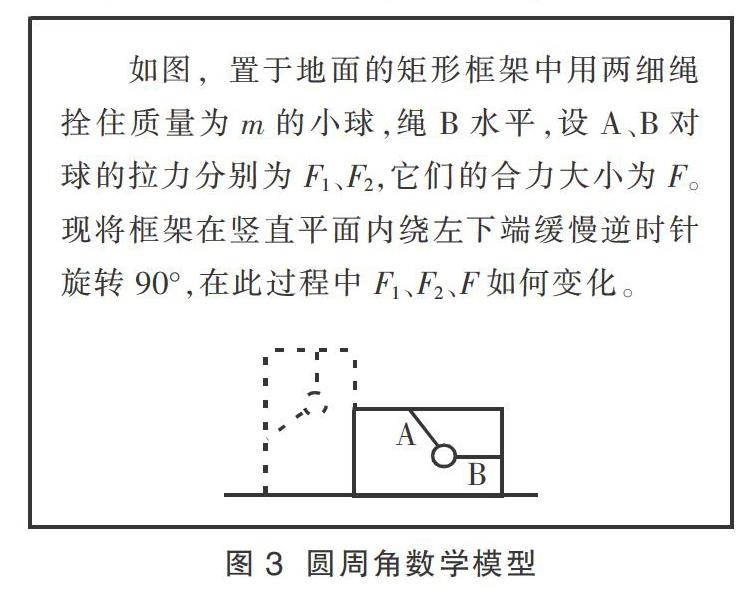
构造数学模型:有些物理问题,满足某个数学模型,要善于分析其中的条件,将物理问题构造成数学模型。如图3动态平衡问题,判断各力的变化。通过受力分析,将不变的合力构造成圆周角的定弦,将不变角的补角构造成圆周角,闭合的力的矢量三角形内嵌于圆中,即构造数学圆周角的模型处理此动态平衡问题。
转化法:先进行常规物理角度的分析、思考,发现与数学间的交叉点,建立起与数学间的关系,从而将物理问题转化为数学问题。例如,两杆间绳挂衣架问题,通过对重力、绳拉力、角度的常规受力分析,发现角度可转化为两杆间距与绳长的关系,即将力的动态问题转化为求角度问题。
习题教学中,我们也可从数学方法的角度对物理问题进行分类,养成从数理结合的层面分析问题,形成数理思维。
4 结 语
完整的知识和方法结构是建立新旧知识联系的前提。对新问题情境要提取关键信息,找到与旧情境的深层关系,以便找准方法,将方法与新信息建立联系的过程,就是培养学生的创新能力、科学思维能力的过程。从数理角度分析物理问题,训练数理思维。适当进行变式训练,达到对知识的认识不受特定情境制约,即抓住了本质。经常对已有的知识、方法结构进行总结、反思,上升为自身的一种问题解决和迁移能力。只有正确认识迁移理论,扎根物理学科,才能提出有物理特色的迁移策略,而物理的迁移研究又完善和充实迁移理论。
参考文献:
[1]孙妍妍,祝智庭.以深度学习培养21世纪技能——美国《为了生活和工作的学习:在21世纪发展可迁移的知识与技能》的启示[J].现代远程教育研究,2018(3):9-18.
[2]马亚鹏,杨威虎.物理教学中学生知识迁移能力的培养[J].物理通报,2014(5):120-122.
[3]司德平.高中物理必修1学科思想方法教育内容分析[J].物理之友,2016,32(11):1-5.
[4]宋善炎,丁向阳.“有意义学习”与“有意义的学习经历”[J].教育科学研究,2010(3):63-65,69.
[5]李雪,史策,梁林艳,等.基于核心素养的高考物理试题分析与思考[J].教学与管理,2019(12):82-84.
[6]National Research Council(2012a). Education for Life and Work: Developing Transferable Knowledge and Skills in the 21st Century[M].Washington, DC: National Academies Press.
(栏目编辑 赵保钢)
