RT位移模式挡土墙非极限被动土压力探讨

李永刚 周慧珍

（1.太原理工大学水利科学与工程学院 山西太原 030024；2.太原理工大学图书馆 山西太原 030024）

挡土墙广泛应用于水利、土木和交通等行业当中，其上的土压力是挡土墙设计的重要依据。目前，挡土墙土压力的计算理论仍不完善，一是挡土墙绝大多数情况下回填土体处于非极限状态[1]，二是由于地基不均匀沉陷和水压力的作用等，使挡土墙可能发生平移（T）、绕墙顶转动（RT）、绕墙底转动（RB）或组合移动[2]，这使得挡土墙土压力计算没能形成系统理论。对不同墙体位移模式的非极限状态土压力进行研究，具有一定的实际价值和理论意义。本文拟对绕墙顶转动（RT）位移模式的挡土墙非极限状态被动土压力计算进行探讨。

1 挡土墙非极限状态土压力计算参数

1.1 内、外摩擦角

墙后土体从静止状态到极限状态是一个渐变的过程，墙和土之的间外摩擦角δ与填土的内摩擦角φ随着挡土墙位移的增大逐渐发挥出来，直至达到最大值。在非极限状态下，δ处于初始状态外摩擦角δ0与极限状态外摩擦角δm之间，φ也处于初始状态内摩擦角φ0与极限内摩擦角φm之间。δ和φ都是挡土墙位移量S的函数[3]：

式中：Kd为考虑墙体位移对δ和φ的影响系数，S为挡土墙平动位移量（注：RT位移模式挡土墙背面各点位移不同，各计算点的δ、φ不同），Sc为内、外摩擦角达到最大值时所需的墙体平动位移量。显然，静止状态时 S=0，φ=φ0、δ=δ0；极限状态 S=Sc时，φ=φm，δ=δm，δ和 φ 的值随墙体平动位移 S 的增大而增大。

φ0可由改进的库仑方程式求解[4]：

式中：k0为静止侧压力系数，对于正常固结土，k0=1-sinφ，近似取 δ0=φ0/2。

参考文献［5］，微元的层间摩擦角 φ′=0.5φ。

1.2 准滑移面倾角和被动土压力系数

挡土墙挤压土体而未达到极限位移时，填土的内摩擦角只有部分发挥，填土的准滑移面倾角近似按库仑理论计算：

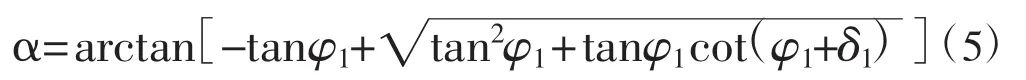
式中：φ1为墙后不同高度土体发挥出来之内摩擦角平均值；δ1为墙后不同高度墙和土接触面上发挥出来的外摩擦角之平均值。

参考文献［6］，取实用的被动土压力系数为

对于粗糙墙背，θ=45°+φ/2，KP为朗肯被动土压力系数：

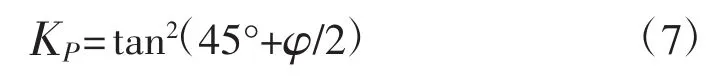
2 RT位移模式挡土墙被动土压力计算

2.1 计算模型及土压力分析

采用库仑土压力计算理论假定，假设RT位移模式挡土墙后土体产生准滑移面，并在滑动土楔当中取水平薄层微分单元，如图1，微元上各个面上作用有正应力和剪应力，它们就是墙背、不动土体对微元的作用——单元两侧的正压应力、剪应力，以及其相邻微元之间的作用——上、下面的正压应力、剪应力。

根据作用于单元体上的竖向力平衡条件得：

式中：b1=（H-y）/tanα

b2=（H-y-dy）/tanα

dw=γ（H-y）dy/tanα

忽略不计二阶微分量，整理（8）式得：

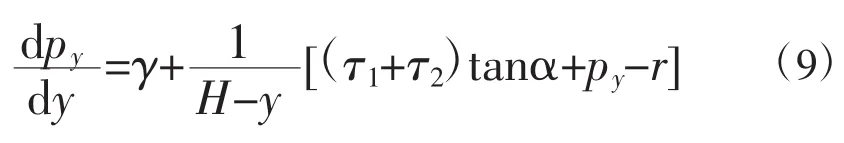
图1 计算简图

考虑无黏性土，令：

由水平微元的水平方向力平衡条件得：

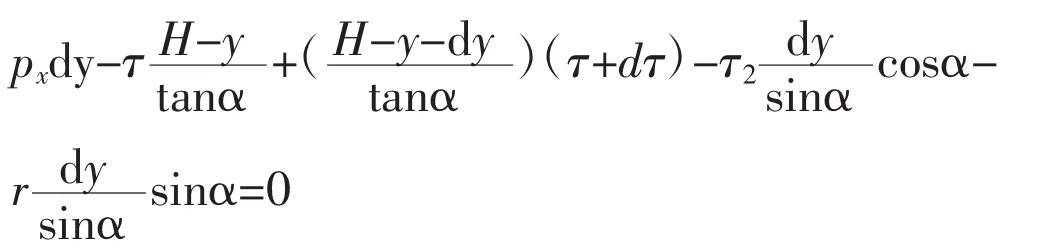
不计二阶微分量，简化得：

无黏性土层间剪应力：

式（9）、（11）联解，整理得：

式（13）为RT位移模式非极限状态下水平微元的基本方程，由其解得垂直土压力，再乘以被的土压力系数，即为被动水平土压力。

2.2 基本方程求解和土压力的计算

式（13）为一阶微分方程，对于RT位移模式非极限状态，墙体转动一定值的情况下，墙后高度不同的各个计算点水平位移不同，其内、外摩擦角的大小各不相同，相应的被动侧压力系数K随y而变，式（13）中的参数A、D也随y变化。当y在某一较小范围内变化时，K、A、D的变化不大，可假定三者为常量，由此得式（13）通解：

由y=y0时py=py0的边界条件，可得积分常数C和挡土墙水平土压力：

式（14）～（16）的求解可利用数值计算方法，从墙顶到墙底划分墙高若干段，各段的K、A、D取常量，进行计算：初始条件为y=0和填土表面均布荷载py0，第一段由此确定（15）式之常数C、该段垂直土压力和水平土压力得之；第1段底部的垂直土压力作为第2段的初始条件，第2段相应的常数C、垂直土压力和水平土压力得到……；第i段底部的土压力作为第i+1段的初始条件，依次得到沿墙高各段的垂直土压力、水平土压力。

3 算例分析

取参考文献［7］中的模型试验参数：挡土墙高度H=1.0 m，砂土容重 γ=15.6 KN/m3，填土内摩擦角 φ=34.2°，墙土外摩擦角 δ=2φ/3=22.8°，土体达到被动极限平衡状态挡土墙所需要的平动位移量Sc/H=8.5%。为比较分析，取RT位移模式墙底的最大位移S1与墙高H之比 S1/H=5.5%（情况1，即 S1/Sc=0.65）和 S1/H=11.6%（情况 2，即 S1/Sc=1.36）进行计算。

令 δ0=φ0/2，静止土压力系数 k0=1-sinφ=1-sin34.2°=0.44，由式（4）进行试算可得 δ0=10°、φ0=20°。经数值计算，得到情况1、情况2的墙体被动水平土压力分布如图2。理论计算结果和试验结果基本一致。在埋深（y）小于0.5H时，墙体位移和土压力系数较小，被动土压力近似线形分布；埋深超过0.5H并逐渐加大时，墙后计算点的水平位移、土体摩擦角发挥值和被动土压力系数也逐渐增大，垂直土压力和水平土压力快速增大，土压力分布曲线呈上凹形。情况1的墙底最大位移小于极限位移，其被动土压力总值27.51 kN，接近朗金土压力27.8kN，而远小于库仑土压力62.82kN，情况1的总土压力作用点距墙底0.22H。情况2的墙底最大位移大于极限位移，其被动土压力总值38.15 kN大于朗金土压力，仍小于库仑土压力，总土压力作用点距墙底0.20H。情况2的墙底最大位移较情况1的相关值成倍增大，被动土压力总值不会成倍增加。

图2 RT位移模式土压力分布

4 结语

借助准滑移面方法研究RT位移模式非极限状态被动土压力，结果表明：绕墙顶转动挡土墙非极限状态被动土压力为凹曲线分布，越靠近墙底，被动土压力增大越快；转动越大，被动土压力越大，其合力作用点越低，合力作用点在墙高的下三分点以下。