汾河流域节水灌溉发展水平评价指标权重的确定

狄 帆

（山西省水利水电科学研究院 山西太原 030002）

0 引言

对汾河流域节水灌溉发展水平的准确评价，是正确认识汾河流域节水灌溉发展水平、推动本区域节水灌溉发展的基础，是制定区域节水政策、方案和措施的科学依据。近年来，节水灌溉发展水平综合评价已经由最初的定性描述分析或定量数据比较发展到定性与定量相结合[1]，由依靠主要指标构建简单的评价体系发展到利用多指标或多目标构建综合评价体系。

在统计综合评价中，权重的大小反映了评价指标在整体评价中的相对重要程度。权重越大则该指标的重要程度越高，对整体的影响就越大。反之权重越小则该指标的重要程度越小，对整体的影响越小。对汾河流域节水灌溉发展水平进行评价时，体系中指标的权重直接影响到节水灌溉发展水平评价的准确性和可靠性，因此选择合适的指标权重计算方法至关重要。

根据计算权重原始数据的来源，指标体系权重的确定方法有主观赋权法、客观赋权法和组合赋权法。主观赋权法是基于决策者的经验或偏好，通过对各指标重要性进行比较而赋权的方法，包括专家评分法、层次分析法、灰色关联分析法等；客观赋权法是根据收集到的信息客观计算出各指标重要程度的方法，有熵权法、主成分分析法、变异系数法等；组合赋权法是将主客观相互融合的综合评价方法，既能体现主观能动性，又有客观分析，实用性较好，已用于各个领域的指标权重计算，苏贤保等人将综合权重法用于西北典型区域水资源脆弱性的评价研究[2]；郭彦英等人将AHP法用于确定地表水水质综合评价指标权重[3]，郝洋等人将AHP－熵权法用于地下水水质模糊综合评价[4]；王琼等人将主成分分析法和熵权法用于河流生境质量的评价[5]；刘大海等人将AHP－熵权法用于海岛海岸带脆弱性评价[6]。

目前，国内外对农业节水灌溉水平评价指标体系权重的计算方法有层次分析法、主成分分析法、人工神经网络法、模糊评价法及灰色关联分析法等方法[7-10]。以上方法虽然有各自的优点，但也有其局限性，如灰色关联分析法，数学处理简单，能使用样本全部信息，避免主观因素的影响，但部分指标最优值难以确定。专家评分法在缺少统计资料时可以做出定量评价，但专家的主观倾向性不容忽视。每种方法的单独使用都不能客观、全面地反映与区域性节水灌溉发展现状。因此，本文将主观赋权法与客观赋权法相结合，采用层次分析法与熵权法确定体系指标的综合权重[11]，以期得到汾河流域节水灌溉水平的科学合理评价。

1 层次分析法简介

层次分析法（AHP，The Analytic Hierarchy Process）是美国著名运筹学家、匹兹堡大学教授T.L.Saaty20世纪70年代提出的一种将定性和定量分析结合的多准则决策分析方法[12]。其基本原理是：将评价对象视为一个系统，根据系统的性质和总目标将研究对象分解成不同的要素，并按照要素之间的隶属关系和相互关联度将其从高到低排成若干层次，从而建立一个多层次的分析系统。它将决策者的主观思维逻辑数字化、严谨化，增强决策依据的准确性，其结果更为客观、科学，在解决难以完全用定量方式分析的复杂问题时尤为适用。

层次分析法是基于问卷调查、电话调查、现有统计资料等形式对体系定性和定量指标进行调查，依据专家意见和建议主观赋权。指标权重是由专家根据知识和经验判断的得出，这样一定程度上比较充分反映专家的知识和经验，但往往会因为主观个人因素和研究人员的知识经验的局限性而造成偏差，具有较强的主观随意性。

2 熵权法简介

熵权法利用系统评价指标的熵值所提供信息量的大小决定指标的权重。通过指标的信息熵计算，得到的熵值越小，说明指标值的变异程度越大，提供的信息量越大，其权重越大。反之，某指标的熵值越大，说明指标值的变异程度越小，提供的信息量越小，其权重越小。

熵权法通过收集客观信息，以事实为基础进行计算，消除了信息之间的重叠性，有很强的说服力。但是未反映研究人员的经验，同时易受离散极值的影响，结果有时与实际情况不符，难以得到公认。

3 指标体系的建立

指标体系的建立充分考虑汾河流域水资源利用情况和高效节水灌溉技术推广应用情况，选择能反映汾河流域节水灌溉发展水平的关键性指标。

汾河流域节水灌溉发展水平综合评价指标体系包括工程措施、节水管理措施、农艺措施三个体系专题指标，以及分属于各个专题指标的单项指标。具体评价指标体系见图1：汾河流域节节水灌溉发展水平综合评价指标体系。其中：定性指标为政策法规、政府支持、宣传教育、公众参与、技术推广体系建立；定量指标为灌溉用水量占总用水量的百分比、节水灌溉面积占有效灌溉面积的百分比、亩均用水量、灌溉水利用系数、计量收费普及率、管灌面积占有效灌溉面积的百分比、微喷灌占有效灌溉面积的百分比、粮食平均亩产量、农村居民人均纯收入。

图1 节水灌溉发展水平评价指标体系

4 指标权重确定

4.1 AHP法指标权重确定

4.1.1 构建判断矩阵

经专家全面分析每个因素的地位和作用，对每一层次中各指标相对于上一层的重要性进行两两比较，采用1～9比例标度法构造出比较判断矩阵。分别对每一层次的评价指标的相对重要性用准确的数字量化表示。判断矩阵中数字1表示两元素对某一属性具有同样重要性；数字9表示两元素相比较，前者比后者极端重要，中间数字表示意义依次类推，最终得到4个判断矩阵。构造的判断矩阵和计算结果见表1～表4。

表1 A－B判断矩阵

表2 B1－C1～C6判断矩阵

表3 B2－C7～C12判断矩阵

表4 B3－C13～C14判断矩阵

4.1.2 判断矩阵求解

对于判断矩阵A，利用方根法对矩阵进行求解，计算步骤如下：判断矩阵每一行元素乘积，构造一个新的向量；新向量的每个分量开n次方；所得向量进行归一化处理，即为判断矩阵的特征向量。

计算公式如下：

以A－B判断矩阵为例，

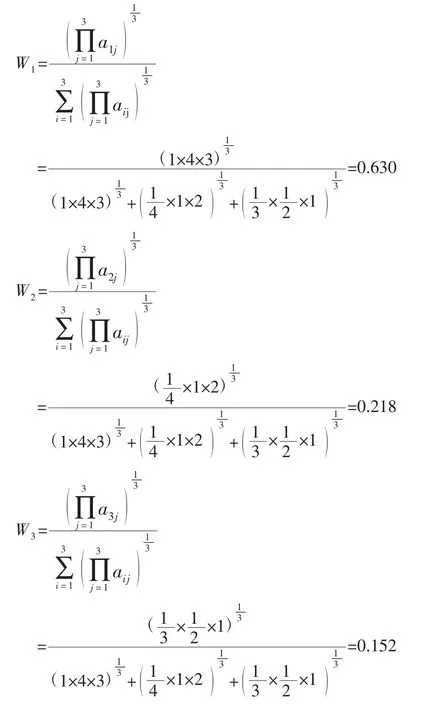
求得特征向量 W=（0.630，0.218，0.152）T，即指标权重。计算最大特征值λmax。

4.1.3 一致性检验

为了检验判断矩阵的一致性，需要计算一致性指标CI。

当维数为3时，相应的平均随机一致性指标RI=0.58，所以一致性比例CR为：

CR＜0.1，表明判断矩阵符合一致性要求。

其余各个指标层的权重值均按此方法计算，结果见表1～4。经一致性检验，各个判断矩阵均具有较好的一致性，因而所得的指标权重是可以接受的。

4.1.4 AHP法综合权重

得到各个层次、各个评价指标的权重值后，根据层次总排序原理，计算各元素对总目标的相对权重，即综合权重。综合排序权重的计算自上而下，将单一准则下获得的权重进行组合，求得各评价指标对总目标的相对权重值。

组合公式为：

式中，Pi是第一层各指标获得的权重值；

Qi是第二层各指标获得的权重值。

AHP法各指标的综合权重如表5所示。

表5 评价指标综合权重

4.2 熵权法指标权重确定

4.2.1 定性指标量化

在汾河流域节水灌溉发展水平综合评价指标体系中包括5个定性指标和9个定量指标，其中定性指标包括政策法规、政府支持、宣传教育、公众参与、技术推广体系建立。定性指标量化方法如下：

采用问卷调查的方式对40个县级行政区域水行政管理部门管理人员进行调查，做出评估，评估结果分为好、较好、一般、较差、差等5个等级，采用指标量化公式对定性指标进行分值量化，“好”等级P1=10分，“较好”等级 P2=8 分，“一般”等级 P3=6 分，“较差”等级P4=4分，“差”等级P5=2分；定性指标量化公式如下：

式中：M代表汾河流域一个地市某项定性指标的量化值；

F代表汾河流域一个地市同等级的样本数；

N代表汾河流域一个地市样本总数；

将定性指标量化结果加入汾河流域的定性指标的综合评价指标体系，形成指标评价系统，具体结果见表6。

4.2.2 数据归一化处理

由于各个评价指标的单位、量纲、数量级不同，会对评价结果造成影响，因此要对数据进行归一化处理。评价方案中除灌溉用水量占总用水量的百分比和亩均用水量为成本型指标，其余均为效益型指标。

对于效益型指标，归一化的公式为：

对于成本型指标，归一化公式为：

式中：yij、Zij分别为归一化处理前后第i个评价对象的第j个指标值；yj为所有评价对象中的第j个指标的原始值。yjmax、yjmin分别为j第个指标在所有评价对象中最大、最小值。

4.2.3 求基于指标的评价对象的比重

式中：n为评价指标个数。

4.2.4 计算第j个评价指标熵值

公式如下：

表6 汾河流域节水灌溉综合评价体系量化指标

式中：Hj为第j个评价指标熵值。

4.2.5 确定指标权重

利用公式（7）计算第j个评价指标的熵权值βj。

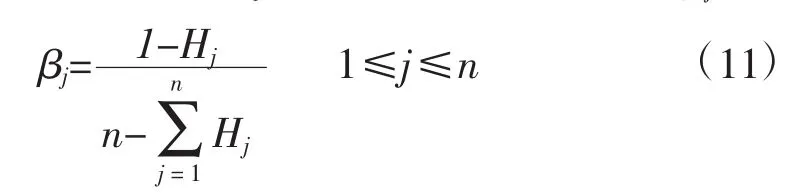
计算结果如下：客观权重向量矩阵β=（0.0798，0.0635，0.0740，0.0626，0.0691，0.0722，0.0683，0.0793，0.0712，0.0766，0.0730，0.0692，0.0713，0.0712）

4.3 综合权重确定

鉴于主客观权重确定方法存在的缺陷与不足，在之前模型研究经验的基础上，将主观赋权法和客观赋权法合理的结合起来，尽量消除两种方法的弊端，得到各个评价指标的综合权重。综合赋权公式如下：

式中：Wj——评价指标j的综合权重

αj——评价指标j层次分析法赋予的权重值；

βj——评价指标j熵权法赋予的权重值；

Wj——评价指标j的综合权重。

得到调整后的指标综合权重表，如表7所示。

表7 AHP和熵值法结合确定的指标权重

4.4 结果分析

5 结语

本文考虑到主客观赋权法存在的缺点与不足，立足于主客观结合赋权方法的现状，采用层次分析法与熵权法相结合的赋权方法，确定了汾河流域节水灌溉水平综合评价体系中各个指标的综合权重，将专家的经验知识和各个数据信息充分结合，既体现了专家的个人意向，实现了专家个人偏好的合理表达，又能反映指标的客观特性，具有较强的实用性和可操作性。可为相关评价体系指标权重的确定提供参考。