Transient peristaltic diffusion of nanofluids: A model of micropumps in medical engineering *
2019-01-05DharmendraTripathiShashiBhushanAnwarNoreenSherAkbar
Dharmendra Tripathi, Shashi Bhushan, O. Anwar Bég, Noreen Sher Akbar
1. Department of Science and Humanities, National Institute of Technology, Uttarakhand – 246174, India
2. Department of Mechanical Engineering, Manipal University, Jaipur, India
3. Department of Aeronautical and Mechanical Engineering, University of Salford, Manchester M54WT, UK
4. DBS & H CEME, National University of Sciences and Technology, Islamabad, Pakistan
Abstract: Peristaltic micro-pumps offer an excellent mechanism for delivery of a variety of medicines including drugs, corneal solutions etc. The surge in deployment of nanoparticles in medicine has provided new potential for such pumps. In light of this we investigate the time-dependent peristaltic flow of nanofluids with diffusive effects through a finite non-uniform channel, this geometry being more representative of real micro-pumps. Creeping flow is taken into account (inertial forces are small compared with viscous forces) i.e., Reynolds number is low (R e < 1) and wavelength is also taken to be very large. The Buongiorno formulation for nanofluids is employed with an Oberbeck-Boussinesq approximation. Closed-form solutions are developed for the non-dimensional governing equations subject to physically realistic boundary conditions. Mathematica symbolic software is employed to evaluate the evolution of nanoparticle fraction, temperature, axial velocity, transverse velocity and pressure difference distribution along the length of the pump channel with variation in thermal Grashof number, basic-density (species i.e., mass) Grashof number, Brownian motion parameter and thermophoresis parameter.
Key words: Unsteady flow, peristaltic pumps, nanofluids, medical engineering, diffusive process, grashof number, thermophoresis
Introduction
Peristaltic micro-pumps have emerged as promising mechanical pumps which exploit the biologically efficient peristalsis mechanism to emulate wave-like contractions/expansions of a tube-shaped organ,resulting in forward motion of fluids. This mechanism is known to mitigate backflow (retro-flux) which is problematic in alternative medical pump systems.Aspects of peristaltic pump technology have been described lucidly by Teymooir and Abbaspour-Sani[1],Wang and Lee[2]. Transient flows in peristaltic pumps are in particular of considerable interest and provide a better understanding of the dynamics and efficiency of such systems[3]. Although most analytical studies of peristaltic flows have been constrained to infinite tubes, several investigations have considered finite length tubes, notably Li and Brasseur[4]. More recently non-Newtonian extensions of the Li-Brasseur study were presented utilizing a power-law fluid model by Misra and Pandey[5]. Further extensions in this direction have been presented for numerous rheological fluids by Tripathi[6], Tripathi and Bég[7], Grosjean et al.[8]who have synthesized a robust peristaltic pump at Caltech. These studies have demonstrated that the finite nature of the transport conduit exerts a substantial influence on peristaltic flow characteristics.
Nano-science and nano-technology have also stimulated great attention in recent years, largely propelled by the continuous miniaturization of existing technology and improvement in performance of medical devices at smaller scales. A subsection of nanomechanics is nanofluid mechanics, pioneered by Choi[9]which addresses the intelligent modification of macro-fluids using carefully designed nano-particles.This has had a diverse impact in medical engineering,to the extent that a Journal of Nanofluids has been launched in the USA[10], and one of many with a large focus on nano-technological fluid mechanics including ASME Journal of Nanotechnology in Engineering Medicine[11]. Important applications of these medical nanofluids which are revolutionizing clinical care include anti-bacterial wound treatment suspensions[12], respiratory tracking mechanisms[13], magnetic biopolymers for drug coating to enable faster tracking to cancerous zones[14], pharmaco-dynamics(drug delivery)[15-17]and protein identifications[18].Fluid dynamics models for nanofluid transport have been developed by a variety of groups worldwide,notably by Buongiorno[19]at MIT. His model emphasizes the thermophoresis and Brownian motion mechanisms for nano-enhanced performance and is robust for adoption in peristaltic flows. Progress has continued in nanofluid dynamic simulation. For example mathematical models for thermal instability in a porous medium saturated by a nanofluid and convection of nanofluids with single and double diffusion have been reported by Nield and Kuznetsov[20-22]. In other developments, a Predictor homotopy analysis for nanofluid flow through flexible permeable walls and unsteady MHD free convective flow from a permeable stretching vertical surface in a nano-fluid has been considered by Freidoonimehr et al.[23-24]. An analytical approach for entropy generation for Casson rheological nanofluids induced by a stretching surface has been presented by Abolbashari et al.[24].
Relatively sparse studies of peristaltic transport of nanofluids have been communicated. Of the mathematical studies conducted the vast majority have addressed infinite straight or curved channels including Akbar and Nadeem[25], Aly and Ebaid[26]for slip flows, Mustafa et al.[27], Akbar et al.[28]. While mathematically rigorous, these studies have neglected a serious interpretation of the nanofluid characteristics on real performance in peristaltic systems. Along with the focus on finite channels, in the present study we examine non-uniform (diverging) channels and also place greater emphasis on the Brownian motion and thermophoretic as well as multiple Grashof number effects in peristaltic transport of nanofluids. Nanofluid transport involves both heat and mass transfer and the interaction of both diffusive phenomena. The model developed examines the interactional influence of diffusive process and nanoparticles on time-dependent peristaltic flow through a finite length non-uniform channel. The coupled differential equations are solved by taking the low Reynolds number and long wavelength approximation. Solutions are benchmarked for the Newtonian case with the previous results of Li and Brasseur[4]. The evolution of nanoparticle fraction profile, temperature profile, velocity profile, and pressure difference across the finite length nonuniform channel is visualized using Mathematica software. This work extends the earlier uniform channel model presented in Ref. [7]. This model is applicable to the simulation of nanofluid peristaltic micro-pumps in biomedical engineering.
1. Geometric model for peristaltic micropump flow
The geometric model for the peristaltic transport of nanofluid via a non-uniform finite channel, as depicted in Fig. 1 is taken as
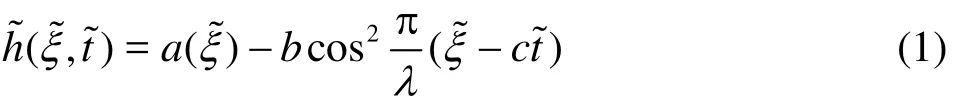

Fig. 1 (Color online) Geometrical model for non-uniform peristaltic micropump flow
2. Mathematical model
The peristaltic micro-pump geometry is approximated by a finite channel with non-uniform sinusoidal waves propagating along the surface. The channel walls are assumed to be distensible and identical in constitution. Damping characteristics are ignored. The nanofluid model employed is adapted from Buongiorno[22]. In the original model, although numerous mechanisms are postulated for convective transport in nanofluids with a two-phase non-homogenous framework including diffusiophoresis, the Magnus effect, fluid drainage, gravity, inertia,Brownian diffusion and thermophoresis, only the last two mechanisms are essentially dominant in the low-Reynolds number regime (laminar flows). Furthermore a dilute nanoparticle suspension is considered here. The magnitudes for temperature ()T and nanoparticle fraction ()F at the center line (=0)η and the wall of the channel (=1)η are denoted by,and,respectively. Under the usual Boussinesq approximation, with an appropriate reference pressure, the transport equations for the regime are respectively[19-22]with the following assumptions:(1) laminar incompressible flow, (2) no chemical reactions, (3) negligible external forces, (4) dilute mixture, (5) negligible viscous dissipation, (6)negligible radiative heat transfer, (7) nanoparticles and base fluid locally in thermal equilibrium.
Continuity equation

Axial momentum equation
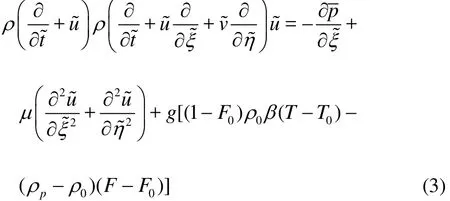
Transverse momentum equation
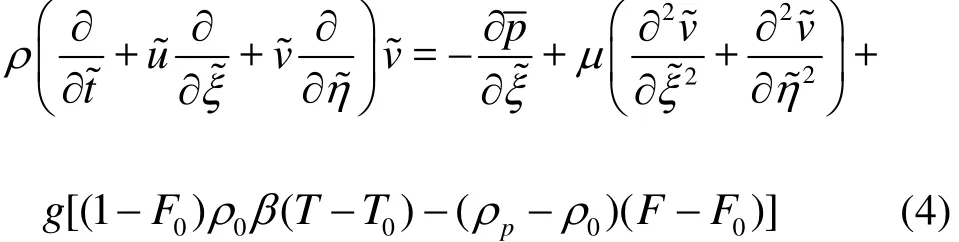
Energy equation
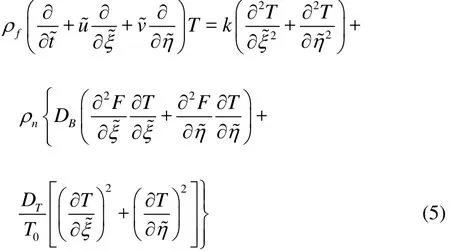
Conservation equation for the nanoparticles, in the absence of chemical reactions

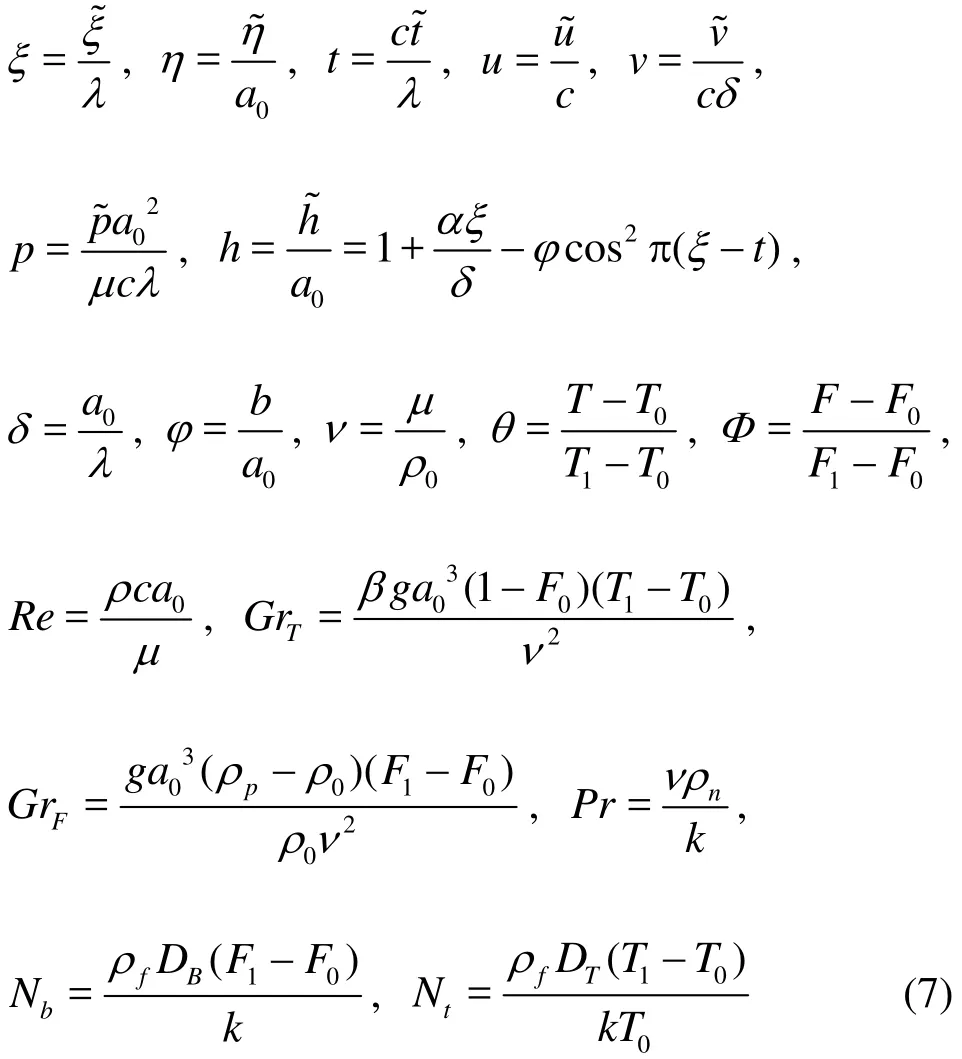
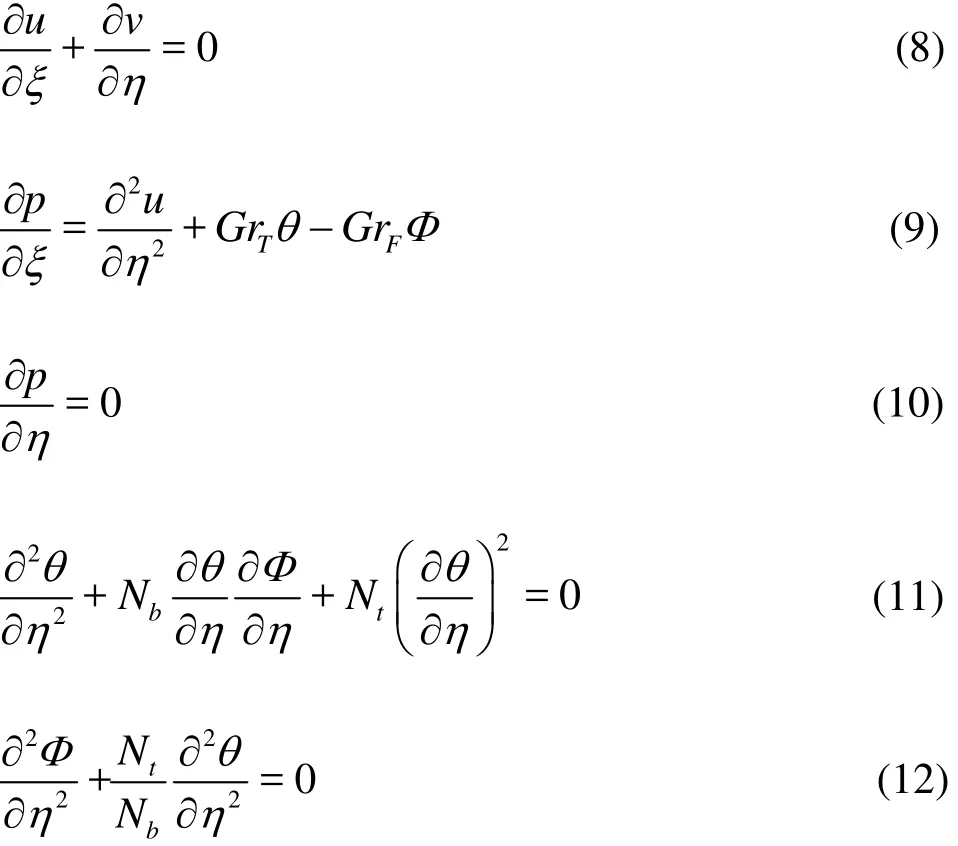
The relevant boundary conditions are specified as follows:

Integrating Eq. (12) twice with respect to η and using the third and fourth boundary conditions of Eq.(13), the nanoparticle fraction (species concentration)field emerges as
we further double integrate Eq. (11) with respect to η. Thereafter we deploy the first and second boundary conditions of Eq. (13) and this generates the solution for temperature field function, as follows

Substituting Eqs. (19), (20) into Eq. (9) we further double integrate the latter with respect to η. Next,we use both boundary conditions (14) and (15), and this leads to an expression for the axial (longitudinal)velocity
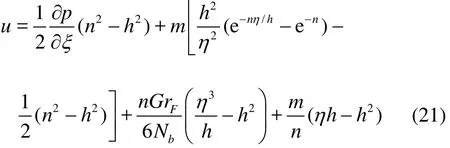
where
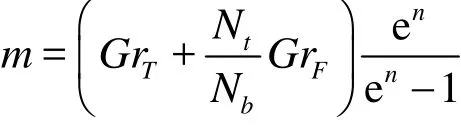
Using Eq. (21) in the mass conservation Eq. (8),integrating with respect to η and also invoking the boundary condition (16), then results in the appropriate expression for transverse velocity which takes the form
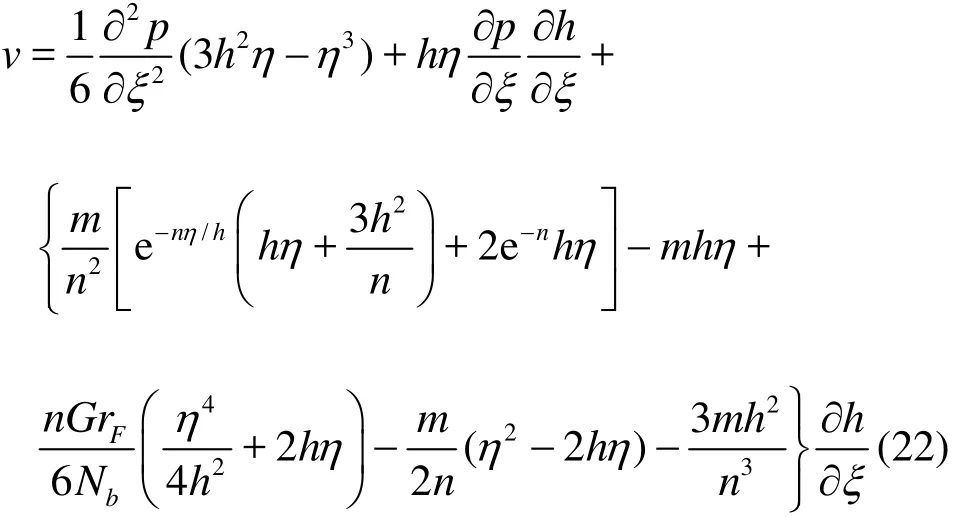
Utilizing boundary condition (17) leads to
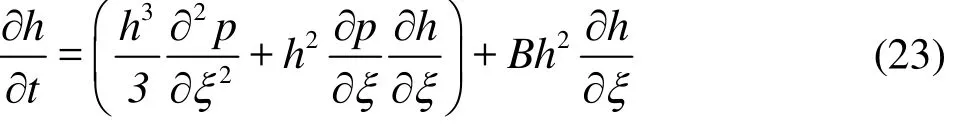
where
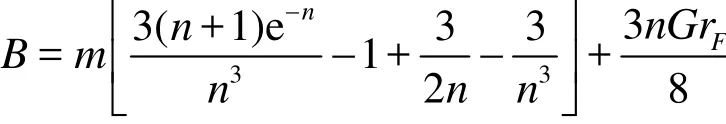
Integrating Eq. (23) with respect to ξ the pressure gradient yields
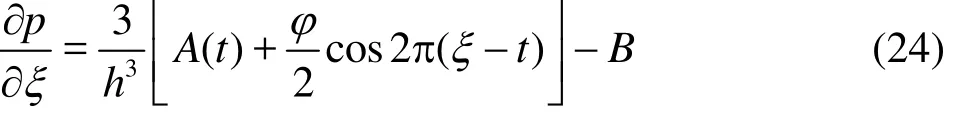
Integrating once again, the pressure difference across the length of channel is evaluated as
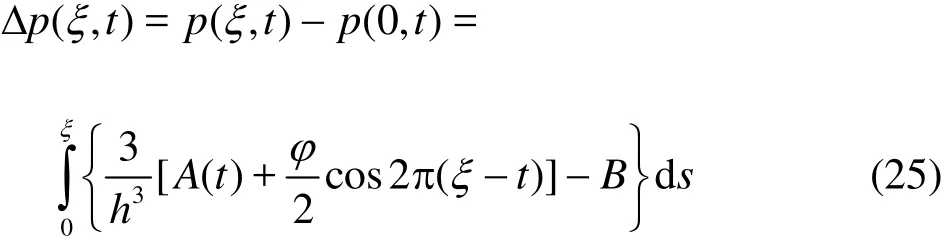
Upon substituting, ξ=l, we arrive at
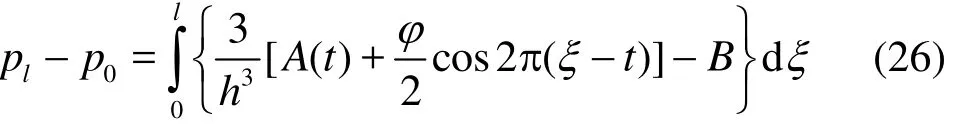
where ()A t is an arbitrary function of time ()t,which is evaluated by a simple manipulation of Eq.(26) and the finite length condition. This leads to

To undertake a parametric study of the effects of the dominant thermophysical and geometric parameters on peristaltic motions, recourse is made to the appropriate integration routines in the symbolic Mathematica software. Visualization of computations is also greatly facilitated with this code and elaborated in due course.
3. Numerical evaluation of results and interpretation
Figures 2-9 illustrate the influence of a range of parameters emerging in the boundary value problem,namely basic-density Grashof numberthermal Grashof number, Brownian motion parameter, thermophoresis parameteron nanofluid temperature, nanoparticle volume fraction, axial velocity and pressure distribution along the length of non-uniform channel. A time cyclic process for bolus(wave) movement has been presented by taking the values of t = 0, 0.25, 0.5, 0.75 and 1.
Figures 2-4 present the effects of α i.e., nonuniformity channel geometry constant on the nanoparticle volume fraction, temperature and axial velocity profiles, respectively. As α increases, the channel becomes wider and more divergent. For the case of, the non-uniform channel retracts to a uniform channel, a case which has already been examined by Tripathi and Bég[17]. In Figs. 2-4, strong thermophoresis and Brownian motion (small particles) are considered via the default values o fFurthermore the plots are for =0.5t i.e., isochrones of the behavior at that instant. With, the thermal and mass (density) buoyancy forces are respectively equal to the viscous hydrodynamic force in the regime. φ (wave amplitude)and δ (wave number) are also prescribed as 0.5 and 2.0 (an even number of peristaltic waves propagate),respectively.

Fig. 2 (Color online) Nanoparticle fraction profiles (Φ(η) vs.η) for various values of α=0, 1, 2 and 3 at φ=0.5,ξ=1, δ=2, t=0.5, N t =1, Nb=1
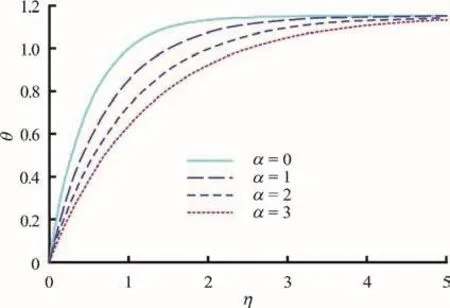
Fig. 3 (Color online) Temperature profiles (θ (η) vs. η) for various values of α=0, 1, 2 and 3 at φ=0.5, ξ=1,δ = 2, t = 0.5, N t =1, N b=1
There is an evident growth in nanoparticle volume fraction with increasing transverse coordinate,whereas the increase in non-uniformity parameter clearly induces a decrease in nanoparticle volume fraction. The greater space available in the diverging channel results in a decrease in intensity of nanoparticles in the regime (Fig. 2), which manifests via weaker concentrations across the channel width.Apparently species diffusion is therefore regulated via divergent channel and this may be useful in achieving better controlled delivery of nano-medicines. Although temperatures (Fig. 3) are also elevated with greater transverse coordinate, as with nanoparticle concentrations (volume fraction) they experience decay with greater divergence in the channel i.e., non-uniformity parameter. However whereas the nanoparticle volume fraction profiles ascend monotonically from zero to attain different maxima at the wall, the temperature profiles exhibit a convergence towards a single peak and plateau at high values of transverse coordinate.Evidently greater non-uniformity of the channel also cools the nanofluid flow across the channel. In Fig. 4,we observe that axial velocity profiles are initially negative indicating some reflux (backflow) at low transverse coordinate values. This trend is eliminated at higher -ηvalues, and the velocity distributions continue to ascend monotonically. The increase in non-uniformity again depresses velocity magnitudes, a feature largely attributable to the destruction in momentum with greater widths of the channel. This behavior is representative of diffuser-type flows in engineering and enables a deceleration in axial flow with judicious selection of the channel wall gradient(angle of divergence).
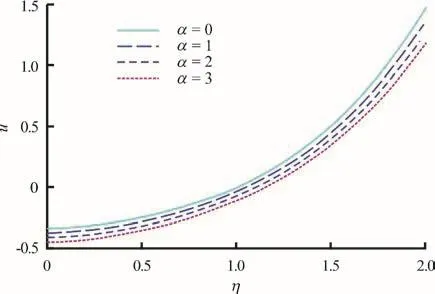
Fig. 4 (Color online) Ax ial veloc ity pro fi les (u(η) vs. η) for various values ofα=0,1,2,3atφ=0.5,ξ=1,∂p/∂ ξ=1, δ=2, t=0.5, N t =1, N b =1, G rT=1, G rF=1
Figures 5(a)-5(e) presents the effects of geometric, nanofluid and buoyancy parameters on transverse velocity profiles. In all these plots the peak transverse velocity generally arises in the vicinity of the centerline of the channel, although the distributions are skewed parabolas. In Fig. 5(a) the transverse velocity is observed to be enhanced with greater non-uniformity parameter. The destruction of axial momentum results in a concomitant boost in transverse momentum as the channel diverges.
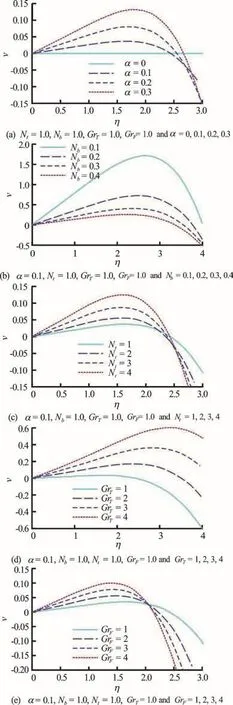
Fig.5 (Color online) Transverse velocity profiles (v(η) vs. η)at φ=0.5, ξ=1, ∂p/∂ξ=1, δ=2, t=0.5
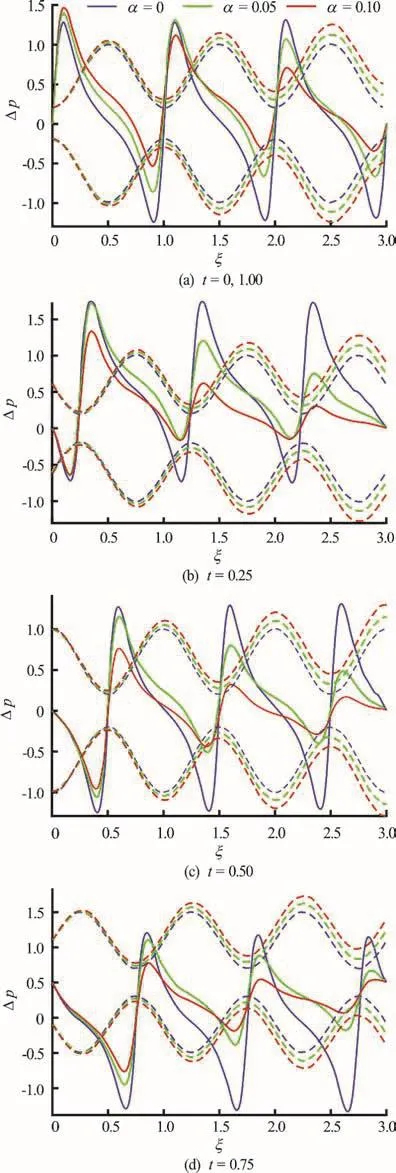
Fig.6 (Color online) Pre ssure dif ference vs. axia l distance for α=0(unif ormchanne l)α= 0.05,0.1 (no n -uniform channel)andφ=0.8,δ=1,N t =1,N b =0.1,GrF =0.1, G rT =1,pl = p 0 =0, l = 3 at various instants. Dotted color lines represent the position of wave and color solid lines show pressure distribution along the length of channel
This accelerates flow across the channel but decelerates it along the channel. With increasing Brownian motion parameter,bN, (Fig. 5(b)), the transverse velocity is markedly suppressed, across the width of the channel. Figure 5(c) demonstrates that with an increase in thermophoretic parameter,tN, the transverse velocity is elevated strongly. Thermophoresis physically is the transport of nano-particles in the direction of a decreasing temperature gradient. The net force acting in the opposite direction to the temperature gradient, i.e., towards the low temperature region is produced via differential bombardment of nanoparticles which originate from the relatively hot and cold regions in the vicinity of particles. This effect manifestly influences momentum diffusion.Figs. 5(d), 5(e) illustrate that with increasing thermal and mass (density) Grashof number the transverse velocity is accelerated significantly.
Figures 6(a)-6(e) depict the collective influence of time ()t and non-uniformity parameter ()α on axial pressure difference distributions. Pressure difference ()pΔ, is generally accentuated with increasing α (channel non-uniformity parameter). The periodic nature of the pressure distributions is clearly captured in these figures. With longer time, the amplitude of pressure difference is observed to be markedly depressed (Fig. 6(d)) compared with smaller time elapses. At large time the pressure difference for a uniform channel is considerably lower than for small times, and is in addition lowest for a uniform channel–whereas in Figs. 6(a)-6(c) the maximum pressure difference (at lower times) corresponds to uniform channels.
Figures 7(a)-7(e) depict the collective influence of time (t) and Brownian motion parameteron axial pressure difference profiles. Increasing Brownian motion is found to enhance pressure difference magnitudes i.e. smaller nano-particles induce greater pressures in the peristaltic flow regime. Increasing time is also seen to considerably boost pressure differences (Figs. 7(a), 7(e)) have the highest pressure peaks compared with lower peaks in intermediate time plots.
Figures 8(a), 8(b) present the combined influence of time (t) and thermophoresis parameteron axial pressure difference profiles. Increasingvalues clearly result in a suppression of pressure differences along the channel length. With progression in time, a generally more even distribution in pressure differences is observed. Evidently stronger migration of particles away from the directi on o f i ncreasing temperature gradient contributes to adropinpressure difference in the peristaltic propulsion.
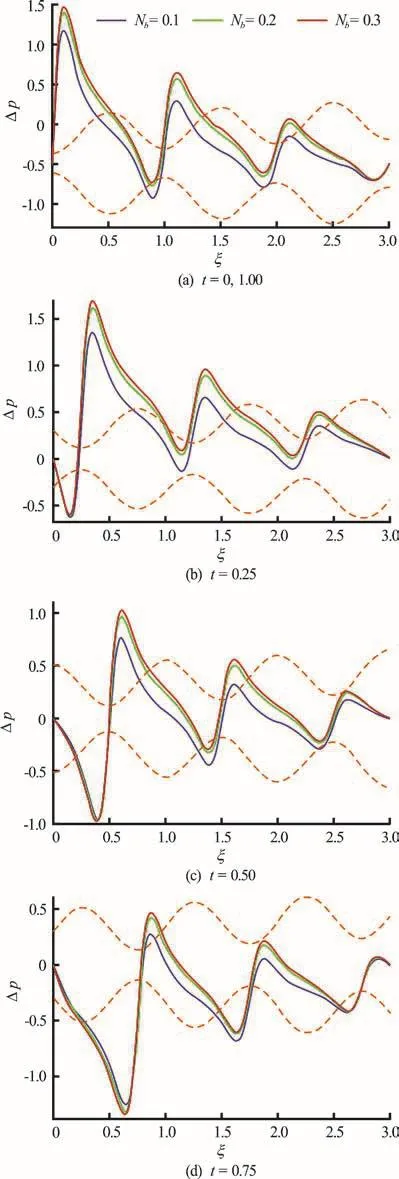
Fig.7 (Color online) Pressure difference vs. axial distan ce for Nb =0.1, 0.2, 0.3 and α=0.1, φ=0.8, δ=1,Nt =1, δ=1, N t =1, G rF =0.1, G rT =1,pl = p 0 =0,l = 3 at various instants. Dotted color lines represent the position of wave and color solid lines show pressure distribution along the length of channel
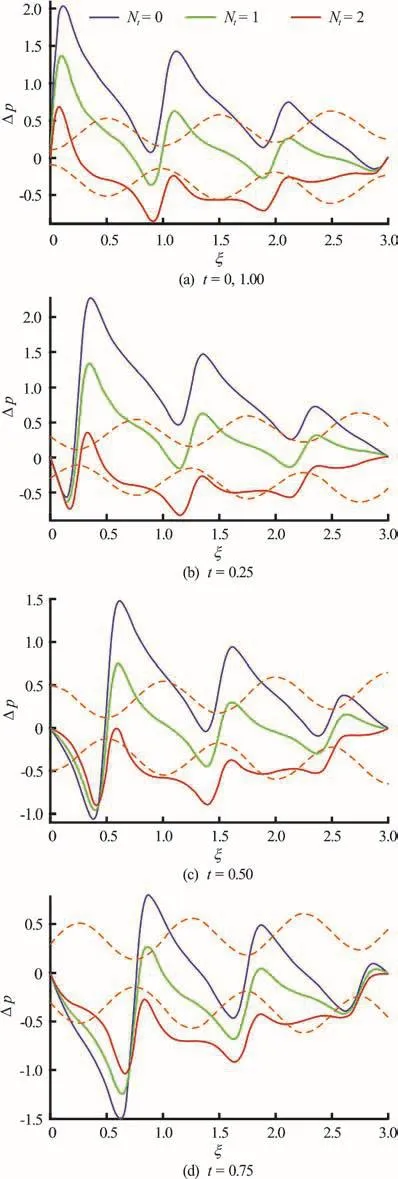
Fig.8 (Color on lin e) Pressure difference v s. axial distance for Nt =0,1,2and α=0.1, φ=0.8,δ=1,N b =0.1,GrF =0.1, G rT =1, p l = p0 =0, l = 3 at various instants. Dotte d colo r lines represent the position o f wave and colorsolidlinesshowpressuredistributionalongthe length of channel
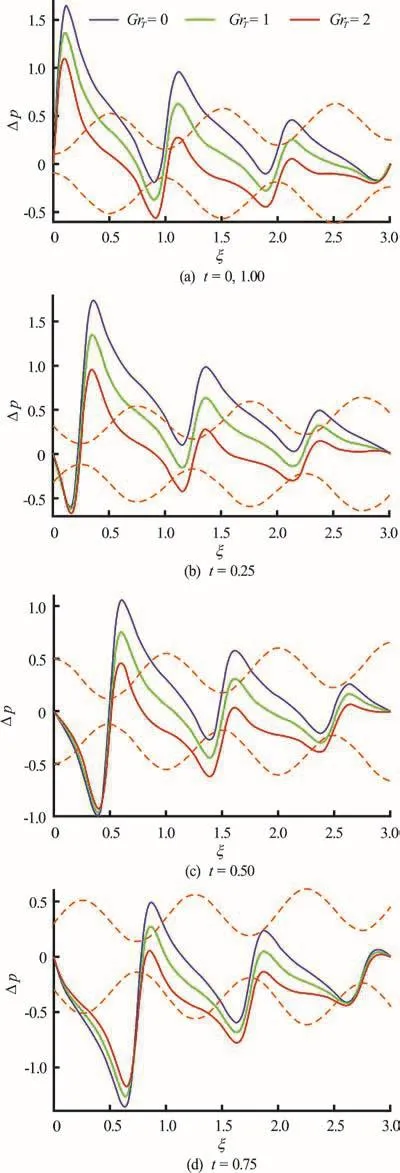
Fig.9 (Color o nli ne ) Pressure difference vs. axial distance for GrT =0,1,2and α=0.1, φ=0.8, δ=1, N b =0.1,N t =1, G rF =0.1, pl = p 0 =0, l = 3 at various instants. Dotte d colo r lines represent the position of wave and colorsolidlinesshowpressuredistributionalongthe length of channel
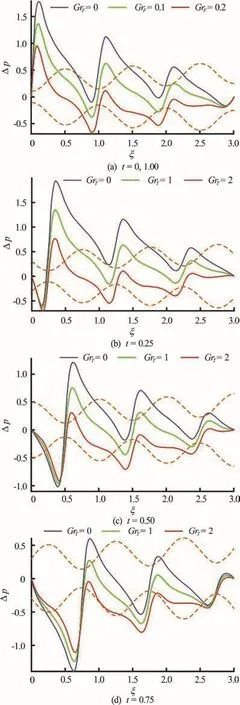
Fig.10 (Color online) Pressure difference vs. axial distance for GrF =0, 0.1, 0.2 and α=0.1, φ=0.8, δ=1, Nb=0.1, G rT =1 , pl = p 0 =0, l = 3 at va rio us ins tants.Dotte dcolo rline srepr esentthe positionof wave and colorsolidlinesshowpressuredistributionalongthe length of channel
Figures 9(a)-9(d) depict the combined effects of time (t) and thermal Grashof numberon axial pressure difference profiles. IncreasingTGr which implies greater thermal buoyancy relative to viscous force, induces a reduction in pressure difference across the channel length. With increase in time there is a distinct evolution in pressure profiles,with peak pressure difference at very low and very high times (Figs. 9(a), 9(d)) migrating for intermediate values of time.
Figures 10(a)-10(d) show that although the same general effect is generated on pressure difference-axial coordinate plots with an increase in mass (density)Grashof number, the increase inFGr required is an order of magnitude less than for thermal Grashof number. The pressure difference profiles are modified with time, with peaks migrating. However the overwhelming influence of mass diffusion (nanoparticles)on pressure evolution compared with thermal buoyancy is evident.
4. Conclusion
Analytical solutions have been developed for the peristaltic flow, heat and mass transfer of a nanofluid in a non-uniform channel, as a simulation of nanomedical peristaltic micro-pumps, using a robust model for Brownian motion and thermophoresis. The nondimensional solutions have been evaluated via Mathematica symbolic software. Computations have shown that increasing thermophoresis effect accelerates transverse flow whereas it depresses pressure differences. Increasing thermal and mass Grashof number both serve to suppress pressure differences,whereas the latter achieves a greater effect for small increments. Pressure difference is also enhanced with greater Brownian motion effects. Axial velocity,nanoparticle volume fraction (species concentration)and temperatures are all decreased with greater divergence of the channel geometry i.e., non-uniformity parameter. The present model has been restricted to Newtonian formulations for the nanofluid shear stress-strain characteristics. Future work will explore non-Newtonian nanofluids (e.g., power-law) and microstructural Eringen models[29-30], which are more representative of certain linctus solutions, medical creams and ophthalmic agents and work in this direction is in progress.
Acknowledgement
The authors are grateful to the reviewers for their comments which have served to improve the present work.
杂志排行
水动力学研究与进展 B辑的其它文章
- Call For Papers The 3rd International Symposium of Cavitation and Multiphase Flow
- An integral calculation approach for numerical simulation of cavitating flow around a marine propeller behind the ship hull *
- Numerical study on influence of structural vibration on cavitating flow around axisymmetric slender body *
- An integrated optimization design of a fishing ship hullform at different speeds *
- Critical velocities for local scour around twin piers in tandem *
- Dynamic analysis of wave slamming on plate with elastic support *
