RSS室内定位信号经验模型重构研究
2019-01-05薛卫星花向红李清泉邱卫宁
薛卫星,花向红,李清泉,邱卫宁
(1.武汉大学 测绘学院,湖北 武汉,430079;2.武汉大学 灾害监测与防治研究中心,湖北 武汉 430079;3.深圳大学 空间信息智能感知与服务深圳市重点实验室,广东 深圳 518060)
随着信息技术的迅猛发展,室内定位技术得到快速发展。在各种室内定位技术中,基于RSS(基于接收信号强度定位技术)[1]的定位方法因成本低廉、覆盖面广泛和无需添加任何硬件设备[2]等优点,已经成为室内定位的主流定位方法。位置指纹数据库的建立是Wi-Fi室内导航定位系统的重要方面,主要有离线阶段采集指纹参考点RSS样本建立位置指纹数据库和采用传播模型法建立数据预测数据库两种方法。离线阶段建立参考点RSS位置指纹数据库采用几何布网的方法,类似于控制网的建立与加密;传播模型法建立数据预测数据库则是采用一部分参考点的RSS样本建立传播模型,再用该传播模型进行剩余参考点RSS样本的预测,从而建立实测数据和预测数据相结合的指纹数据库。
本文在RSS几何空间特征点构建指纹库的精度分析和RSS欧氏空间信号特征点信号模型重构的精度分析的基础上,对不同类型的特征点赋予不同的权值,并利用低秩矩阵填充理论,提出了RSS室内定位信号经验模型的重构算法。给出了RSS室内定位信号经验模型重构的步骤,通过实验说明了算法的可行性。
1 低秩矩阵填充理论
根据信号重构的经典定律奈奎斯特采样定理[3],利用信号采样值信号重构时,信号的采样率至少应该达到信号带宽的2倍以上,才能实现信号的逼真重构。近些年来,Candes[4]与Donoho D L[5]等人相继提出完善的压缩传感技术,逐渐成为图像处理和信号处理等方面的研究热点。压缩传感技术通过测量矩阵的转换理论,将高维空间的稀疏信号进行压缩进而投影到一个低维空间上;再通过该信号的稀疏性或可压缩性,从而降低信号采样的数据量,同时通过某些信号重构的算法再准确地重新构造出信号的真实分布情况。稀疏性是指矩阵中的大部分元素的数值为0,而数值不为0的元素的个数相对比较少[6-14]。
低秩矩阵填充理论是基于压缩传感技术的,主要解决如何在稀疏的误差中恢复填充出低秩矩阵的问题。矩阵的低秩性是指矩阵的秩远远小于矩阵的行数和列数[15]。假设目标定位区域是一个m×n个指纹点进行数据采样的矩形区域,则每个AP都将会形成一个信号强度m×n的采样矩阵。传统的位置指纹定位法是在每个指纹点上进行RSS数据采样测量,但是这样采样的工作量很大;假设只采集一个小规模的采样点子集,那么就需要用低秩矩阵填充理论来重新构造出整个目标定位区域的二维矩阵。圆圈点上进行了实际数据采样测量的位置指纹采样点,其他区域需要我们用低秩矩阵填充理论来填充,如图1所示。

图1 采样示意图
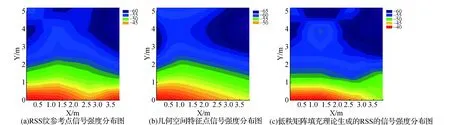
把目标定位区域的某个AP源的信号强度RSS采样数据定义为矩阵X,所有采样格网点的个数N即该矩阵的元素个数N;但是在实际采样时,只测量目标定位区域随机选择的s(s 因为希望实际采集数据的工作量降低,即指纹点越少越好,这就要用到仿射矩阵秩最小化的理论,即 s.t.A(X)=b. (1) s.t.A(X)=b. (2) 如何使得(2)的解是(1)的解,Recht B等,给出了以下条件[16]: 假设1≤r≤m≤n,秩为r的矩阵X0满足参数为μ的并且只与矩阵X0的奇异值向量相关的强非相干条件,如果观测元素位置是随机均匀分布的s个采样点,那么存在一个正的常数C,使当 s≥Cμ4n(logn)2, (3) 时,矩阵X0至少以1-n-3概率收敛为以上优化问题的唯一确定解。所以,采用核范数最小化的理论将原始的组合优化问题转化为用这种凸松弛的优化问题,能够以非常高的概率来精确地填充出矩阵b的所有元素。 然后,结合奇异值分解的算法和矩阵填充的贪婪追踪算法[17]介绍低秩矩阵填充的具体方法。首先,将矩阵X通过奇异值分解[18]分为如式(4)所示的3个矩阵: X=UΣVT. (4) 其中,U是一个m×m的正交矩阵,Σ=diag(σ1,…,σr)是一个m×n的半正定对角矩阵,VT是矩阵V的共轭转置矩阵,是n×n阶的正交矩阵。令L=UΣ1/2,R=VΣ1/2,则式(4)可以分解为X=UΣVT=LRT,代入式(1)得: min rank(LRT), s.t.A(LRT)=b. (5) 设r0为矩阵X秩的预估计值,矩阵L的阶为m×r0,矩阵R的阶为n×r0。考虑的矩阵L和R的具有多解性,采用Frobenius范数[19]最小化来优化控制,即: s.t.A(LRT)=b. (6) 另外,由于RSS采样数据中可能含有误差以及定位区域中的矩阵可能不完全符合低秩性,将最小化模型约束条件变换成为非约束模型: (7) 然后,需要通过交替迭代过程推导出矩阵L和R:首先,通过虚拟AP技术的传播模型法列方程,利用最小二乘法计算出矩阵X的初始值X0,进而推算出其秩的预估值r0和矩阵X的可能分解矩阵,随机选取矩阵X的一组分解矩阵作为矩阵L和R的初始值;其次,固定矩阵L,利用最小二乘法优化矩阵R;然后,更新并固定矩阵R,同样利用最小二乘法优化矩阵L;多次重复以上交替迭代过程,直至按式(7)计算的目标函数收敛,并达到设定的函数误差阈值:最后迭代的结果与倒数第二次迭代的结果之差除以最后迭代的结果的数值的绝对值小于等于0.000 1。 在RSS室内定位信号经验模型重构的过程中,用到RSS的欧氏空间信号特征点和几何空间特征点两种特性的点。RSS的欧氏空间信号特征点需要根据室内空间的具体情况确定,RSS的几何空间特征点需要在少量RSS数据采集的基础上,利用低秩矩阵填充理论计算出其所有的几何空间特征点。 几何空间特征点填充后,采样点的原始数据和重构数据会产生一定的误差,计算出该误差。数据选择时,已经有数据采样的几何空间特征点的数据采用原始采样数据,新填充的数据则根据所计算出的误差赋予相应的权值。然后,利用RSS的欧氏空间信号特征点、由采样数据的几何空间特征点和加权的新填充的几何空间特征点进行RSS室内定位信号经验模型的重构。模型重构的具体流程如图2所示。 图2 RSS室内定位信号经验模型重构算法流程 图3 实验点位分布示意图 为了考察基于信号的欧氏空间信号特征点和几何空间特征点的RSS室内定位信号经验模型的定位效果,在武汉大学测绘学院101机房进行了模型定位实验,如图3所示。图3中,机房101有6个AP,定位区域为3.9 m×5.2 m,相邻两个采样点间的距离为0.65 m(即最小格网为0.65 m×0.65 m的方形区域),○代表数据采样的网格点,共有63个采样网格点。实验时,采用1S的采样率,每个时段采集数据3 min。由于不同手机接收AP信号强度具有差异性,故实验中所有数据的采集均采用同一个手机进行。 实验中,采用1.3 m×1.3 m的格网点作为位置指纹定位法的指纹参考点,用于构建指纹定位离线阶段的指纹数据库;根据信号重构的奈奎斯特采样定理,采用0.65 m×0.65 m的格网点作为信号模型重构的参考真实值。 根据信号重构的奈奎斯特采样定理,将0.65 m×0.65 m格网点作为信号模型重构的参考真实值,以AP1为例,其形成的原始信号强度分布图显示在图4(a)中。 图4 信号强度分布图 从图4中可以看出,每个AP的RSS分布图中都存在信号强度突变点,也就是说,试验采样数据中可能含有粗差。因此,首先需要结合实验具体情况剔除这些粗差采样点,主要指非边界处的信号强度突变点,而边界处的信号强度突变点则更可能是由Wi-Fi信号的多径传播造成的。具体粗差采样点的剔除情况见表1。剔除粗差采样点后,以AP1为例,RSS信号分布图如图4(b)所示。 表1 不同AP的粗差剔除数目及其数据删除率 从图4(b)中可以看出,剔除极少数的粗差采样点后,RSS信号分布图的质量得到优化;然后,从图4(b)中选取RSS的欧氏空间信号特征点,根据每个AP信号分布图各自的特点,选取的欧氏空间信号特征点的个数不同,具体数目情况和占总点数的百分比见表2;最后,用选取的特征点来重新构造信号模型,重构结果如图4(c)所示。 从图4c中可以看出,只需利用总数据25%左右的RSS欧氏空间信号特征点的数据,就可以基本勾勒出RSS的信号分布图。但是,由于只选取了RSS欧氏空间信号特征点的部分数据,没有加入RSS的几何控制点(即RSS几何空间信号特征点)的数据,所以勾勒出RSS的信号分布图并不能与参考真实值的RSS信号分布图完全吻合。 表2 不同AP选取的欧氏空间信号特征点数目及其比例 在室内位置指纹定位离线构建指纹数据库阶段,采用1.3 m×1.3 m的格网点,其指纹参考点的信号强度分布图如图5(a)所示。从图5(a)与图4(b)的对比中,可以看出:由1.3 m×1.3 m格网采样数据所形成信号强度分布图与0.65 m×0.65 m格网形成信号强度分布图的轮廓大致相同;但是1.3 m×1.3 m格网勾勒出RSS信号分布图的很多细部RSS重构值并不理想,与0.65 m×0.65 m格网的采样值相差较大。所以,仅仅采用RSS的信号几何空间特征点进行RSS信号强度分布图重构的效果是不太理想的。 从1.3 m×1.3 m格网点的信号强度分布图中,随机均匀选取RSS的几何空间特征点(10个),保证每行每列都有采样数据。首先,利用这些选取的数据直接生成信号强度分布模型,如图5(b)所示。然后,利用低秩矩阵填充理论和虚拟AP技术重新构造信号强度分布模型,RSS信号强度分布图重构结果如图5(c)所示。 图5 信号强度分布图对比 从图5(c)与图5(a)、图5(b)的比较中可以看出:图5(c)与图5(a)的相似度大于图5(b)与图5(a)的相似度,所以利用低秩矩阵填充理论生成的RSS信号强度分布模型比利用原始选取的RSS几何空间特征点生成的信号强度分布模型的精度高。另外,图5(c)中某些AP的RSS信号分布图中有个别的突变点,说明利用低秩矩阵填充理论生成的RSS数据对选取的RSS几何空间特征点数据有一定的依赖性。所以,在进行RSS几何空间特征点的数据选取时,既要保证RSS的突变点的剔除,又要保证选取数据的随机性。 为了便于分析比较,首先将RSS几何空间特征点和RSS欧氏空间信号特征点的详细采样情况列在表3中。然后,利用这些特征点生成原始RSS所有特征点生成的信号强度分布模型,如图6(a)所示。最后,再将加权后的RSS几何填充数据、RSS几何空间特征点和RSS欧氏空间信号特征点结合,生成RSS室内定位信号经验模型重构的信号强度分布模型,如图6(b)所示。 表3 不同AP特征点数目及其比例 图6 原始RSS所有特征点和RSS室内定位重构信号强度分布 从图4(b)、图5(a)、图6(a)和图6(b)的相互比较中,可以看出:图6(b)与图5(c)的相似度高于图6(a)与图4(b)的相似度,明显高于图5(a)与图4(b)的相似度。所以,利用低秩矩阵填充理论和虚拟AP技术生成的RSS室内定位信号经验模型重构的信号强度分布模型的定位精度较高。 最后,计算RSS室内定位信号经验模型的定位误差。本次实验中,经典指纹定位算法与RSS经验模型的数据采样量如表4所示。每个AP有63(7×9)个数据,除去少数突变点,基本保证每个AP都有60个左右的数据量,共有360个左右。定位精度分析时,用重构的RSS与实际采样的RSS来根据传播模型计算他们之间的距离差值,从而计算出该经验模型的定位误差,具体误差分析如表5所示。 从表4和表5中可以看出,在数据采样量略高于位置指纹(约为1.37倍)的情况下,利用RSS室内定位信号经验模型的定位精度显著高于位置指纹的定位精度(约为2倍),特别是0.5 m以内的定位精度。所以,在考虑RSS欧氏空间信号特征点的基础上,利用低秩矩阵填充理论重构出RSS室内定位信号的经验模型具有一定的应用前景。 表4 指纹定位算法与RSS经验模型的数据采样量 表5 RSS室内定位信号经验模型的定位误差分析 % 本文在详细介绍低秩矩阵填充理论的基础上,提出了RSS室内定位信号经验模型的重构算法。借鉴地形图中地类特征点和地类特征线概念,提出RSS欧氏空间信号特征点、特征线的概念,并在RSS几何空间特征点构建指纹库的精度分析和RSS欧氏空间信号特征点信号模型重构的精度分析基础上,对不同类型的特征点赋予不同的权值,用于RSS室内定位信号经验模型的重构。并通过与经典指纹位置定位算法的实验对比分析中,说明了RSS室内定位信号经验模型的精度和可行性。
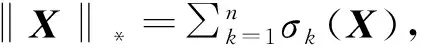
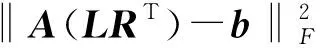
2 RSS室内定位信号经验模型的重构

3 实验及结果分析
3.1 实验方案

3.2 欧氏空间信号特征点信号的模型重构



3.3 几何空间特征点构建指纹数据库
3.4 RSS室内定位信号经验模型重构结果的分析与比较




4 结 语
