基于TLS的盾构隧道收敛测量研究

曹 震，史玉峰

(南京林业大学 土木工程学院,江苏 南京 210037)

地铁隧道主体结构施工完毕后，由于受到地面、周边建筑物负载、土体扰动、隧道周边工程施工及隧道工程结构施工等原因，会对隧道产生综合影响而造成隧道变形，产生收敛。为保证隧道安全和铺轨的顺利进行，需要对隧道的收敛情况进行准确测量。

通常盾构隧道监测采用布置一系列离散的监测点的形式，借助全站仪、收敛计仪器设备，对监测点坐标和隧道拱顶沉降及隧道内壁收敛进行监测。随着地面激光扫描(Terrestrial laser scanning，TLS)技术的发展与普及，TLS在许多领域得到应用。TLS是一种新兴测绘技术，它能够快速扫描并记录被扫描物体表面的信息，通过一个个激光点记录表面信息，这些数据称为点云数据。TLS已经在逆向工程、机械设计领域、路桥隧道和水利工程等领域有着广泛应用[1-5]。近些年，一些学者和研究人员对点云数据特征提取、点云数据配准、点云数据建模和基于点云的几何断面提取等方面展开了研究[7-12]，取得了一些研究成果。

本文将研究TLS在盾构隧道收敛测量中的应用，包括点云数据采集、点云数据预处理、隧道断面截取等。

1 点云数据获取

盾构隧道数据采集包括：基准点布设与测量、隧道内壁数据采集。布设基准点是为了将隧道内壁点云坐标转换到施工坐标系下。基准点通常布设在没有变形或变形较小区域，沿隧道走向均匀分布[13]。一般采用高精度全站仪或测量机器人准确测量基准点坐标。

隧道是超长线状结构，需要布设多站才能完成整条隧道的测量工作。为保证扫描数据质量，需要依据采集设备参数、隧道直径确定测站间距和扫描分辨率。设站的测站间距与扫描范围内的最大入射角和隧道的直径有关，入射角与测站间距的关系为[1]

(1)

式(1)中，θ为测站扫描激光的入射角，S为测站间距，m，D为隧道内径，m。一般地，当入射角大于65°时误差开始急剧上升[14]，故选择θmax=65°，有S=2.1D。

点云数据扫描质量与式(1)中的θmax、S有关，最佳扫描分辨率由式(2)确定。

(2)

2 点云数据预处理

2.1 点云滤波

点云数据采集过程中不可避免地受到外界因素的影响，可能产生一些噪声点。为保证重构模型的准确性，需要消去这些噪声点。本文采用拟合二次曲面与多面函数结合的方法进行滤波[11]，先用二次曲面拟合获取点云的大致趋势面去掉较大误差点，同时为多面函数拟合提供精度较高的可选拟合点，然后对选取的点进行多面函数拟合及平差模型的解算，实现隧道的点云滤波。二次曲面拟合模型[17]：

(3)

式中：α0、α1、α2、α3、α4、α5为二次曲面拟合系数，(xk,yk,zk)为拟合点云的三维坐标。

当拟合点数m大于必要观测点数，根据其误差方程利用最小二乘法求得α0、α1、α2、α3、α4、α5的值。

多面函数拟合的原理[18]：设扫描区域有m个已测点s(x,y)或记为数据点(x,y,z)，si为点(xi,yi)上的观测量，用n个核函数的总和去逼近函数s(x,y)，即

s(x,y)=∑αj×θ(x,y,xj,yj).

(4)

式中：θ(x,y,xj,yj)为所选取的核函数，αj为待定系数。将方程列成矩阵的形式，利用最小二乘法可求得系数αj的值。最后通过求点到面的距离设定阈值，将噪声点去除。

2.2 点云配准

点云配准是通过计算两相邻测站点云数据所在坐标系之间的转换参数，将所有点云统一到同一个坐标系下。点云配准常采用转换参数方法。常用的参数计算方法是以9个方向余弦参数(3个独立参数，6个非独立参数)和3个平移参数为待求参数[7]。当控制点数为n时，得到3n个误差方程和6个条件方程，建立附有限制条件的高斯-马尔科夫模型(G-M模型)，采用附有限制条件的间接平差法对误差方程进行求解。本文采用约束总体二乘的方法解算参数[7]。其限制条件的模型为

(5)

式中，y为观测向量，ey为观测值的随机误差向量，A为系数矩阵，EA为系数矩阵A的随机误差矩阵，ξ0为参数初值向量，δξ为参数改正数，ξ为参数估计值，B、wx为条件方程系数和常数项。

约束总体最小二乘估计准则为

(6)

经迭代法解算得旋转参数ξ。

3 隧道断面提取

3.1 提取隧道中轴线

经过点云去噪和点云配准，采集的隧道点云数据已经转换至施工坐标系下。隧道中轴线贯穿于隧道各环圆心，是一条虚拟的空间曲线。中轴线不仅反映了隧道沉降和偏移情况，还可以为隧道断面截取提供隧道的空间姿态信息[12]，保证所截取的断面是隧道的横断面。中轴线拟合是地铁隧道收敛测量中关键。因隧道表面并不是光滑的，加之仪器产生的噪声点以及隧道内未完全剔除的噪声点的影响，隧道中轴线不能直接应用最小二乘方法进行拟合。

本文采用Ransac算法进行轴线拟合，先将点云投影到两个平面内，然后分别在两个平面内实现二维的边界提取、边界拟合以及中线拟合。具体提取步骤如下：将点云数据分别投影到xoy与yoz面内，对点云数据进行网格化[4]，单元网格大小为隧道投影后宽度的1/20；若单元格内有点则矩阵Nij=1(如图1(a));若单元格内没有点则矩阵Nij=0(如图1(b))；然后用其周围其他8个单元判断其是否为边界点，判断式为

(7)

对于边界单元，对其内的点坐标求取平均值作为边界点。

图1 矩阵N

采用Ransac算法[16]以及二次曲线方程拟合出边界线，即从边界点中任意先取出3个点计算出二次曲线方程的系数，计算其他点到该曲线的距离，若距离小于阈值则归为局内点，计算出局内点的个数，这样进行N次计算，取局内点最多的一次并用其局内点进行最小二乘拟合得到二次曲线方程。

二次曲线方程：

(8)

式中，a0、a1、a2、b0、b1、b2为方程系数。

取一条边上的一点，求出该点法线与另一条边的交点，算出两点的中点，重复操作可得一系列中点。同理在另一条面内求出中点，采用Ransac算法将中点进行二次曲线拟合，得到中轴线方程。提取XOY平面、YOZ平面的中轴线。

3.2 断面截取与拟合

设隧道中轴线上一点p，其坐标为(xp,yp,zp)，若该点位于隧道直线段，以中线为法线，过该点计算其平面方程；若该点位于隧道曲线段，由式(8)可知该点轴线方程为

则垂直于p点切线的平面方程可表示为[15]

(9)

设点云断面厚度为d，则截取的断面点集Q为

截取的隧道断面点是由点云(x,y,z)组成的集合，通过旋转矩阵可将其旋转至法线与其中一条坐标轴相平行的方向，这样就将三维坐标转换成二维。其计算方法如下：

旋转矩阵

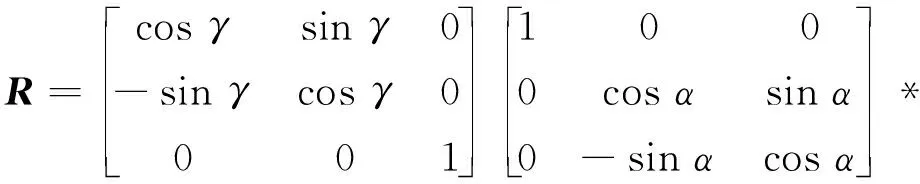
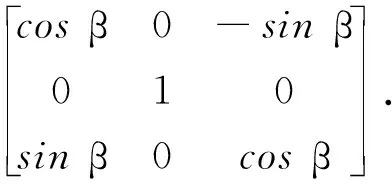
(10)

设断面点集为Q，转换后的点集为Q′

则Q′=R*Q

盾构隧道断面点云模型采用椭圆方程进行拟合，其椭圆方程为：

(t为参数)

(11)

线性化后为：

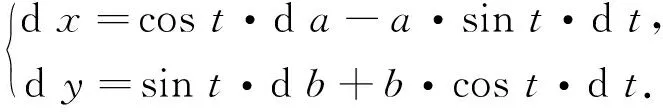
(12)

由最小二乘法可求出系数a，b、c1、c2，即得到椭圆方程。

3.3 收敛数值计算

取过椭圆中心的直线：

y=tanγ·x+c.

(13)

式中，γ为选取的角度，c=c1-c2。

联立椭圆方程(11)，有

(14)

其中，a、b、c1、c2经过拟合已求出。

根据选取的不同角度γ，求出直线与椭圆在各方向上的交点(xγ,yγ)，则可得收敛半径：

(15)

4 试验分析

本文选择某市地铁1号线某段隧道(长度约400 m)作为研究区。研究区内基准点采用Leica TM30全站仪采集其三维坐标，隧道内壁数据采集由Faro focus 3D地面激光扫描仪完成。

点云数据配准及滤波基于Faro Scene完成，如图2、图3为配准后点云，图4为去噪前、后的点云。

图2 点云配准

图3 点云配准局部

图4 去噪前后点云

隧道断面数据处理按3.1节中所述算法提取出隧道中心轴线，提取的YOZ面轴线如图5所示，(横轴为Y轴 ,纵轴为Z轴)。提取的XOY面轴线如图6所示(横轴为Y轴 ,纵轴为X轴)。

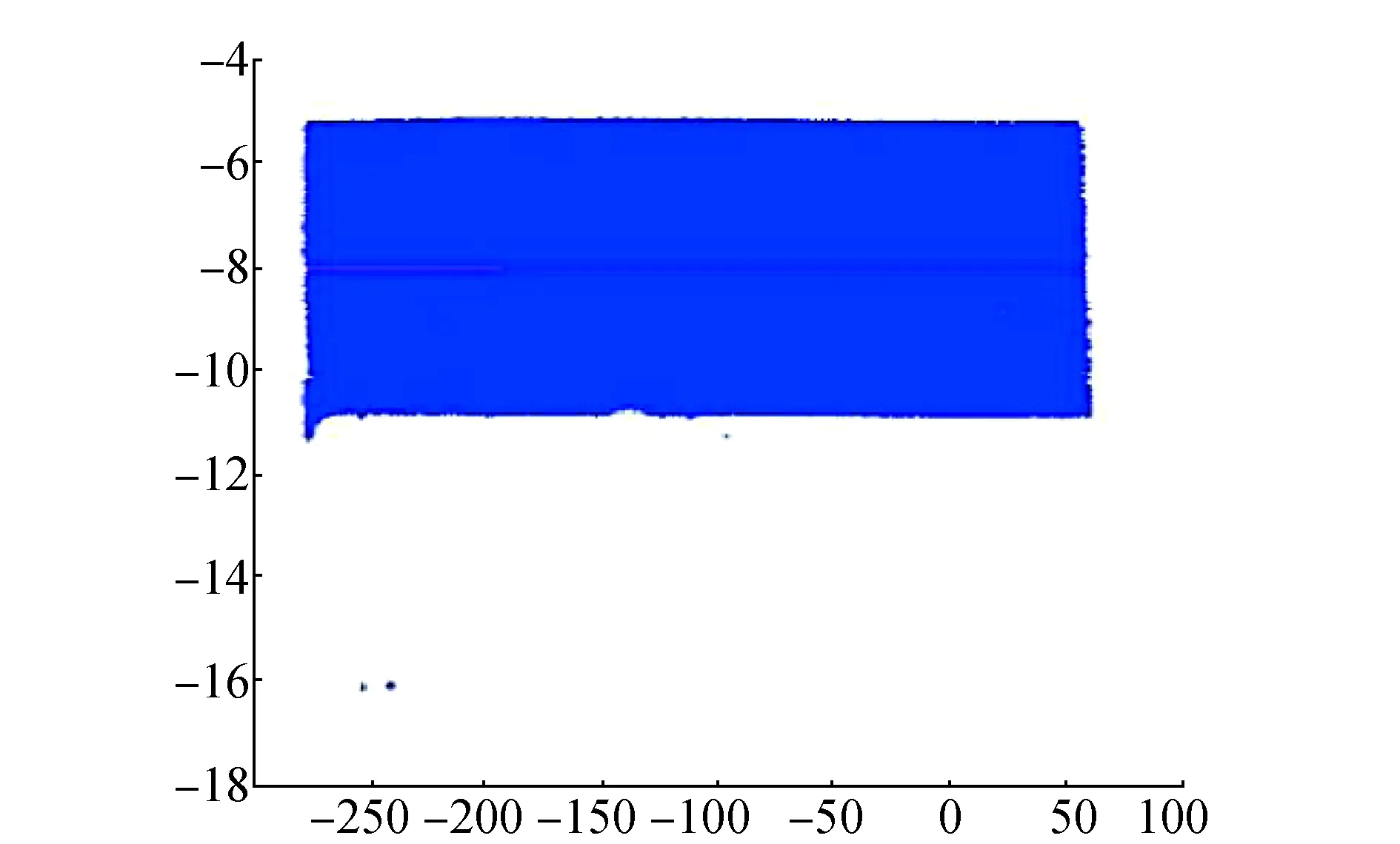
图5 YOZ中轴线(单位：m)

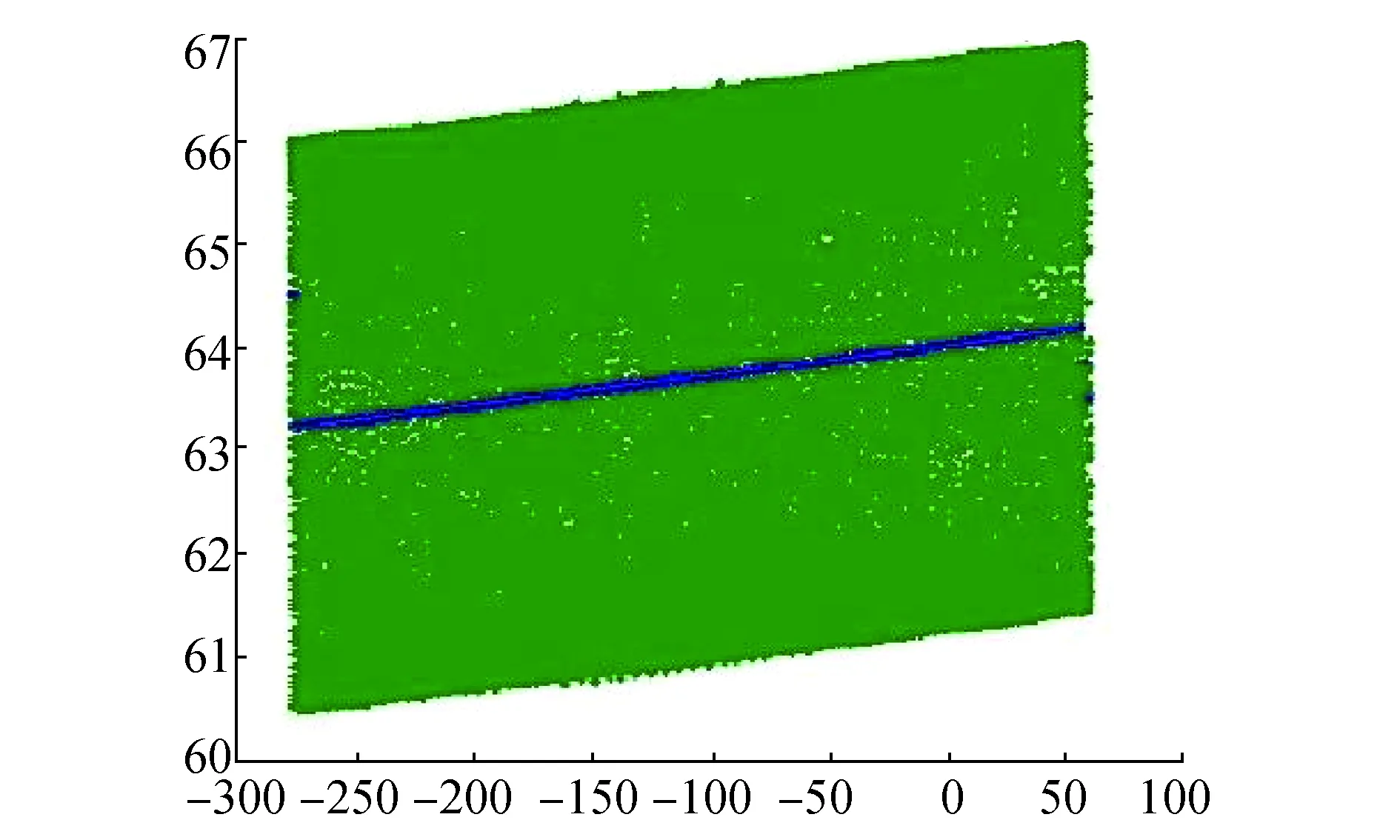
图6 XOY面中轴线(单位：m)

从隧道起始端点开始，每隔10 m截取一个断面，所截取的截面厚度设置为2 mm(如图7所示)。截取断面点之后对其进行旋转并采用椭圆方程进行拟合，分别求出0°、45°、90°、135°、180°、225°、270°和315°方向上的收敛半径，如图8所示(横轴为X轴，纵轴为Y轴)。

图7 连续隧道断面(单位：m)

图8 拟合隧道断面(单位：m)

5 结语

本文分析研究了地面激光扫描在盾构隧道收敛测量中的应用，从数据采集、数据预处理、点云模型构建和收敛值测算等方面展开研究，并实例分析验证了上述方法的有效性。