破碎煤体再造矩形通道受力分析*

郝传波，张 睿，成乾龙，肖福坤，王厚然

(1. 黑龙江科技大学，黑龙江 哈尔滨150027；2.黑龙江科技大学 矿业工程学院，黑龙江 哈尔滨150027)

0 引言

煤矿发生的重大事故会对巷道造成不同程度的破坏，甚至引发巷道的垮落，导致救援过程中通道堵塞，此时，快速再造通道尤为重要。目前，我国在垮落巷道方面的研究较少，主要集中在应急救援通道掘进设备上。郝传波等[1-3]阐述了垮塌通道在未来研究中应涉及的有关问题 ，进而针对节理裂隙发育的顶板条件，给出了巷道垮塌类型以及巷道堵塞条件，并提出了相应的工程应用建议；周心权等[4-7]分析了在煤矿爆炸、火灾等重大事故的致灾特征及救灾难度，讨论了煤矿事故防治应用基础研究中应注意的问题；刘晓宇等[8]通过有限元的手段，对巷道的掘进过程进行了模拟，对巷道的应力、应变进行了分析，得出了合理的开挖方式；辛亚军等[9]通过应力转移的思想，提出了巷道再造承载机理，并进行了数值模拟，得出了1种较好的支护手段；李英明等[10-11]通过现场的调研，分析了煤巷的稳定性，并在不同的尺度层面上，分析出2个不同的特征；刘腾飞、汪芸、李学来等[12-14]则是通过利用快速钻孔的技术，借鉴煤矿井下施工大直径钻孔的经验，以尽快实施应急救援、输送救援物资来维持受灾人员生命安全。

综上，现有研究主要集中于巷道垮落形成垮落体的分布形式以及形态，以及如何进行开挖救援，对救援时所需通道的分析较少。矩形通道有在安全救援方面具有方便搭建、成型快、能够快速的形成一条简易通道的优点。由于通道垮落形成的垮落体非常复杂，煤体比较容易破碎，在破坏后形成的散粒体相对简单些，可以按照先易后难的原则，做简化运算，在理想状态下，把块状堆积体视为均质的煤岩散粒体介质(简称为散粒体)。本文以矩形通道为例，通过理论分析以及数值模拟的手段，对再造矩形通道进行受力分析，并将2种方法进行对比，得出矩形通道在散粒体中的应力分布状态。

1 再生救援通道的受力理论分析

1.1 再生救援通道布置方式

由于整个原巷道在动力灾害作用下发生了垮落，顶板上覆岩层和两帮也随之垮落。灾害发生后，煤层通道周围一定范围内的煤体发生垮塌破坏，形成破坏的碎煤。在此范围外的岩体或者煤体没有发生破坏。本文要在破坏范围内，以未破坏底为底板开拓救援通道。垮落体中成通布置模拟如图1所示。 通道所受的应力主要来自区域1、区域2这2个影响区，通道的顶板应力影响区和通道的侧向应力影响区，区域3为原岩影响区。对此进行受力分析，得出垮落体中矩形通道的应力状态。

图1 垮落通道中的成通模拟布置Fig.1 Into a lane simulation of caving roadway layout

1.2 侧壁受力分析

当救援通道重新开挖支护起来后，侧壁受到散粒体的侧向压力，散粒体与侧壁之间的摩擦对确定压应力的在上层散粒介质和下层散粒介质的互力作用下，下部的离散体将要下沉。根据散体力学相关理论[15]分析，矩形通道侧壁和底扳上的压应力与侧壁的粗糙度有关。散粒体与侧壁之间的摩擦对确定压应力的大小及分布起决定性作用。散粒体作用在侧壁的作用力包括受自重影响方向向下的地应力，从而散粒体与通道壁的整体摩擦力方向向上。散粒体相互之间的摩擦力受自身破碎膨胀系数的作用大致是垂直于通道侧壁。通道的侧壁的压力分析分布如图2(a)所示。

图2 通道受力分布Fig.2 Roadway stress analysis

摩擦力大小为σbf1(σb为散粒体对侧壁的压应力；f1为散粒体均侧壁的摩擦系数)，作用在散粒体上，方向向上。取散粒体层高度dh的1层煤介质为单元体，分析其上垂直压力的微分方程为：

Aρgdh+σcpA=(σcp+dσcp)A+σbf1Ldh

(1)

式中：σcp为面积A上的平均垂直压应力，MPa；h为垮落均质散粒体高度，m；L为截面周长，m；A为通道一侧的散粒体面积，m2。

根据通道的具体规格以及围岩参数，f1Ln′/A为定值。令a=f1Ln′/A以简化方程。图2(a)再生救援通道的侧壁受力为：

(2)

式中：n′为侧向压力于平均垂直压力的应力比值，无量纲；ρ为散粒体的密度，kg/m3。侧向应力随高度h的增加趋近其极限值时：

(3)

即计算得：

(4)

式中：σbmax为侧壁应力最大值，MPa。比值A/L=R称为水力半径，代入式(4)得：

(5)

由式(5)可得出最大侧应力值。图2(a)给出了相应的应力分布图，由图2可以看出，侧向应力在侧壁底部达到最大。通过式(5)可知，救援通道两帮受力大小与通道一侧的散粒体水力半径呈正相关，但由于截面周长相对于1个救援通道来说是固定的，所以决定最大值因素的是通道一侧的散粒体面积。

1.3 再生救援通道顶板最大压应力

通道顶板的垂直压力与上部的散粒体的高度有直接线性关系。随着高度的逐渐增高，散粒体的下层承受塑性变形，即在通道的顶板中部达到极限应力状态。由于散粒体沿顶板不可能有大的移动，沿通道顶板的切应力很小，只需要分析压应力。图2(b)为垂直压力线图。破碎的散粒体的高度为h，散粒体中心处的垂直压应力为：

(6)

(7)

式中：n为考虑摩擦力影响后的近壁处侧压应力系数；f为散粒体内摩擦系数。

(8)

依据式(6)～(8)即可得σ0。

2 数值模拟

在厚煤层通道受灾害的影响发生破坏后，其上覆煤层和通道两帮便会随之垮落充填整个巷道的空间，破坏了巷道的原有的形状。原巷道的充填都是破碎的煤块，形成粒径不同的散体，力学性质复杂。破坏之后的通道，因其垮落的块状堆积体几乎充满整个通道，造成救援通道堵塞，且延伸距离较长。因此，要在这散粒体中重新构筑1条新的救援通道，需要分析这个新的救援通道的受力状态。

2.1 参数确定

在模拟实验前，在实验室进行相关参数的测试，数值模拟参数如表1所示。破碎煤样取自冲击地压造成煤层通道破坏的某矿现场。

表1 数值模拟参数Table 1 Numerical simulation parameters

根据实验室测试，松散煤体的弹性模量非常小，由于本文只探讨支护通道的受力情况，采用连续模型代替松散模型，松散煤体看做是弹性模量非常微小的连续体。

通过相关的岩土数值模拟软件可进行相关的计算。采用COMSOL数值模拟软件模拟某矿的通道垮落后再生通道的受力情况。设定矩形通道尺寸为宽×高=3.0 m×3.0 m，通道支护体厚度1.0 m，散体介质为破碎煤块。垮落体宽度和高度分别设定为20 m和40 m。

2.2 应力分析

图3为数值模拟计算得到的垮落体模型应力分布。通过图3可知，模型所受到的应力主要集中于通道的位置。上部垮落体的应力分布呈现中间向两边逐渐增大，但增大幅度较小，当位置靠近通道时，应力会有明显的增大。在通道处所受的应力明显高于上部垮落体。由于模拟是按连续体计算的，则在通道两侧顶角处会出现应力集中区。

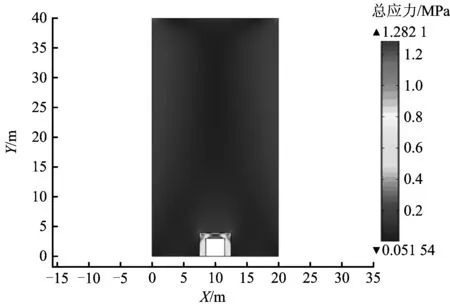
图3 应力云图Fig.3 Displacement cloud

通道顶板应力分布如图4所示，通道侧壁应力分布如图5所示。由图4可知，在通道顶板的两端出现了应力的集中，数值较高，随着位置的变化，逐渐降低。随着顶板位置的变化，应力在1.5 m和3.5 m左右出现了2个波谷，在2.5 m左右出现了1个小型的波峰。由于模型的整体是沿中轴对称的，所以通道侧壁左右两侧应力分布是一致的，由图5(a)和图5(b)所呈现的应力分布也证实了这一点。由于出现了角点的应力集中，由上到下呈应力集中(0 m处)—应力集中消失(1.3 m处)—应力上升(1.3～4.0 m处)，在侧壁底部应力达到最大。

图4 通道顶板应力分布Fig.4 Roadway left side displacement

图5 通道侧壁应力分布Fig.5 The left side of the roadway stress

除去因按连续体计算产生应力集中现象影响外，侧壁的应力分布在底部达到最大，顶板的应力分布在中部达到最大，总体趋势与图5(a)所示的通道侧向应力影响区，以及图4所示的通道顶板应力影响区一致，模拟结果和理论分析基本相符。

2.3 对比分析及展望

通过实验室实验测得散粒体均侧壁的摩擦系数f1为0.2，通过上部顶板的应力计算，得到应力的最大值为4.5×105N/m2，大于数值模拟计算所得的最大值。这种情况的出现，是由于数值计算中上方的散粒体是垂直作用于通道顶板的，未考虑其两侧部分的影响。两侧的部分减弱了顶板上方散粒体对顶板的压应力，从而减弱了中部的最大应力。

将数值模拟中的参数代入式(4)中，利用理论公式计算得到两帮的最大值为3.125×105N/m2，小于数值模拟所得的最大值4×105N/m2，但当上部散粒体同时纳入理论计算中来时，两帮承受应力值为1.171×106N/m2。通过对比上述数据，得到巷道受力示意图，如图6所示。图6中，2区理论计算所得应力值、数值模型模拟计算所得应力值以及2区和3区理论计算所得应力值依次变大，前两者的变化在同一个数量级，而后者应力值明显高于前两者。其中，数值模型模拟计算所得的应力值高于2区理论计算值是由于，3区散粒体重力作用增大了通道两帮所受到的应力，从而使数值模拟的值增大，但上部散粒体并没有使得侧向压应力有质的改变。假设将上部散粒体同时纳入到计算的整体来，使其成为1个大的侧壁时，其计算值大大增加，显然与实际不符。这说明决定巷道侧壁受力的主要因素是其一侧的散粒体，同时上部散粒体会使其增大。

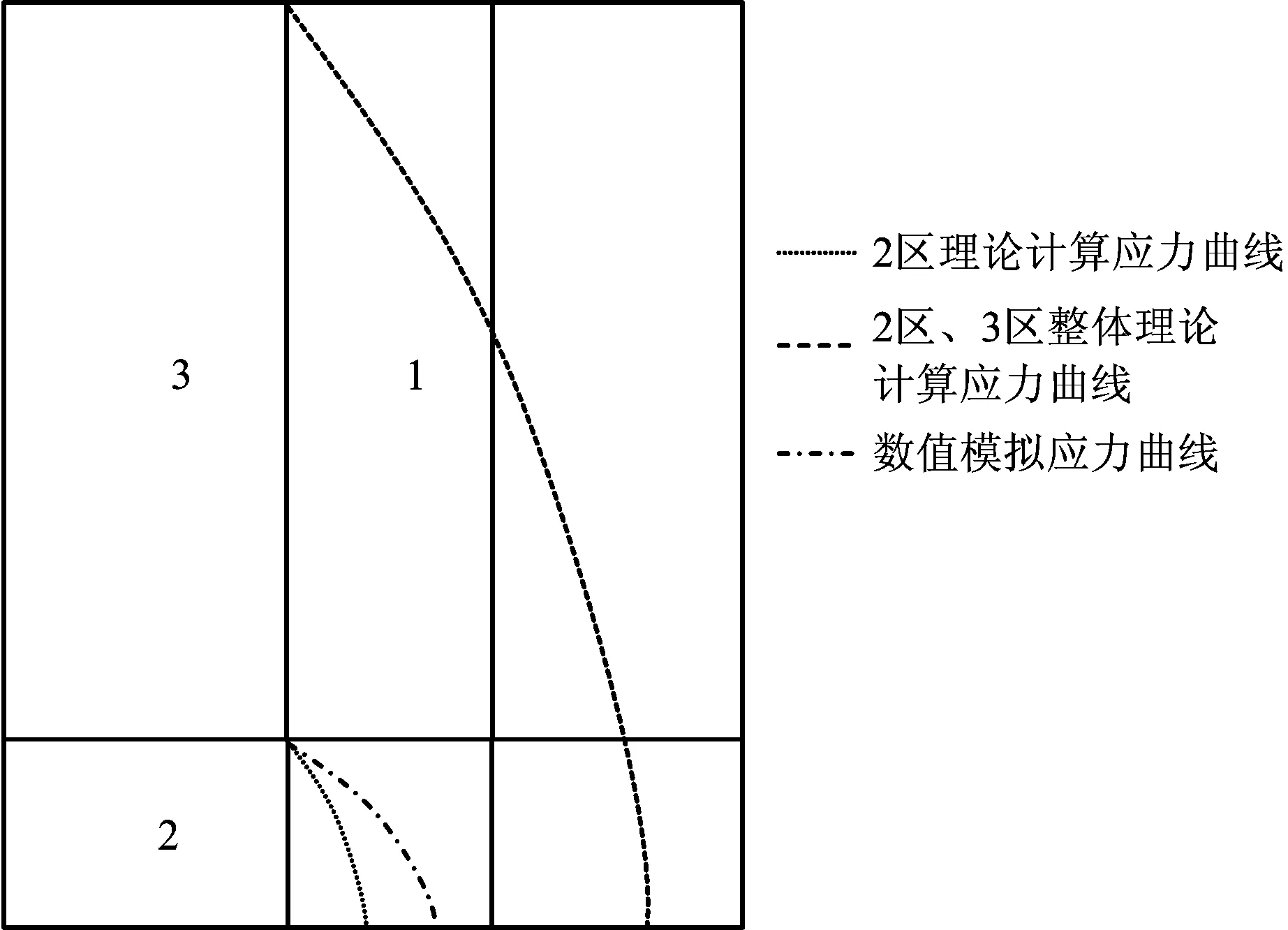
图6 侧壁通道受力示意Fig.6 Schematic diagram of side-wall channel stress

通过对比发现，单独的理论计算结果和数值模拟分析结果有一定的差距。就散体的性质来说，巷道垮落后的构造相当复杂，散粒体的性质受散体颗粒形状和大小、散体中是否含水以及破坏通道原支护体等多种因素影响。本文的参数方法，由于进行了理想散粒体的假设，对通道的影响只是一种宏观的趋势计算。要想完全反映出垮落通道中那些复杂的应力受力状态，并在松散体中形成快速救援的通道，需要将其他因素进一步考虑到散粒体中。可在此基础上做进一步的研究。

3 结论

1)理论分析结果显示，道顶部应力集中区域为中部，通道两帮应力集中区域为根部。

2)数值模拟计算所得的应力结果显示，顶板的应力集中在2.5 m左右位置；两帮的应力集中在4 m左右的位置，与理论分析所得的最大应力位置相一致。

3)在数值方面，顶板理论分析的应力值略大于数值模拟的值，这是由于两侧散粒体的影响，减弱了应力最大值。

4)两帮理论分析值小于数值模拟的最大值，这是由于2区上部散粒体作用，增大了通道两帮所受到的应力。