考虑初始宏细观缺陷的裂隙岩体损伤本构模型研究*

2019-01-05李克钢秦庆词杨宝威张雪娅

中国安全生产科学技术 2018年12期

李克钢，秦庆词，杨宝威，张雪娅，郭文，王庭

(昆明理工大学国土资源工程学院，云南昆明650093)

0 引言

天然地质体中的岩体受地壳运动、人类开挖工程的扰动以及风化侵蚀等作用，岩体内部难以避免地会生成各种不规则原生节理、裂隙网络。节理、裂隙的几何尺寸、物理特性以及空间分布位置的不同，劣化了岩体本身固有的抗压、拉、剪能力，在降低工程岩体稳定性的同时，也给多物理场下的岩体物理力学行为研究带来了极大的困难。随着岩石断裂力学和统计损伤力学理论的不断完善与发展，近年来，已有许多学者基于唯象学角度，运用损伤力学理论对存在初始宏观节理的裂隙岩体损伤本构模型开展了大量且卓有成效的研究，例如：陈蕴生等[1]针对宏观裂隙和微观孔隙2类不同层次损伤的演化特征，确定了表征这2类损伤的奇异损伤变量和分布损伤变量，推导出单向受压条件下非贯通裂隙介质损伤本构方程；赵怡晴等[2]提出考虑宏观和细观缺陷耦合损伤的节理岩体本构模型，证实了初始节理的存在极大地削弱了岩体峰值强度和刚度，而增大了其柔性；袁小青等[3-4]基于Lemaitre 应变等效假设，建立了考虑宏细观缺陷耦合的非贯通裂隙岩体在受载作用下的损伤本构模型；赵航等[5]基于不同加载方式下裂隙岩体中弹性波传播特性，建立了用弹性波波幅来表征的宏细观裂隙耦合损伤的岩体本构模型；曹文贵等[6]从受载条件下岩石孔隙率变化反映体积变化的角度出发，建立了考虑孔隙率变化的裂隙化岩体损伤本构模型；乔彤等[7]引入自然应变，对脆性岩石压密段建立了脆性岩石微裂纹压密段本构模型，压密段存在的本质亦是初始宏细观损伤存在的直观体现。

然而，由于天然地质体节理裂隙的离散性、复杂性以及统计分布函数特征的局限性，以上建立的本构模型在表达岩石全应力应变本构关系中存在1个共性的不足：对于初始含有宏细观缺陷岩石在应力环境中的耦合机制不明确。岩石裂隙的发育程度对岩石各强度特征的响应规律不同，准确定义岩石初始宏细观损伤尤为关键[8-9]。虽然李树春等[10]修正的裂隙岩石初始损伤系数对含有初始损伤的岩石本构有了体现，但其损伤演化机制仍然不够明确。

综上，本文基于weibull分布特征的唯象学观点，运用统计损伤力学对岩石受荷前的宏细观损伤进行定义，优化传统的岩石损伤演化本构模型，通过定义初始损伤，引入初始损伤系数k，建立1种基于初始宏细观缺陷的裂隙岩体损伤本构方程，以期弥补已有本构模型在不同环境下的岩石损伤状态表达的不足，从而揭示初始宏细观缺陷在受力过程中的耦合演变机制，这对多物理场耦合作用研究具有重要意义[11]。

1 考虑初始状态损伤的裂隙岩体损伤本构模型

深埋地下的岩石长期经受多物理场耦合作用影响，使得岩石随机分布着各种微观缺陷，这些微观缺陷以微孔隙、微裂缝及内部微裂纹形式存在。岩石统计损伤力学理论认为，这些随机缺陷服从某种分布，可以通过岩石内部微单元强度变化进行量化，从而研究微缺陷的产生、扩展到损伤累积形成宏观损伤致使岩石失效的过程，其反映的是材料失效的必然性，因此，岩石损伤统计理论得到了较好的发展与应用。

1.1 基于weibull 分布特征的完整岩石受压损伤本构模型

假定岩石材料微单元强度服从weibull 分布[12]，则有：

(1)

式中：m和a均为常数；ε为材料压缩产生的应变。

材料微单元强度服从weibull分布，则可认为材料的损伤D亦服从该分布[12]，则有：

(2)

式中：D为发生破坏的微元占总体微元的比例。

将式(2)带入式(1)，求解得：

(3)

根据岩石损伤力学可知，岩石受压损伤时，引入损伤变量D后的全应力-应变关系式为：

σ=Eε(1-D)

(4)

式中：σ为名义应力，MPa ；E为岩石材料弹性模量，MPa。

将式(3)带入式(4)，有：

(5)

材料常数a，m计算公式如下[12]：

(6)

(7)

则可得完整岩石受荷过程损伤本构关系：

(8)

式(8)中m与式(1)中材料常数意义等同，从物理学意义上，m值越大，反映出材料越接近弹性或脆性状态，反之则越接近于塑性状态；从统计学角度，m值越大，反映出材料越均匀，反之则越离散。因此，可利用形状参数m反映岩石材料的塑性特征。

1.2 考虑初始状态损伤的裂隙岩体损伤本构模型

1.2.1 岩体初始损伤变量的定义

对于完整岩石定义初始损伤变量D=0，即岩石内部不存在宏细观缺陷。事实上室内试验中取芯机所取岩样在试验前均存在宏细观缺陷，裂隙岩体更是如此。为此本文在定义初始状态含宏细观缺陷损伤变量中作出以下假设：

1)试验过程中不存在宏细观缺陷的岩石材料始终为线弹性材料。

2)对于宏细观缺陷的区别以肉眼可见和不可见为基准；研究表明：宏观裂隙的存在导致岩体力学特性显现出明显的各向异性，细观缺陷则显现出各向同性特征[13-15]，初始宏细观损伤对岩石的力学响应特性不同，因此有必要展开初始存在宏细观缺陷对岩石的响应机制研究。

3)将岩石试样试验前存在的损伤状态定义为静态损伤，静态损伤岩石材料即表征含有宏细观缺陷的岩石，采用D1表示试验前含有初始宏观缺陷岩石损伤，D2表示试验前含有初始细观缺陷岩石损伤；将由应力环境改变引起的新附加损伤定义为动态损伤，动态损伤为因受力状态、加载方式以及加载方向等外部条件变化引起的损伤。采用D3表征岩石在受荷载过程中产生的附加损伤，即动态损伤。

4)含有缺陷的岩石在受荷过程中损伤不断累积，直至发展成宏观损伤破坏。从集合的角度，如图1所示，D1表示为试验前岩石试样中宏观缺陷的集合，D2表示为试验前岩石试样中细观缺陷的集合，受力过程中D3均与受力前存在的初始宏细观缺陷发生贯通交互作用，用全集Ω表示无损岩石材料，则受荷载过程中宏细观耦合损伤之间的关系可用集合D123表示为：

D123=D1∪D2∪D3-[(D1∩D3)∪(D2∩D3)]

(9)

图1 裂隙岩体受荷损伤机制示意Fig.1 Schematic diagram of the damage and damage mechanism of fractured rock mass

由图1中的集合关系可知，试验前岩石的损伤程度(即初始存在的宏细观损伤)可用损伤变量D12表示：

D12=D1+D2

(10)

试验过程中受荷载时，D3与试验前存在的初始损伤发生耦合关系，根据损伤原理和Lemaitre应变等效假设可知，试验前含有损伤的岩石弹性模量可等效为：

E12=E(1-D12)

(11)

受力过程中岩石的损伤是渐进连续的，则连续耦合损伤岩石材料的弹性模量为：

E123=E12(1-D3)

(12)

将式(10)、(11)带入式(12)可得：

E123=E(1-D1-D2-D3+D2D3+D1D3)

(13)

式中：E123为裂隙岩石弹性模量，MPa；E为完整岩石弹性模量，MPa。

则岩石在受力过程中初始宏细观缺陷耦合损伤变量D123：

D123=D1+D2+D3-(D1+D2)D3

(14)

试验前，当岩石只含初始宏观缺陷损伤而无细观缺陷损伤时(D2=0)，岩石耦合损伤D123=D1；当荷载环境变化产生动态损伤D3耦合作用时，D123=D1+D3-D1D3。同理，当只有初始细观缺陷损伤而无宏观缺陷损伤时(D1=0)，在受力环境下D123=D2+D3-D2D3，与实际情况吻合。并能够解释刘红岩等[16-17]认为文献[5]提出的宏细观耦合损伤变量D23=D2+D3-D2D3缺乏理论基础的原因，在于其将宏细观损伤简化为宏观可视损伤，即文献[5]的定义方式为本文中单纯考虑存在初始宏观缺陷时在受压试验过程中的耦合损伤，文献[13-15]已述细观损伤对岩石的影响与宏观不同，因此本文定义的损伤变量是合理的，且更全面、具体，物理意义更加明确。

1.2.2 含初始缺陷损伤岩石本构模型

当不考虑初始细观损伤影响时，式(14)表征的是考虑初始宏观损伤影响的耦合损伤变量；当不考虑初始宏观损伤影响时，其表征的是考虑初始细观损伤影响的耦合损伤变量。而对于宏观裂隙，其影响为各向异性，需将其进行张量化(即将损伤变量标量化)，张量化后D1=Disin2β[2]。对于细观损伤D2的确定，由于其产生的影响为各向同性，则张量化后结果相同，即D2=D2。因肉眼难以看见，不便于测量和量化，目前则更多依赖于无损检测仪器(如核磁共振弛豫测量、CT等)以及实验数据的拟合求解。初始损伤系数表征岩石试验前岩石的完整程度，则：

k=1-(D1+D2)

(15)

式中：k为初始损伤系数；D1，D2均为张量化后结果。

将式(15)带入式(14)，可得到试验过程中考虑初始状态宏细观损伤缺陷的耦合连续损伤D123：

D123=1-k+kD3

(16)

式中：D3为由受力引起的岩石内部发生破坏微元与岩石总体微元的比例。

由于微元破坏发生的随机性，假设岩石微元强度服从weibull随机分布，则D3可等效为完整岩石受力发生破坏的微元占总体微元的比例，即：

(17)

结合式(4)和式(16)，同理可得出对试验前含有初始宏细观缺陷损伤的岩石受压过程应力应变本构关系：

σ=E123·ε·(1-D123)

(18)

式中：σ为名义应力，MPa；E123为裂隙岩石材料弹性模量，MPa；D123为试验时受力过程中岩石内部破坏微元占总体微元的比例。

将式(16)、(17)带入式(18)可得裂隙岩石受荷载过程中全应力应变本构方程：

(19)

设微单元破坏前服从广义虎克定律，即可将考虑初始状态损伤全应力应变损伤本构方程推广至三维：

(20)

式中：E为岩石单轴压缩弹性模量，MPa；k为初始损伤系数；μ为岩石泊松比；σ2，σ3为围压，MPa其他符号意义同上。

该方程表征了复杂应力条件下，基于唯象学观点建立的服从weibull分布特征裂隙岩体全应力应变损伤本构关系，m表征裂隙岩石材料微元强度的离散性或宏观塑性强弱特征。

2 初始宏细观缺陷损伤演化特征

2.1 基于weibull分布特征的宏细观损伤参数演化特征

上述确定了含初始宏细观缺陷岩石受荷过程损伤与力学的关系，式中初始损伤系数k和微元强度分布参数m反映了受力作用时岩石的力学特征以及损伤状态。由式(16)可知耦合损伤与静态损伤、动态损伤的耦合关系，如图2所示。

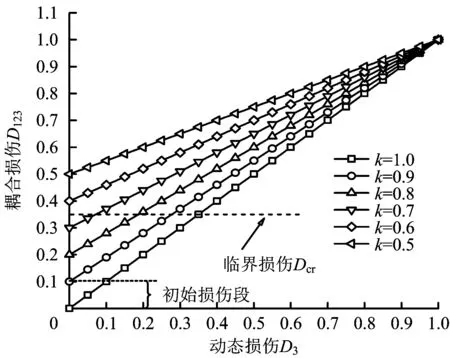
图2 静态损伤与动态损伤耦合关系Fig.2 Static damage and dynamic damage coupling curve

由图2可知，岩石所能承受的临界损伤Dcr是一定的，在受力过程中，动态损伤D3以同等速率增加，则初始损伤越大，其达到临界损伤所需时间越短，即所需破坏时间越短，这与实际是吻合的。假设耦合损伤达到某一定值，将式(15)带入式(16)可得初始损伤在此过程中的演化过程，演化曲线如图3所示。

或

(21)

同理：

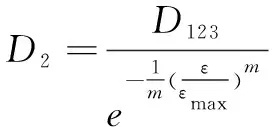
(22)

(23)

图3 受荷过程损伤演化Fig.3 Damage evolution curve of the loaded process

图3显示出宏细观损伤在受荷过程中的演变过程，岩石在受荷过程中经历了4个损伤演化阶段：

1)初始的“无损”阶段。并不是真正“无损”，而是由于孔隙、微裂隙的压密过程并未产生或很少产生新附加损伤。

（2）虽然当前世界局势以和平为基调，各个西方大国的社会形势相对稳定，但是石油储量最为丰富的非洲一些国家近年来国内政局并不稳定，领导人经常更替，不利于胜利油田海外业务的发展。

2)弹性损伤阶段。该阶段宏细观损伤稳定扩展，且扩展缓慢，意味着弹性变形对岩石的损伤影响较小，其损伤主要来自于微元强度较弱的基元。

3)塑性损伤阶段。岩石受压发生塑性损伤，塑性变形使得损伤面积快速增长，显现为损伤加速扩展。

4)峰后损伤破坏阶段。峰后岩石主要发生塑性变形，岩石损伤表现为迅速扩展，岩石完整性随之迅速下降，最终导致岩石破坏。

此演化过程与杨永杰等[18]的物理试验结果吻合。

2.2 weibull分布参数m力学响应分析

前文已经叙述了weibull分布参数m变化带来的响应变化，分布参数m是表征微元强度离散性大小的综合指标，也是宏观强度差异存在的直观表征。因此，分析分布参数m在本文本构方程中带来的力学响应及其损伤演变过程，可揭示岩石受荷损伤过程宏细观缺陷耦合损伤机制。

根据岩石损伤的定义，当岩石达到峰值强度时的损伤为临界损伤Dcr，因此，具有初始宏细观损伤的缺陷的岩石峰值强度σp：

或

(24)

σp=Eεmax(1-Dcr)

由式(24)知，岩石的初始损伤系数与其峰值强度呈线性递增关系，与岩石微元强度分布参数m成负指数关系，从连续损伤的角度，同种性质的岩石初始损伤越大，岩石破坏所需强度越低。则可将初始损伤系数k作为裂隙岩石相比于完整岩石的强度折减系数，1-k则表示损伤场-应力场耦合影响因子，初始损伤系数可通过物理试验确定:

(25)

式中：E为岩石弹性模量，MPa；EM为过峰荷点的割线模量，MPa；σp为峰值强度点，MPa；εmax为峰值应变。

3 模型验证与分析

3.1 本构模型验证

为验证文中所建立的三轴受压损伤演化本构关系的准确性，引用文献[19]的试验数据，分别对砂岩围压为0，3.45，6.90，13.80 MPa时的三轴压缩试验数据进行验证，依据本文公式计算出对应不同围压下的物理力学参数，见表1，由三轴试验结果拟合得到围压与峰值强度和分布参数m的关系如图4所示。

表1 岩石物理力学参数Table 1 Rock physical and mechanical parameters table

图4 峰值应变/分布参数m与围压关系Fig.4 Relationship between peak strain/distribution parameter m and confining pressure

根据图4中拟合结果，得到峰值应变、分布参数与围压关系：

εmax=2.784+0.082 15σ3

(26)

m=3.53-0.064 8σ3

(27)

由此可认为，对于围压对弹模影响较小的红砂岩，在不同围压作用下的峰值应变满足线性递增规律，分布参数满足线性递减规律，该线性关系为：

y=a+bσ3

(28)

式中：a，b分别为拟合参数，可由试验数据拟合求得。

则根据本文模型，红砂岩三轴压缩本构关系为：

(29)

式(29)中假设围压对弹性模量没有影响(如本文所引用数据)，则弹性模量即为单轴压缩下的弹性模量，可根据单轴压缩试验获取三轴压缩试验结果。模型拟合结果如图5所示。

图5 本文模型与实测曲线对比Fig.5 Comparison between the curve of this paper and the measured curve

由图5可知，本文本构模型对不同围压下的红砂岩全应力-应变过程拟合精度较高，说明其合理性与准确性，表明模型是可靠的。

3.2 含初始宏细观损伤岩石不同围压损伤演化特征

以往大量的研究中并未考虑初始宏细观损伤的影响，根据本文建立的损伤演化模型，得出含初始宏细观耦合损伤的三轴压缩损伤演化曲线如图6所示。

图6 红砂岩三轴压缩损伤演化过程Fig.6 Evolution process of triaxial compression damage of red sandstone

由图6可以看出：岩石三轴压缩损伤演化过程经历“无损”→损伤稳定发展→损伤加速累积→损伤迅速累积破坏4个过程。且不同围压下的损伤扩展速率不同，即随着围压的增大，损伤扩展速率放缓，这是由于围压作用岩石塑性软化作用加强，变形承载能力增加。因此，围压的作用可有效延长岩石破坏的时间，增大岩石承载能力，这也揭示了岩石的岩爆发生机制，即卸除围压损伤累积速率加快，导致岩石破坏具有突发性的特点。