基于K-means算法的优秀班集体评选方法

曾 新，杨 健，张 鑫，陶安玲

（大理大学数学与计算机学院，云南大理 671003）

Steinhaus（1955年）、Lloyd（1957年）、Ball&Hall（1965年）和McQueen（1967年）分别从不同的学科研究领域提出了K-means聚类算法，同时，McQueen总结了 Cox〔1〕、Fisher〔2〕、Sebestyen〔3〕等的研究成果，给出了K-means算法的执行步骤，并利用数学方法进行了理论论证。

聚类是一个将整体的数据对象划分为以类或簇存在的包含局部数据对象的过程〔4〕。聚类的目标是使得同一个簇中的对象之间具有较高的相似度，而不同簇中的对象相似度尽可能低。聚类分析是数据挖掘领域重要的研究内容之一〔5-6〕，到目前为止，专家学者基于不同的思想提出了多种聚类算法，大致可以归纳为以下几类〔7〕：基于划分的算法、基于网格的方法、基于密度的方法、基于模型的方法和高维数据的方法，并广泛应用于机器学习、人工智能、图像处理和模式识别等热点研究领域。

由于聚类中心点的选取、簇的个数K和异常点等因素对聚类结果的影响较大，Kaufman等〔8〕提出利用数据点的局部密度计算出K-means聚类算法的K个初始聚类中心，减小随机聚类中心对聚类结果的影响；针对K-means聚类算法是以确定的类数K为前提对数据集进行聚类，而通常聚类数未知的问题，周世兵等〔9-10〕提出最佳聚类数的确定方法；Wang等〔11〕采用神经网络算法进行K-means聚类算法初始聚类中心的选择，得到了较好的聚类效果；谢娟英等〔12〕采用全局方差计算样本的领域密度，选择方差小且相距一定距离的样本作为初始中心点；蔡宇浩等〔13〕针对初始簇中心的随机性问题，提出加权局部方差度量样本的密度，以便更好地发现密度高的样本，并利用改进的最大最小法，启发式地选择簇初始中心点；为了提高传统K-means聚类算法的准确性，王宏杰等〔14〕提出一种结合初始中心优化和特征加权的改进K-means聚类算法；针对传统K-means算法需要人为指定簇的个数和对初始中心点的选取比较敏感等不足，万静等〔15〕提出基于可变网格优化的K-means聚类算法，通过可变网格划分解决了初始中心点不具代表性的问题并排除了噪声干扰问题。

1 K-means聚类算法

1.1 K-means聚类算法的收敛函数K-means聚类算法是一种基于划分的聚类算法，具有思路简洁、收敛速度快等特点，该算法能够将一个含有n个数据点的数据集划分为K个类簇，使得同一簇内的数据点相似度高，而簇间的数据点相似度低。

K-means聚类算法的收敛函数〔16〕如下：

对于给定的一个包含n个d维数据点的数据集X={x1,x2,…,xi,…,xn}，其中xi∈Rd，K表示整个数据集经过K-means聚类算法被划分为数据子集的数目，K个数据子集表示为C={ }ck,k=1,2,…,K，其中每个划分代表一个类ck，每个类ck有一个类中心μk。采用欧几里得距离作为不同数据点间的相似度和距离判断的标准，计算ck类内各点到聚类中心μk的距离平方和DisSum( )ck，见公式（1）：

将收敛函数DisSum()C展开，见公式（3）：

1.2 K-means聚类算法本文应用K-means聚类算法的基本思想如下：

从包含有n个数据点的数据集中随机选取K( )K=3个数据点作为初始聚类中心点，然后采用欧几里得公式计算出每个数据点到K个聚类中心点的距离，并将数据点归类到离其最近的聚类中心点所在的类当中，当所有的数据点归类完成以后，分别计算出每个类中数据点的均值，将类均值作为新的类中心，并重新进行聚类，如此不断循环，直到前后两次聚类中心点相同，则聚类结束。

通过对算法进行分析可以发现，K-means聚类算法的时间复杂度是O( )nKt，其中n是样本数，K是聚类数，t是迭代次数( )K≤t,t≤n，具有可伸缩性和高效率。对于产生类内紧密、类间疏离的聚类结果，具有较好聚类效果。

2 基于K-means算法的优秀班集体评选方法

2.1 传统评选方法存在的弊端传统的优秀班集体遴选方法是将评价班集体的相关属性值进行简单求和，并取总和较大的前K个班级作为优秀班集体，但是评价一个班级是否优秀的属性很多，例如：党员人数、大学英语四六级考试的过级率、计算机等级考试的过级率、获得文明宿舍的次数、参加各类文体活动获奖情况和社会实践的效果等等。因此，对评价班集体的相关属性值进行简单的求和，可能会导致某些班集体在某一方面的表现很突出而成为优秀班集体，而其他均衡发展的班级可能会丧失成为优秀班集体的机会，同时，受到年级的限制，部分低年级的班级属性值较小或为空，对班级的评价影响较大，例如：大学一、二年级的班级党员人数基本为空，而大学英语四六级考试的过级率和计算机等级考试的过级率也可能低于大学三、四年级的班级等。

例1 大理大学数学与计算机学院评选优秀班集体的主要参考属性有党员人数、大学英语四六级考试过级率、计算机等级考试过级率、文明宿舍得分、科研立项获奖和各类文体活动获奖等，部分年级和班级参评数据见表1。其中，2015jil、2015tx、2015tj、2015sx分别表示2015级计科1班、2015级通信班、2015级统计班、2015级数学班。

表1 班集体参评数据

从表1中可以分析出：①如果按照总分排名进行优秀班集体的评选，那么2015级数学班在文体活动方面成绩更加突出，将获得优秀班集体称号，但是从评选班集体的属性值均衡度来说，2015级通信班和2015级统计班的发展更加全面，因此采用属性值简单求和的方式评选优秀班集体并不利于班集体的整体发展，与培养全面发展人才的理念存在差异；②2015级、2016级和2017级采用了相同的班级评价属性和评价方法，受到年级的限制，2016级和2017级的某些班级属性值较小或为空，对班级评价影响较大。而通过分年级选取均衡发展的班集体作为种子数据点，然后以种子数据点为中心进行聚类，直到类中心不发生改变，这种聚类方式可以有效改善传统评选方式存在的弊端。

2.2 基于K-means算法的优秀班集体评选方法首先将真实数据集按年级进行划分，分别得到2015级、2016级和2017级各班级的参评数据，然后从3个年级的数据集当中分别选取所有属性取值较平均的班级（均衡发展班级）、若干属性取值较大的班级（偏离发展班级）和大多数属性取值较小的班级（最差发展班级）作为初始聚类的中心，按K-means聚类算法的执行过程，将各年级的数据集分别聚为3类，最后将均衡发展的类内的班级作为本年级的优秀班集体。具体的实现过程如下。

2015级各班级的参评数据见表2。其中，2015xx表示2015级信息班。对2015级班集体相关属性取值进行分析，分别选取2015tx、2015sx和2015ji1作为均衡发展、偏离发展和最差发展班级的初始聚类中心点，通过实验得到基于K-means算法的聚类结果见表3，聚类方法与传统方法的优秀班集体结果对比见表4。

表2 2015级各班参评数据

表3 聚类结果

表4 优秀班集体对比

2016级各班级的参评数据见表5。对2016级班集体相关属性取值进行分析，分别选取2016sx、2016xx和2016ji1作为均衡发展、偏离发展和最差发展班级的初始聚类中心点，通过实验得到基于K-means算法的聚类结果见表6，聚类方法与传统方法的优秀班集体结果对比见表7。

表5 2016级各班参评数据

表6 聚类结果

表7 优秀班集体对比

2017级各班级的参评数据见表8。对2017级班集体相关属性取值进行分析，分别选取2017tx、2017xx和2017ji1作为均衡发展、偏离发展和最差发展班级的初始聚类中心点，通过实验得到基于K-means算法的聚类结果见表9，聚类方法与传统方法的优秀班集体结果对比见表10。

表8 2017级各班参评数据

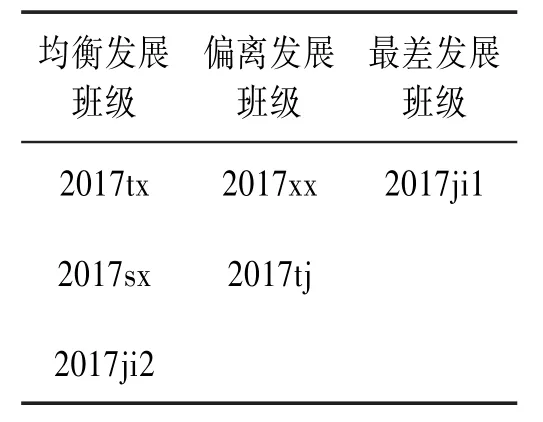
表9 聚类结果

表10 优秀班集体对比

从3个年级分别采用基于K-means算法的评选方法和传统评选方法的结果对比表中可以分析出：基于K-means算法的评选结果与传统评选结果存在部分重叠的情况，是因为部分班级不仅总分高，而且班级各属性值都较均衡，同时可以说明，新的优秀班集体评选方法，在传统评选方法的基础上兼顾了班级各项评价属性的均衡发展。

最后将3个年级的数据进行合并，利用基于K-means算法的评选方法和传统评选方法的结果对比。见表11。

表11 优秀班集体对比

从表11中可以看出：基于K-means算法的评选方法得到的结果都是2015级的班级，这是因为其年级较高，评价班级的相关属性基本都有取值，而传统评选方法得到的结果也基本都是较高年级的班级，同时，其存在部分属性取值较高的、发展失衡的情况。因此，采用基于K-means算法的优秀班集体评选方法，选取不同年级内均衡发展的优秀班集体，比传统评选方法更合理。

3 总结

基于K-means算法的优秀班集体评选方法，在选取均衡发展的班集体作为种子数据点后，将种子数据点作为聚类的初始中心，采用K-means聚类算法进行聚类，直到类中心不发生改变或前后两次收敛函数值之差小于给定阈值，则聚类结束，并将种子数据点所在的类内的所有数据点作为优秀班集体。采用K-means聚类算法“类内紧密、类间疏离”的特点进行优秀班集体的评选，能够将均衡发展的班集体聚在同一类，解决了传统评选方式中班集体因为某一方面表现突出而被评为优秀的弊端。