基于连续Hopfield网络的复杂网络社团结构提取

代婷婷，董延寿，韩 艳

（昭通学院数学与统计学院，云南昭通 657000）

一个是1998年Watts和Strogatz发表在Nature上的文章〔1〕揭示了复杂网络的小世界特性；另一个是1999年Barabási和Albert发表在Science上的文章〔2〕揭示了复杂网络的无标度性质，认为网络的这种性质缘于两个缺一不可的演化要素，并据此提出了一个网络模型，传统的网络模型是建立在随机图基础上的〔3〕。

对于复杂网络的研究主要是研究其社团结构，关于复杂网络中的社团结构提取有很多的算法。Girvan 和 Newman〔4〕在2002年提出了一种通过边移除按层次分解网络的社团结构方法（GN）。此项研究工作被认为是现代社团结构研究的开创性工作，各研究领域的研究员对此有着广泛的兴趣。GN算法寻找最可能处于社团之间的边，通过不断地将这些边移除得到网络的层次划分。Radicchi等〔5〕针对GN算法进行了一些改善，提出了一个新的GN自包含算法。

1 算法

1.1 连续神经网络求解矩阵的特征值及特征向量考虑微分方程

其中，A是一个n×n的实对称矩阵，可以将其视为神经网络的连接权强度，X∈Rn，视为神经网络的状态，那么方程（1）就描述了一类连续型的全反馈人工神经网络。Radicchi等〔5〕给出了一种电路模拟方法，当A为对称正定矩阵时，OJA等〔6〕根据神经网络的Hebbian规则，将方程（1）作为一种无教师指导的神经网络学习过程，研究了输入空间提取特征主元的问题，证明了方程（1）从任意初始值出发的解都收敛于A的最大特征值对应的特征向量。这个可以由下面的定理保证。

定理1假设A的最大特征值λ＞0，则式（1）的从任意初值X(0)Rn出发的解均收敛于A的最大特征值λ对应的特征向量〔7〕。

该定理给出了一种新的求解矩阵特征值和特征向量的方法。

1.2 社团提取问题中的模块度函数假定网络包含有n个节点，对于一个网络进行特殊的划分，即将网络划分为两个组，让si=1表示节点i属于第一组，当si=-1时，表示节点i属于第二组。将节点i和节点j之间边的连接数目表示为Aij（其值取0和1）。若网络中有重边存在，则Aij可以取比1大的值。Aij就是所谓的网络邻接矩阵中的元素，若节点i和节点j之间边的连接是随机的，则均值为kikj/2m，ki表示节点i的度，i=1,2,...,n，m=表示网络中边的总数目，则文献〔7〕中的社团提取问题中模块度函数Q可定义为

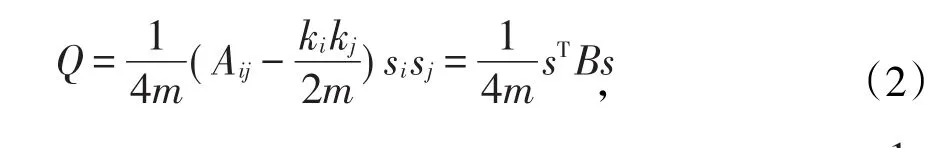
这里s表示向量，其第i个元素为si，i=1,2,...,n是个常数。而对称矩阵B称为模块度矩阵，其元素为：

利用（3）式将矩阵B进行化简发现它的行和与列和都为零，因此矩阵B总有特征向量(1,1,1,...)，其对应的特征值为0，这是拉普拉斯图矩阵的性质〔7〕，也是图分割的基础。

1.3 连续神经网络提取复杂网络社团结构的算法（CNN） Newman〔7〕将模块度函数Q定义为（2）式，模块度矩阵B定义为（3）式，若考虑复杂网络为无向网络，则邻接矩阵A是一个实对称矩阵，从（3）式可知模块度矩阵B也是一个实对称矩阵，所以根据Fortunato等〔8〕的阐述，可以利用方程（1）的神经网络系统求解出模块度矩阵B的最大特征值对应的特征向量，与此同时，结合Newman的特征值特征向量提取社团结构的算法的原理，就可以不用计算模块度矩阵B的最大特征值对应的特征向量，而直接通过解微分方程（1），利用微分方程（1）的解中元素的符号就可以将复杂网络中的节点分为两类。据此，提出了如下CNN算法。

针对复杂网络的社团结构检测问题，将Newman的基于模块度函数Q的矩阵特征值和特征向量提取复杂网络中社团结构的算法和神经网络算法求解矩阵特征值特征向量的算法结合起来得到一种新的基于连续神经网络的社团结构检测算法，简称CNN算法，模型为：

其中，B为（2）式定义的复杂网络的模块度矩阵，X∈Rn，由定理1知，从任意初值出发，方程（3）的解都会收敛到模块度矩阵B的最大特征值对应的特征向量。结合Newman的特征值特征向量算法，就可以根据方程（3）的解中元素的符号将复杂网络中的社团结构提取出来。

综上所述，设复杂网络的邻接矩阵为A，本文给出的基于CNN的社团结构提取算法的步骤如下：

步骤1：计算复杂网络的模块度矩阵B，其中的元素为 ，ki表示节点i的度，ij表示复杂网络的邻接矩阵A的元素；X(0)=BX(t)-

步骤2：给定任意初值 ，求解XT(t)BX(t)的X(解t)X∗；

步骤3：根据解X∗得到社团结构标签向量s，其中向量s中的元素如下确定

步骤4：将s中+1对应的节点提取出来。

2 结果

2.1 实验数据在本文中，采用了空手道俱乐部网络（Zachary's Karate Club Network）〔9〕数据做实验。该网络数据的下载网址是 http：∕www-personal.umich.edu∕～mejn∕netdata∕。

空手道俱乐部网络：在社团提取问题中空手道俱乐部网络是被应用最为广泛的例子之一。空手道俱乐部网络由34个节点组成，每个节点表示一个成员，网络中的78条边表示成员之间的社会交往关系，由于俱乐部主管和校长之间发生矛盾，俱乐部成员就被分成了分别以主管和校长为中心的两个社团。

2.2 实验结果及分析在实验部分，将在俱乐部网络上分析连续神经网络算法的稳定性以及分类效果，分别选出俱乐部网络中所有的节点和某几个节点分析CNN算法的稳定性，结果见图1～2。

图1 CNN算法在空手道俱乐部网络上的稳定性分析

图2 CNN算法下空手道俱乐部网络上某几个点的稳定性分析

从图1可以看出，当t=0时，对于任意的初始值X(0)，随着时间的推移，发现俱乐部网络中的每个节点所对应的网络状态最终收敛到一个稳定状态，即收敛到俱乐部网络的模块度矩阵B的最大特征值对应的特征向量。因此根据网络稳定状态的符号提取出俱乐部网络中的社团结构。从图2可以更清楚地看到CNN网络中的某几个状态的收敛情况，给定任意的初值X(0)后，只需1.5s,网络中的0、2、3、32、33这5个节点的网络演进就达到了稳定状态。这表明CNN算法的稳定性良好。

采用连续神经网络算法提取空手道俱乐部网络中的社团结构，结果见图3。

图3 连续算法提取空手道俱乐部网络中社团结构的分类结果

图3列出了连续神经网络算法在空手道俱乐部网络上的仿真结果。从实验结果发现，特征向量算法、连续算法对空手道俱乐部网络的分类结果与特征向量算法的分类结果（Q=0.3715）相同，表明本文中的算法也是合理的。

3 讨论

复杂网络是研究复杂系统的有力工具，很多现实的系统都可以抽象成复杂网络来研究，网络的节点对应着系统中的实体。研究表明，很多真实网络中存在着不同程度的社团结构特性，而这种社团结构决定着网络的某些功能属性，因此在网络中描述和检测这些社团结构具有重要的实际意义。本文立足于检测复杂网络中的社团结构这个课题，提出了基于模块度函数Q这个指标的社团结构提取算法——连续神经网络算法，并且将该算法和已有的相关算法作了比较，表明了此算法的有效性。