关于Fermat型函数方程的整函数解
2019-01-04段江梅杨惠娟
段江梅,韩 艳,杨惠娟
(昭通学院数学与统计学院,云南昭通 657000)
1 引言及主要结果

在整函数环,或是亚纯函数域上的非平凡解。Hayman〔1〕证明了:
定理A当n≥9时,方程(1)不存在非常数亚纯解。
定理B当n≥7时,方程(1)不存在非常数整函数解。
此外,当2≤n≤5 时,G.G.Gundersen等〔2-3〕找到了满足方程(1)的非常数整函数解;当n=6时,G.G.Gundersen〔4〕构造了满足方程(1)的非常数亚纯解〔5-6〕。
对于n=7,8,是否存在非常数亚纯函数f(zg),(zh),(z)满足方程(1),以及对于n=6是否存在非常数整函数f(zg),(zh),(z)满足方程(1)的问题,目前还没有完全解决。
本文主要研究函数方程

1985年,Hayman研究了Fermat型函数方程
整函数解的存在性问题。对于n≥13,仇惠玲〔7〕证明了:
定理C当n≥13时,方程(2)不存在非常数整函数解。
本文对于n=12,方程(2)整函数解的存在性问题进行探究,得到结论:
定理设f1(z),f2(z),f和3(zf)4(z均)为非常数整函数,它们满足:
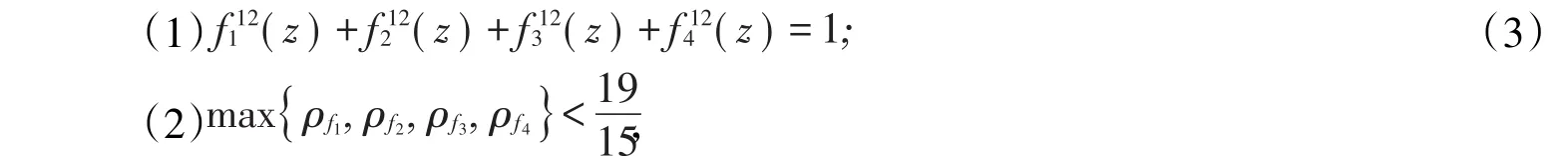
则存在非零常数c,使得
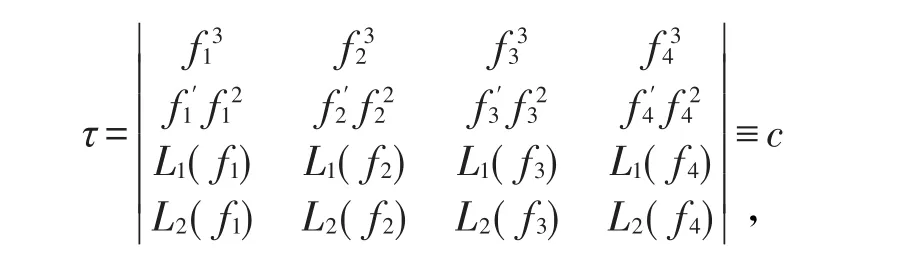
其中L1(fm)
2 几个引理
引理1若f(z)是C上的亚纯函数,那么对∀k∈N,f(k)(z)与f(z)的级相同〔8〕。
引理2若φj(z)(j=1,2,…,k)为区域D内k个亚纯函数,且φ1,φ2,…,φk线性无关,那么φ1,…,φk的Wronskian行列式〔9〕
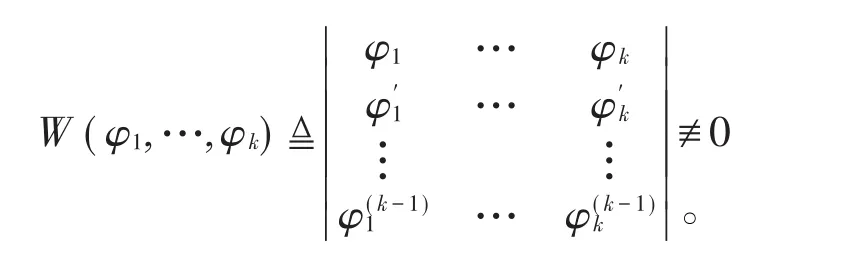
引理3若f(z是)非常数亚纯函数,其级ρf<+∞,那么对于∀ε>0,存在E⊂(1,+∞,)使得E的对数测度有穷(即,且〔10-11〕
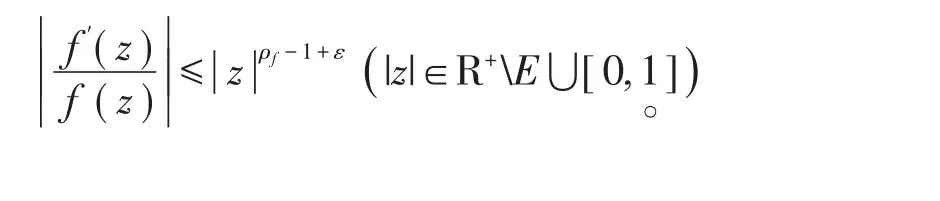
3 定理的证明
由于f1,f2,f3,f4是方程(3)的非常数整函数解,则一定线性无关。事实上,若线性相关,则存在不全为零的常数c1,c2,c3,c4,使得不失一般性,假设c4≠0,结合(3)式得
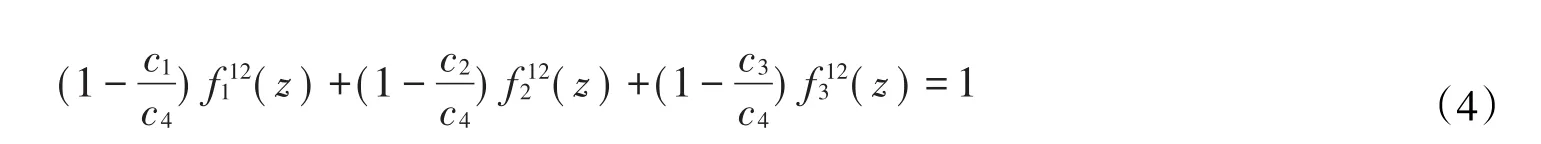
由(3)式可得方程组
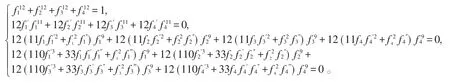
由于
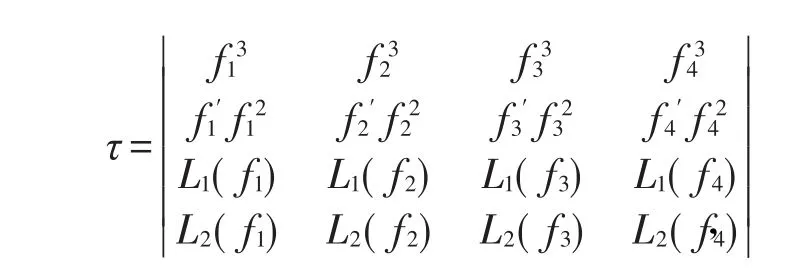
其中L1(fm)=
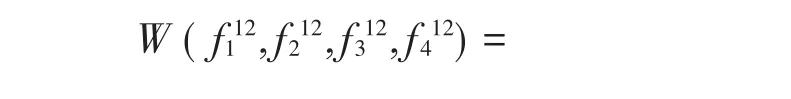
从而

另一方面,由克莱姆法则得
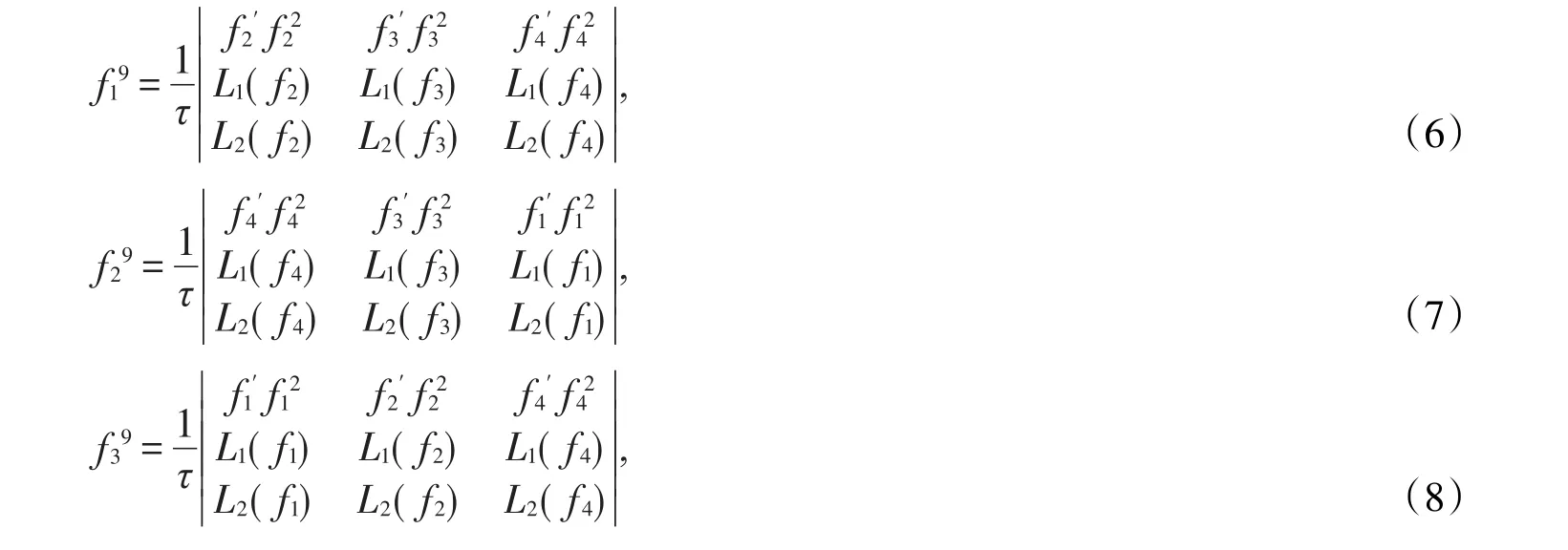
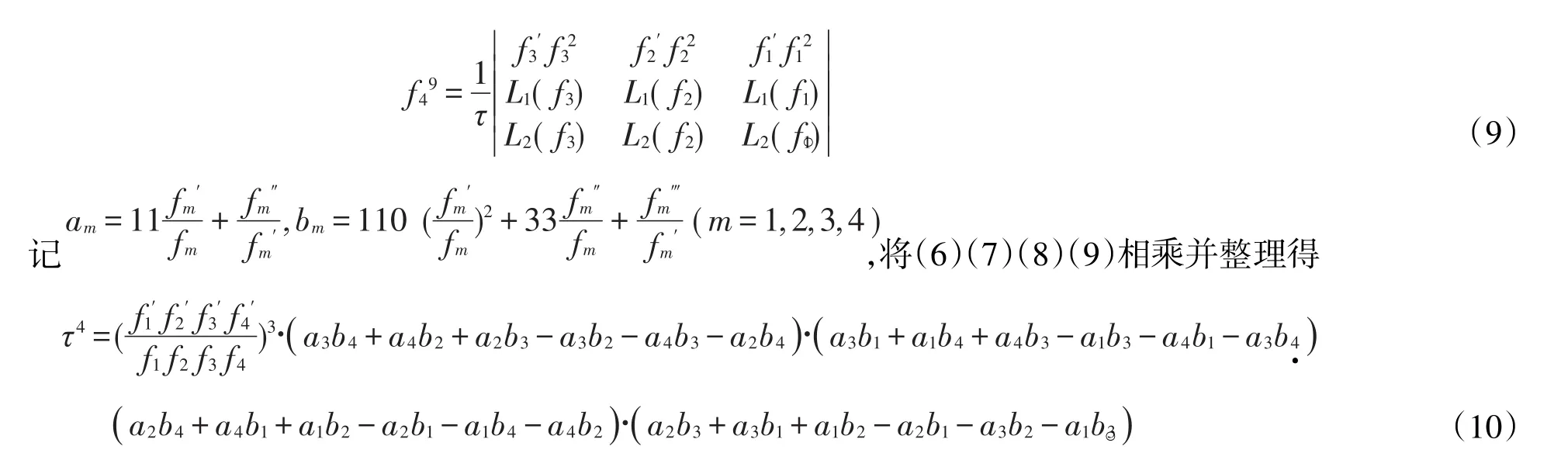
记ρ=max,由引理1知
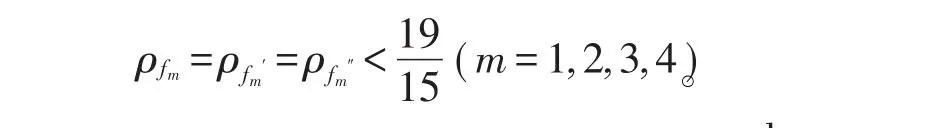
又由(10)式及引理3知,对于∀ε>0,存在E⊂(1,+∞),使得且
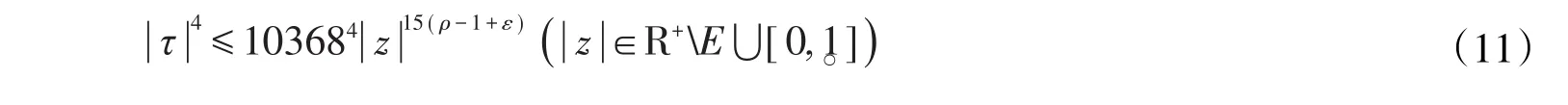
又由(5)式知,必存在非零常数c,使得τ≡c,证毕。
