WSTi3515S阻燃钛合金超塑性变形行为及本构关系研究

张学敏，曹宇霞，李 悦，焦奔奇,梁梦妍,袁战伟,曾卫东

(1.长安大学,陕西 西安 710064)(2.西北工业大学 凝固技术国家重点实验室,陕西 西安 710072)

0 引 言

为了防止发动机中钛合金燃烧事故的发生，减轻飞机重量，满足高推重比先进航空发动机的需要，各国竞相开展了阻燃钛合金的研制工作。2011年，西部超导材料科技股份有限公司联合西北有色金属研究院、北京航空材料研究院、西北工业大学等单位在美国研制的Alloy C(Ti-35V-15Cr)、Alloy C+(Ti-35V-15Cr-0.6Si-0.05C)和我国研制的Ti40(Ti-25V-15Cr-0.2Si) 合金的基础上，通过调整V、Si、C元素含量，成功研制了一种新型高合金化β型阻燃钛合金WSTi3515S合金(Ti-35V-15Cr-xSi-yC)[1]。目前已对该合金的热物理性能、力学性能、热暴露性能、工程化制备等方面进行了深入研究[2-5]，但有关其超塑性成形的研究尚未见报道。这可能是由于WSTi3515S阻燃钛合金内部为单相粗大β晶粒，不能满足细晶超塑性要求晶粒粒径小于10 μm的前提条件。然而，近年研究表明具有粗大晶粒的钛合金在适当的变形条件下也具有良好的超塑性[6-8]。大晶粒超塑性的实现对于缩短工艺流程，提高生产效率具有重要意义。鉴于此，研究了WSTi3515S阻燃钛合金超塑性拉伸的力学行为，建立合金的超塑性本构方程，旨在探讨WSTi3515S阻燃钛合金的最佳超塑性变形条件，描述材料变形时热力学参数之间的关系模型，为后续有限元数值模拟以及制定和优化成形工艺参数提供依据。

1 实 验

实验材料为热轧退火态WSTi3515S合金，其原始组织为粗大的单相β晶粒，晶粒尺寸约为32 μm(图1)。通过线切割将试样加工成标距尺寸为10 mm×6 mm×2 mm的拉伸试样，在试样表面涂覆高温抗氧化涂料。在大气气氛下，采用CMT4104型电子万能实验机进行等温恒应变速率拉伸试验，拉伸方向与轧制方向相同，试验温度范围为800～920 ℃(温度间隔为40 ℃)，应变速率为0.000 5、0.001、0.005、0.01 s-1。

图1 热轧退火态WSTi3515S合金的原始组织Fig.1 Original microstructure of roll-annealing WSTi3515S alloy

2 结果与分析

2.1 断裂延伸率

图2为WSTi3515S阻燃钛合金板材在不同条件下拉伸后的延伸率。从图2可以看出，应变速率较低时(0.000 5～0.001 s-1)，试样的延伸率均达到300%以上，表现出良好的超塑性能，在变形条件为920 ℃、0.000 5 s-1时获得最大延伸率556%。随着应变速率增加，WSTi3515S合金的延伸率显著减小，尤其在低温(800 ℃)下，延伸率仅为186%左右。可见，WSTi3515S合金的大晶粒超塑性行为对于应变速率和温度都非常敏感，但是仍具有相当宽的超塑性温度范围及应变速率区间。

图2 WSTi3515S合金延伸率随温度的变化曲线Fig.2 Curves of elongation various with temperature of WSTi3515S alloy

2.2 真应力-真应变曲线

WSTi3515S 合金超塑性拉伸变形的真应力-真应变曲线如图3所示。从图3可以看出，WSTi3515S合金在单轴拉伸过程中，稳态变形阶段很短甚至不出现，变形主要集中在准稳态变形阶段，且准稳态变形阶段越长，获得的延伸率越大。

准稳态变形区可以分为2个阶段。第1阶段为真应力逐渐升高的应变硬化阶段。屈服之后，试样在变形过程中表现出持续应变硬化行为，这种现象在Ti-6Al-4V合金的超塑性变形中也有发现[9-10]。研究认为，适当的硬化可有效抑制颈缩。硬化速率越慢，流动应力越稳定，越容易获得高的延伸率。结合本研究中WSTi3515S合金的大晶粒特性，认为超塑性变形出现应变硬化的原因主要是由位错塞积引起的。变形过程中只有处于有利取向的晶界才能产生滑移并参与合金变形，其余晶粒特别是大晶粒仍发生晶内滑移。晶内滑移造成位错数量急剧上升，导致位错塞积，引起应力上升。第2阶段为真应力越过峰值后下降的应变软化阶段。超塑变形中产生应变软化的原因主要有2个：①动态再结晶；②几何颈缩。动态再结晶既可细化晶粒，又能引起应力松弛，使晶界滑移过程更容易进行，促使进一步变形所需的应力显著降低。典型的动态再结晶现象已在粗晶Ti40阻燃钛合金超塑性变形中观察到，其真应力-应变曲线与WSTi3515S合金的变化趋势类似[11]。几何颈缩包括内颈缩和宏观颈缩。变形时因内部空洞所占体积的增大和试样变形不均匀性的增加，流变应力的计算值会降低。

图3 WSTi3515S合金在不同应变速率下的真应力-真应变曲线Fig.3 True stress-strain curves of WSTi3515S alloy at different strain rates:(a)0.000 5 s-1；(b)0.001 s-1；(c)0.005 s-1；(d)0.01 s-1

2.3 应变速率敏感指数m值分析

2.4 WSTi3515S阻燃钛合金超塑性变形本构关系

WSTi3515S合金在超塑性变形时受到多种热力参数的影响，可通过建立这些参数与材料流动应力之间的函数关系即本构方程来表征其超塑性行为。

图4 WSTi3515S合金的关系曲线 curves of WSTi3515S alloy

2.4.1 Arrhenius方程

超塑性变形过程属于高温变形范畴，也是一个热激活过程，其变形温度、应变速率对流变应力的影响可用Arrhenius方程表示[12]。

(1)

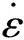
对方程(1)两边分别取自然对数，并设变形激活能Q与温度T无关，整理可得：

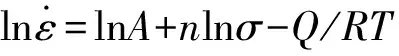
(2)

由方程(2)求偏导可得：

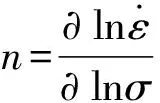
(3)

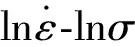
图5 WSTi3515S 合金的关系曲线 curves of WSTi3515S alloy

由方程(2)可导出变形激活能的表达式为：

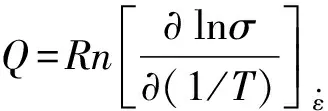
(4)

Q=Rnk

(5)

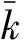
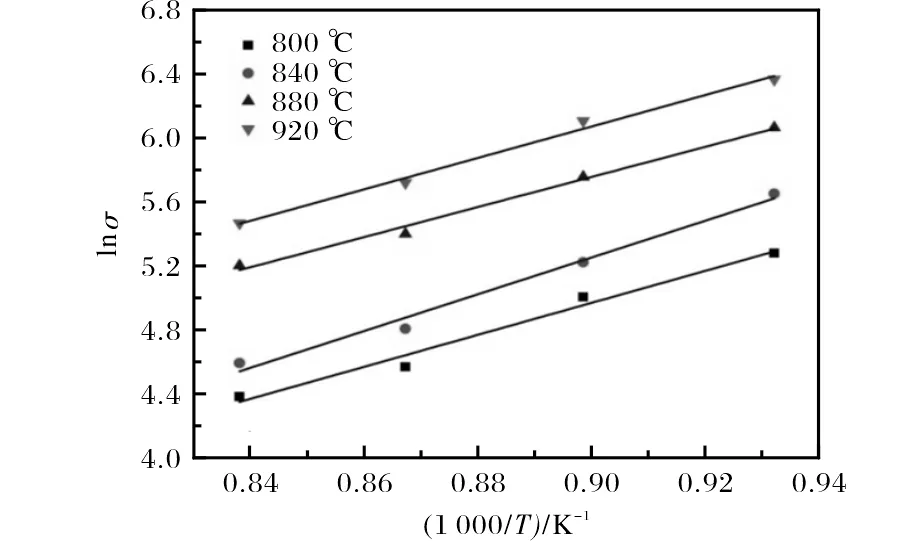
图6 WSTi3515S合金的lnσ-1/T关系曲线Fig.6 lnσ-1/T curves of WSTi3515S alloy

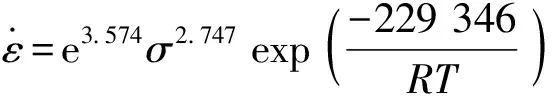
(6)

(7)

为了验证所建立的本构方程的精确度，对不同温度下的流动应力计算值与实验值进行比较，结果如图7所示。从图7可以看出，所有数据点的相对误差均小于15%，但部分数据点的相对误差超过了10%，所构建的本构方程的精度并不高，因此需要通过更好的方式建立精度更高的本构模型。

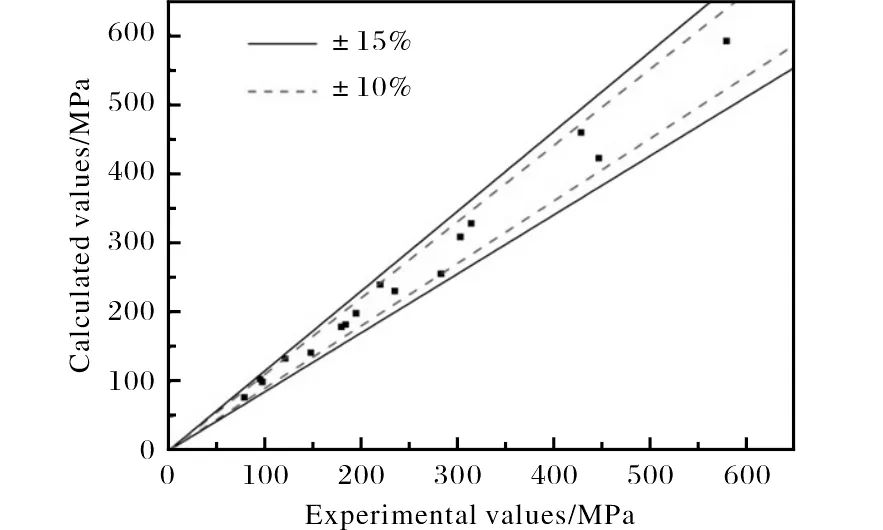
图7 Arrhenius本构方程误差精度效果图Fig.7 Diagram of error precision of Arrhenius constitutive equation

2.4.2 多项式模型

多项式模型由于其计算精度高、拟合系数数量级相近等特点，已被广泛应用于经济、医学、交通、工业控制等领域。常见的多项式模型包括温度幂指数模型[13-14]、逐步回归模型[15-16]和正交多项式模型[17]。本研究在逐步回归模型基础上，充分考虑应变、应变速率和温度对流动应力的综合影响，提出如下本构模型:

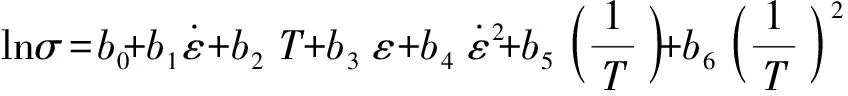
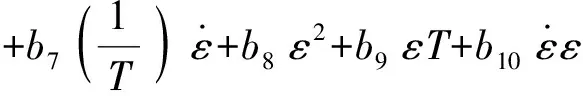
(8)

利用SPSS软件对实验数据进行多元线性回归所获得的回归系数:b0=-8.046，b1=186，b2=0.006，b3=0，b4=-10 805.508，b5=0，b6=10 065 622.27，b7=27 872.619，b8=0.946，b9=-1 184.197，b10=35.738。

对多项式模型本构方程计算的流动应力值与实验值进行比较，结果如图8所示。由图8可以看出，计数值与实验值吻合程度较好，所有数据点的相对误差均小于10%，相对误差小于5%的数据点占总数据点的81.25%。因此，所构建本构方程的精度较高，能够满足数值模拟的精度要求。

图8 多项式模型本构方程误差精度效果图Fig.8 Diagram of error precision of polynomial model constitutive equation

3 结 论

(1) 原始晶粒粗大的WSTi3515S合金可在较宽的温度范围及应变速率区间内实现超塑性。合金在高温低应变速率条件下具有良好的超塑性能，延伸率均在300%以上。最佳超塑性变形条件为920 ℃、0.000 5 s-1，该条件下获得的最大延伸率为556%。

(2) WSTi3515S合金在超塑性拉伸过程中，稳态变形阶段很短甚至不出现，变形主要集中在准稳态变形阶段，且准稳态变形阶段越长，获得的延伸率越大。

(3) 采用Arrhenuis型方程建立的WSTi3515S合金超塑性本构关系精度不高；采用多项式模型构建的本构方程，相对误差基本在5%以内，能够满足数值模拟的精度要求。