基于柔性控制点的三维数据拼接方法

兰志广，张洋，张致远，李汝鹏，刘巍，邢宏文

(1.大连理工大学 机械工程学院，辽宁 大连 116024；2.国家商用飞机制造工程研究中心，上海 200127)

0 引言

在航空航天等领域，为保证零件的加工精度及部件的装配精度，需要对零件的三维几何尺寸等数据进行精确的测量。目前，机器视觉测量凭借其测量精度高、速度快、非接触及易于操作等优点，已被广泛应用于工业现场[1-2]。然而，航空航天的零部件外形尺寸一般较大，且放置于型架上，在特定的方向上存在遮挡等现象，仅凭传感器的单一测量视场无法实现整个零部件的高精度全局测量要求[3-4]。因此需要利用多视数据拼接技术，即将多视场传感器获得的局部测量数据通过拼接算法融合在同一个坐标系下，从而获得大型零部件完整的外形三维数据。

目前，三维数据全局拼接方法可根据数据的获取流程分为三类：一类是机械运动式拼接法[5]，即利用机械结构获取各次测量传感器绝对位置，从而将局部数据根据绝对位置转换至同一坐标系下，完成测量数据的拼接。该类方法具有操作方便的优点，但是其拼接精度取决于运动机构的精度[6]，运动机构的尺寸范围一般较小，主要适用于中小零部件的拼接测量。第二类是公共区域顺序拼接法[7-8]，即在相邻的两个测量视场的公共区域内布置特征信息，通过特征信息在两个不同传感器的坐标值利用坐标转换算法来求得这两个传感器的转换关系，从而将后一传感器获得的坐标值转换至前一传感器坐标系下，以此类推，将其他所有传感器获得的坐标转换至第一个传感器坐标系下，最后完成数据拼接。如北航刘震等人，利用同心圆靶标作为特征信息，放置在相邻两个测量视场的公共区域，实现三维数据的拼接[8]。此类方法针对较小零件测量时，由于坐标转换次数较少，需要设备较少，且操作简便，具有很大的优势。然而在测量较大的零部件时，如长达10多米的机翼等，由于数据拼接的次数多会产生严重的累积误差[9]，拼接精度较低。且在相邻的两个测量区域的公共视场内要有足够多的特征信息，对特征信息的布置和测量传感器的拍摄角度都有较高的要求。第三类是全局控制拼接法[10-15]，即利用全局控制装置测量传感器在每一位置的位姿，获得各个位置局部传感器坐标系到全局坐标系的转换关系，从而将所有局部信息统一至全局坐标系下，完成拼接。如R.S.Lu等人利用双经纬仪系统作为全局控制装置，视觉传感器作为局部测量系统，视觉传感器测量被测物获得三维数据，双经纬仪测量视觉传感器的位置求得局部测量坐标系到全局坐标系的转换关系，将局部数据转换至全局坐标系下，实现拼接测量[16]。该类方法的转换链简单，具有很高的拼接精度，广泛应用于大型零部件的三维测量中[17-18]。然而，利用现有方法需要提前对全局控制点进行布局并手工粘贴，效率低，例如对于3×3 m的零件粘贴控制点大概需要1小时左右，另外还需要时间手动揭下控制点;且飞机机翼蒙皮、天线罩等对表面质量要求很高的精密零件，表面不允许粘贴控制点，因此粘贴控制点的全局拼接方法适用范围有限。

针对具有自由曲面的大型零件的快速全局测量，本文利用双目视觉，提出了一种基于柔性投影全局控制点的全局三维数据拼接方法。该方法不需要预先布置控制点，省去了繁琐的布点流程，可根据零件表面特征自由安排测量站位，现场适应性高，并且由于坐标转换简便，不会随着局部测量次数的增多而产生累积误差，具有非常高的拼接精度。

1 全局三维数据拼接方法

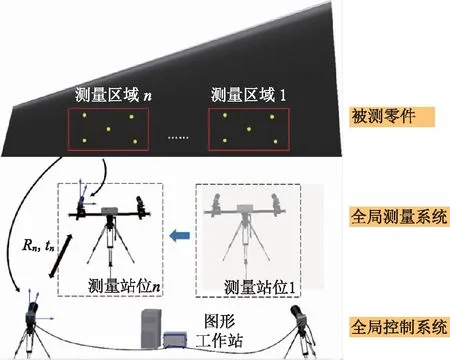
图1 基于柔性控制点的全局三维数据拼接原理图

基于柔性控制点的全局三维数据拼接原理如图1所示。全局测量系统由前后两套双目视觉测量系统和一台投影仪组成。其中，后面的双目视觉测量系统采用两台分辨力高且视场大的工业相机作为全局控制系统，固定于测量区域后方，用于建立全局坐标系；采用两台视场较小的工业相机作为局部测量系统，放置于测量区域的前方，可随时移动用以获取被测零件不同区域的局部信息；投影仪用以投影柔性控制点阵，投影出的点阵可同时被两套双目系统采集到，以实现局部坐标系到全局坐标系的坐标转换。利用全局控制系统和局部测量系统分别对柔性控制点进行采集，获得局部坐标系与全局坐标系间的转换矩阵，从而实现不同位置三维点云数据的拼接。

1.1 全局坐标系与局部坐标系的建立

为实现大型零件三维点云数据的拼接，首先应建立全局控制坐标系(后文简称全局坐标系)和局部测量坐标系(后文简称局部坐标系)，本文将全局坐标系建立在全局控制系统中左相机的相机坐标系上，如图2所示。

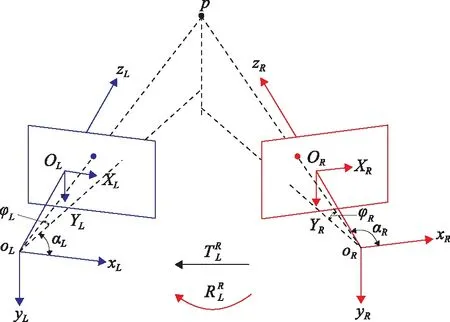
图2 双目相机的测量原理

在视觉测量的过程中，首选要对相机的内外参数进行标定。通过单相机的标定，可得到视场范围内任意点P在二维图像坐标系中的像素坐标(uP,vP)与世界坐标系中的坐标(xP,yP,zP)间的转换关系为

(1)

式中：K为相机的内参矩阵；H为相机的外参矩阵；fx为焦距长度与相机芯片每个单元x方向尺寸的乘积；fy为焦距长度与相机芯片每个单元y方向尺寸的乘积；cx,cy为相机的主点坐标；RC为像素坐标系与世界坐标系间的旋转矩阵；TC为像素坐标系与世界坐标系间的平移向量。

分别对左右相机进行标定后，通过立体标定得到左右相机的对应关系，利用空间交汇的原理，即可将视场内的任意空间点在左相机坐标系下进行重建，得到点在全局坐标系下的三维空间坐标。

按照上述建立全局坐标系的方法，将局部坐标系建立在局部测量系统的左相机上，并利用相同的标定方法，标定局部测量系统，从而可以获得空间内任意一点在局部坐标系下的三维坐标。

1.2 全局控制点的布局和匹配

为实现三维数据的全局拼接，需要在全局控制系统和局部测量系统的公共视场内设立具有公共信息的全局控制点，并根据这些点阵求解全局坐标系与局部坐标系间的转换矩阵。因此，全局控制点的建立对于全局三维数据拼接非常重要。传统的全局控制点布置方法需要根据被测零件的尺寸及形状，在测量视场中提前对全局控制点的放置区域及摆放密度进行设计，并由人工布置，前期准备工作非常繁琐，且在局部测量过程中，若部分点受到遮挡，会严重影响拼接的精度。

图3 柔性全局控制点

针对全局控制点布局的问题，本文提出一种柔性投影控制点的方法，如图3所示，利用局部测量系统中的投影仪，根据被测零件的表面特征，柔性投影特征点阵。其中，矩形外边框所围成的区域为局部测量系统的测量范围，用以保证局部测量的过程可以覆盖被测物所有的表面区域，边框内部投影的点阵作为全局控制点，充满整个视场。由于全局控制系统的两台相机距被测零件较远，若特征尺寸较小，受相机分辨力限制，相机的测量精度降低，因此，为了保证拼接的精度，投影的柔性控制点尺寸根据测量现场全局控制系统与零件表面的位置关系进行实时调整，使控制点占据尽可能多像素，提高点的提取精度，从而保证三维数据拼接的质量。

采用这种投影控制点的方法，柔性高，现场适应性强，省去了人工布点的繁琐工作，操作更加简便，且由于不需要在零件表面粘贴标记点，保证了零件的表面精度。此外，根据被测零件的表面特征可以实时调整投影点的位置，可以避免控制点被遮挡或变形，极大提高了数据拼接的精度和稳定性。

全局控制系统和局部测量系统分别采集控制点阵的图像，并在各自的坐标系下重建得到点阵的三维坐标。则局部坐标系下控制点集P={Pi|Pi∈P,i∈N,i≥3}，其中，Pi=(xi,yi,zi)为点Pi在局部坐标系下的三维坐标。全局坐标系下的控制点集为Q={Qi|Qi∈Q,i∈N,i≥3}，其中,Qi=(xi,yi,zi)为点Qi在局部坐标系下的三维坐标。

基于控制点的空间特征不变性对两点集中的控制点进行匹配。分别构建点集P和Q的描述向量。

Ai=|d(Pi,P1)d(Pi,P2)…d(Pi,Pn)|,n≠i

(2)

Bi=|d(Qi,Q1)d(Qi,Q2)…d(Qi,Qn)|,n≠i

(3)

式中：d(Pi,Pj)=‖Pi-Pj‖2，d(Qi,Qj)=‖Qi-Qj‖2分别为点Pi与P中其他点间的欧式距离和点Qi与Q中其他点间的欧式距离。

由于在控制点的提取和重建过程中误差的存在，相互匹配的点对的描述向量并不完全相同，因此需要设定一阈值φ，若点Pi和点Qi的描述向量满足

‖Ai-Bi‖2<φ

(4)

则认为点Pi和点Qi是相互匹配的，即(Pi,Qi)为匹配点对。最后，将P，Q中的点根据匹配关系重新编号排序，得到高精度匹配的控制点集P′={Pk|Pk∈P,k∈N,3≤k≤i}和Q′={Qk|Qk∈Q,k∈N,3≤k≤i}。

1.3 三维数据的拼接及优化

根据全局坐标系下与局部坐标系下对应的匹配点对，可求解全局坐标系与局部坐标系的坐标转换关系。对于空间中的这两个坐标系，同时存在旋转和平移，即同一控制点在两坐标系下的坐标可表示为

Qk=R·Pk+T

(5)

式中:R为坐标系旋转矩阵；T为坐标系平移向量。为方便计算，利用向量的计算先得到旋转矩阵之间的关系，然后再利用点的坐标计算平移向量，即

(6)

具体的求解过程为

首先，计算两匹配点集的质心点

(7)

(8)

其次，分别计算两匹配点集中的向量

(9)

(10)

则

(11)

建立目标函数

(12)

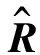
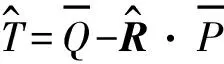
(13)

2 大型三维形面测量实验

图4 大型零件三维数据测量系统

搭建大型零件三维数据测量系统如图4所示，局部测量系统由两台工业相机(VC-12MC-M/C 65，焦距28 mm，分辨力3072×4096)和一台投影仪(EPSON，3000 lm)组成，全局控制系统由两台高精度大视场工业相机(VC-29MC-M/C，焦距50 mm，分辨力4384×6576)组成。根据1.1的标定方法，在实验室对两套双目相机组成的测量系统进行精确标定，并利用测量系统对大型零件进行了三维数据采集和重建。

在北极这样的寒冷地带生活，没有一些特殊本领怎么能行？一些苔藓可以在零下10℃的环境里生存，而地衣就更厉害了，即使是零下20℃的低温，它们也无所畏惧。苔藓和地衣都是紧贴着地面匍匐生长的，这其实是一种对付极寒天气的生存智慧，因为只有“趴在地上”，才能够抗风、保温，并且减少植物的蒸腾作用，更好地生存下去。

2.1 阶梯式全局测量系统的标定

根据双目系统测量视场的大小，基于张氏标定法，采用300×400 mm的黑白棋盘格标定板对局部测量系统进行标定，采用600×800 mm的黑白棋盘格标定板对全局测量系统进行标定，标定板的精度为0.02 mm。

1)复合式全局测量系统的系统参数标定

对全局控制系统即后双目系统进行标定，得到标定结果为

左相机内参：fx=8767.1,fy=8751.4,cx=3106.6,cy=2242.1,k1=0.10661,k2=-0.07177;

右相机内参：fx=8868.9,fy=8852.4,cx=3451.1,cy=2194.9,k1=0.066,k2=1.218;

对局部测量系统进行标定，标定结果为

左相机内参：fx=5206.1,fy=5208.4,cx=2053.9,cy=1527.6,k1=-0.026,k2=0.209;

右相机内参：fx=5177.0,fy=5185.5,cx=2138.3,cy=1497.2,k1=-0.026,k2=0.178。

根据1.1节，全局坐标系和局部坐标系分别建立在前后双目系统的左相机上。

2)局部坐标系与全局坐标系的转换

在局部测量的第一个测量站位，利用局部测量系统中的投影仪，在被测零件的表面投影全局控制点，控制点的分布根据被测零件表面的特征实时调整，保证尽可能多的点出现在相机视场中。

利用前后双目系统，分别采集投影的柔性控制点阵。根据控制点阵的空间不变性，前后双目系统两次采集得到的点阵中各点间的位置关系相对不变。利用式(12)和式(13)，求解得出局部坐标系与全局坐标系的转换矩阵。

按照规划的局部测量路径，移动局部测量系统到相应的测量站位，重复上述过程，并求取每一个位置下局部坐标系与全局坐标系的转换矩阵，将所有三维数据都统一到固定不变的全局坐标系中，即可实现大型零件的全局三维测量。

2.2 全局拼接方法精度验证实验

本文采用标准殷钢尺来验证阶梯式全局测量系统的测量精度，标准尺的长度为1100.0207 mm。其验证的过程为：将标准尺以不同的倾角放置在测量空间中相机的合焦平面周围，利用全局拼接系统分别测量标准尺两端的两个特征点A，B，并将两次测量到的数据转换至全局坐标系下，计算得到标尺长度，通过与标准尺的标准长度对比来评价本文提出的拼接方法的精度。

标尺的三维重建图如图5所示，各个端点的测量数据如表1所示。利用本文提出的拼接方法，重建一维标尺的最大误差为0.1593 mm，可认为其拼接精度为0.1593 mm，小于0.2 mm，具有很高的拼接精度。

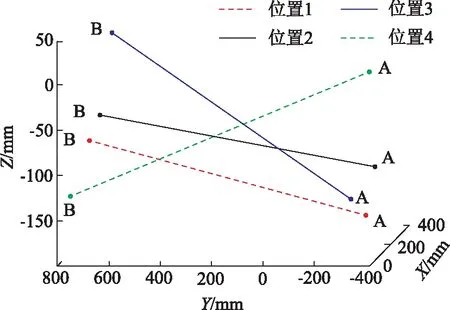
图5 一维标尺拼接重建

2.3 大型壁板拼接实验

采用本文提出的全局测量系统，在实验室中对已知数学模型的大型复合材料壁板进行拼接测量实验。根据壁板的尺寸，选取合适的三个测量站位，并在三个位置投影柔性全局控制点，计算获得三次测量的转换矩阵，如表2所示。使用局部测量传感器在每一个位置对壁板进行测量时，相机采集到的图像如图6所示。然后，将得到的每一个位置的三维点云数据统一到全局坐标系下，进而实现对大型壁板的三维拼接测量，拼接重建结果如图7所示。完成拼接后，三个站位所得到的测量点云之间不存在错位、旋转等问题，重建得到了被测壁板的三维型面信息。通过计算拼接点云数据与三维数模间的均方根误差(RMS)对拼接方法进行评价，测量点云数据与模型对应点间的均方根误差为0.4734 mm，同时对于该壁板件在三坐标测量机上进行测量，其测量结果与模型对应点间的均方根误差为0.254 mm，可以验证本文提出的方法对于复合材料壁板测量的有效性，可以满足大型壁板的测量要求。

图6 双目相机采集到的灰度图像

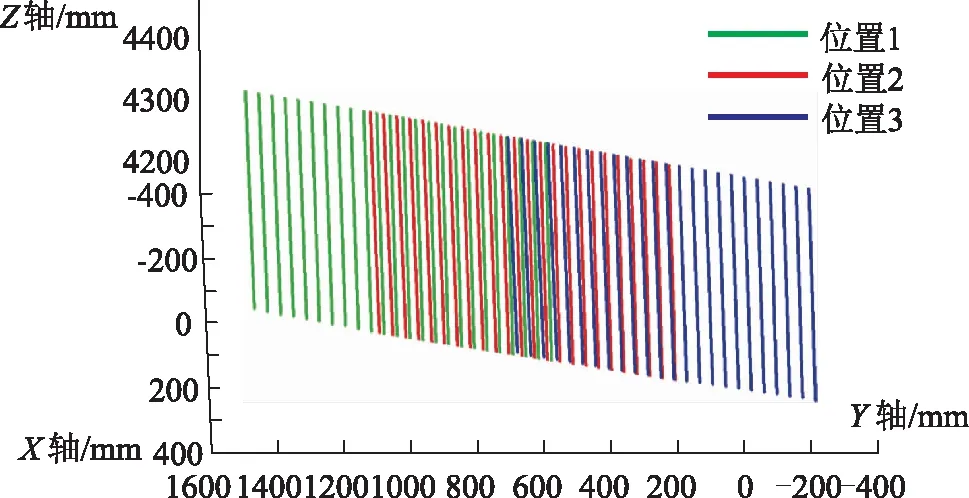
图7 大型复合材料壁板拼接点云

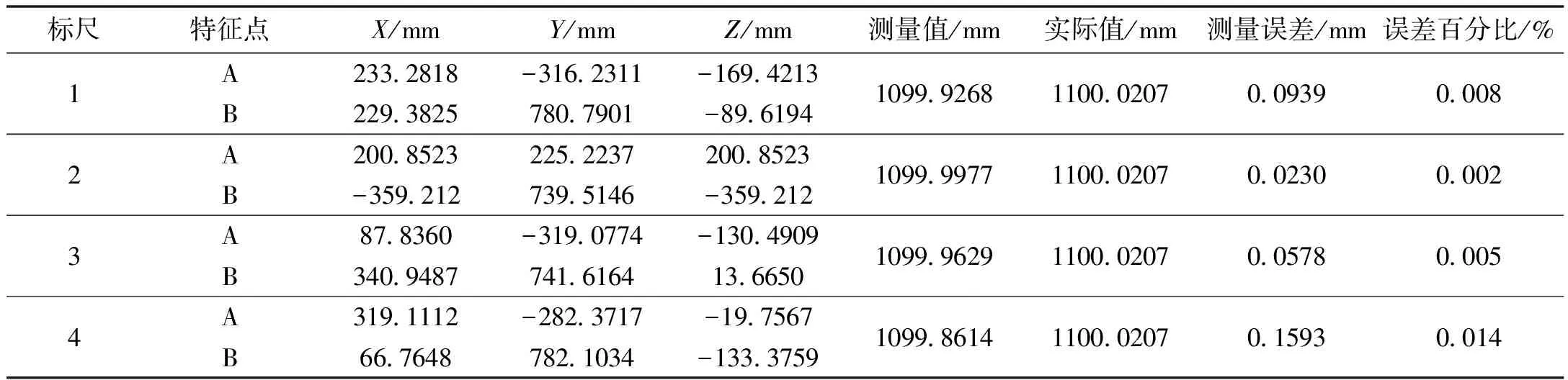
表1 不同位姿标尺拼接重建结果

表2 坐标系转换矩阵

3 结论

针对现有大型零件全局测量过程中存在的不足，提出一种基于柔性控制点的全局三维数据拼接方法。该方法利用投影柔性控制点，解决了传统大型零件测量过程中控制点布局繁琐、效率低的问题，提高了测量系统的现场适应性。采用阶梯式双目系统进行局部和全局的三维数据采集，便于测量过程中根据被测零件表面特征实时调整测量站位，保证公共视场中存在足够多的拼接控制点，提高了数据拼接的精度和测量稳定性。本文详细介绍了阶梯式三维数据拼接的原理和全局测量流程，在实验室中，利用定长标尺对拼接方法的精度进行了验证，在4000×3000 mm的测量视场范围内拼接精度可达0.1593 mm；此外，利用本文提出的三维数据拼接方法对大型复材壁板零件进行了多站位测量并进行了三维数据拼接和重建，重建结果显示该拼接方法可以满足大型零件的现场测量要求，验证了其有效性。