基于模糊控制的无人水面艇航迹跟踪控制

梅爱寒，李宝安，张法帅

(北京航空航天大学，北京 100191)

0 引言

无人水面艇(Unmanned Surface Vehicle，USV，简称无人艇)是一种可以在海洋中实现自主航行并完成相应任务使命的小型水面船舶[1]。无人艇的运动控制问题主要包括航速与航向控制、航迹跟踪、镇定、智能规划、避障与导航、多智能体协编队控制等[2]。船舶的实际运动异常复杂，一般情况下具有六个自由度。对于大多数船舶运动及其控制问题而言，可以忽略起伏、纵摇、横摇运动，而只需考虑前进、横漂和艏摇运动，简化为三自由度的水平面运动问题[3]。

无人水面艇航迹跟踪控制是指在无人艇整体系统的作用下，使无人艇从预定的起始位置沿着指定轨迹一直航行到达目的位置。已有的航迹跟踪控制可分为综合控制和分离控制两种方案，综合控制(直接式)方案同时接收航迹偏差和航向偏差，输出舵角控制指令；分离式(间接式)控制方案分为相互嵌套的3个环：外环航迹控制、中环航向控制、内环舵角控制。综合控制方案的航迹控制精度高，但系统调试难度大，运用灵活性不足；分离式方案中航迹和航向控制功能相对分离，便于两种控制模式相互转换，而且有利于采用软硬件模块化结构开发，缺点是控制精度略低。因此选择以分离式方案为基础，添加目标速度计算和速度控制器环节，提出新的航迹跟踪控制方案，优化控制性能。

1 无人艇航迹控制方案

航迹跟踪控制方案由两部分组成：一是分离式(间接式)控制方案，将控制分成相互嵌套的3个环，组成串级控制；二是速度环节，调节目标速度并进行速度控制，整体构架如图1所示。

外环(航迹环)的功能是将GPS接收的无人艇位置信息与目标航线进行比较，计算航迹偏差，通过航迹控制算法计算得到命令航向ψr(k)，将其给到航向控制环，引导船舶向着消除航迹偏差的方向驶进；

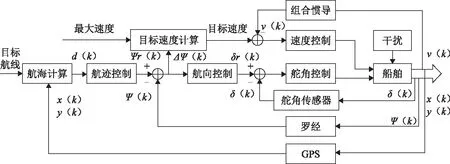
图1 航迹跟踪控制结构图

中环(航向控制环)将罗经采集的实际航向与目标航向比较得到航向偏差信号，经过航向控制算法得到一个命令舵角δr(k)给舵角控制环，使船艏向减少航向偏差的方向转动；

内环(舵角控制环)则用于驱动舵机使舵角检测值与目标舵角值一样[4]。

速度环节用于控制无人艇航行速度，首先目标速度计算模块根据最大速度和航向偏差计算目标速度，当转弯时则降低目标速度，当直线航行时则增加目标速度至最大速度；速度控制器将目标速度与检测到的速度比较得到速度偏差△υ(k)，经过速度控制器输出速度控制指令发给发动机，通过控制发动机转速来控制螺旋桨转速，从而间接控制航行速度。

2 无人艇运动数学模型

2.1 坐标系及符号定义

在描述水面船舶的运动时，一般采用两种不同的直角坐标系：大地坐标系OE-XEYEZE和船体坐标系Ob-XbYbZb，皆遵守右手法则，如图2所示。

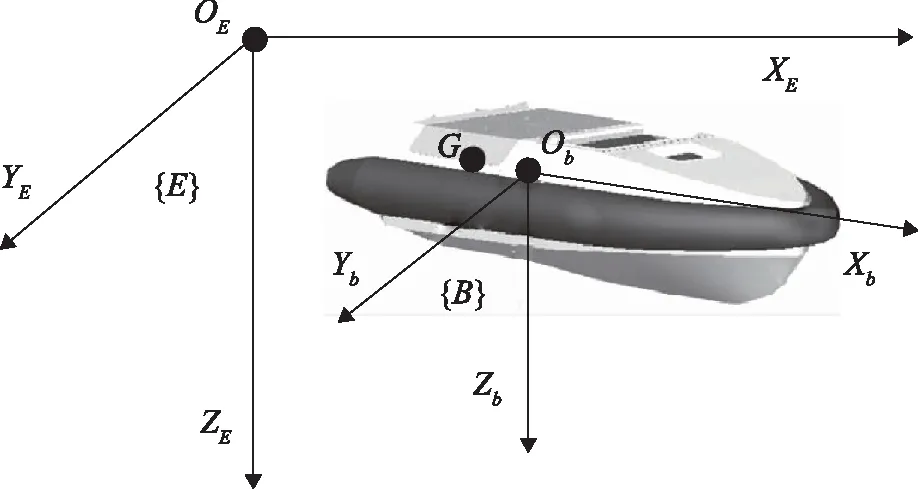
图2 坐标系说明

大地坐标系描述的是船舶的位置和姿态，船体坐标系描述船舶的速度和受力。船舶运动描述中所用的符号如表1所示。

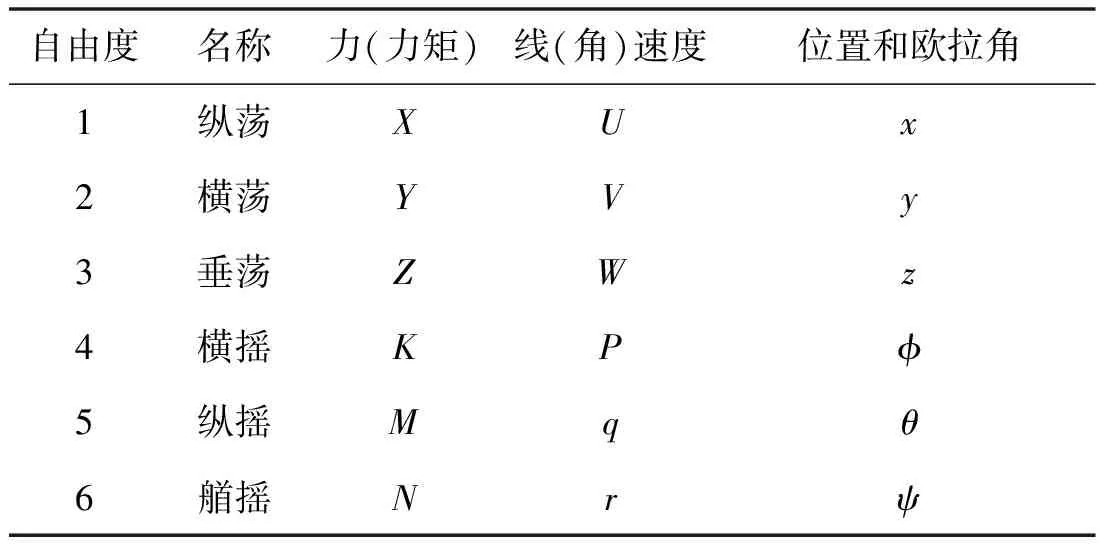
表1 符号体系说明

2.2 船舶操纵的线性化模型

把运动坐标系的原点选在船舶重心G上，并考虑到船舶的对称性，船舶在平衡位置作小幅度运动。船舶在舵作用下的运动基本上是一个质量很大的物体的缓慢的转首运动，于是用一个惯性环节来代表艏摇运动

(1)

式中:δ为舵角；ψ为艏摇角；T为稳定性参数；K为回转性参数；Nd为海浪、海风和海流对船舶的艏摇扰动力矩；N为回转中所受阻尼力矩系数。

式(1)称为一阶野本模型(Nomoto)方程，T和K被广泛的用来评价船舶操纵性的参数，它们可以通过船舶在海上做“Z”形试验和回转实验得到。本文采用是某4000 kg无人艇的模型，其中K=1.148，T=9.848。

2.3 船舶直线运动模型

假设：①无人艇是一个刚体；②大地参考系是惯性参考系；③水动力与频率无关，水的自由表面做刚性壁处理；④附体坐标系原点取在质心C。则

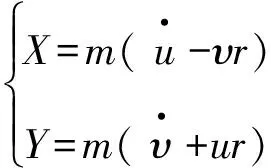
(2)

式中:X，Y为船舶在x，y轴上受的力；m为船舶质量；u为前进速度；v为横漂速度；r为艏摇角速度[5]。

3 控制器设计

控制结构如图1所示，共有四个控制器，分别是航迹控制器、航向控制器、舵角控制器和速度控制器。在实际海况中，由于实际船舶模型具有不确定性、非线性、非稳定性和复杂性，很难建立精确的模型方程，所以考虑使用智能控制方法。模糊控制能够利用人类专家控制经验，对非线性、复杂对象的控制有鲁棒性好、控制性能高的优点，所以决定采用模糊控制。

理论分析和试验表明，只利用模糊控制器进行系统控制，往往不能满足控制对象的所有指标(尤其在控制低层)，所以一个完整的模糊控制系统还需要某种传统的控制器作为补充，一般采用的就是PID控制方法。

基于以上考虑，决定将模糊控制和PID相结合。分离式控制方案使用航迹PID控制-航向模糊控制-舵角PID控制的方案，速度环节使用PID控制器。控制设计框图如图3所示。

图3 自控设计框图

3.1 PID控制器

使用PID设计航迹控制器、舵角控制器和速度控制器。PID控制是应用最广泛的工业控制器，位置式PID离散表达式

(3)

式中：T为采样周期；k为采样序号，k=1，2…；u(k)为控制器在第k时刻的输出值；e(k-1)和e(k)分别为第(k-1)和第k时刻所得到的偏差信号；kp为比例系数；ki为积分系数；kd为微分系数。

3.2 模糊控制器

采用模糊控制设计航向控制器，模糊控制包括四个部分：模糊化，规则库，模糊推理和解模糊[6]。

3.2.1模糊化与规则库

式(1)描述的是船舶转首运动，输入舵角，输出艏摇角。在仿真试验中计算航向偏差时，根据输出的艏摇角和当前目标航向角比较，得到航向偏差。如图3所示，分离式控制方案中航向控制器的输入为航向偏差，输出舵角值传递给舵角控制器。

航向模糊控制器选择船舶航向偏差E和航向偏差变化率EC作为输入变量，舵角值U作为输出变量。

参数的基本论域:航向偏差e为[90°,-90°]；航向偏差变化率ec为[-3.2°/s,3.2°/s]；全量舵角u为[-35°，35°]。航向偏差的真实范围为[180°,-180°]，考虑在实际航迹跟踪中，设计航线时相邻航线的角度偏差基本小于90°，为了提高控制的精度，缩小航向偏差录入的范围，若超过范围则赋边界值。

根据船舶操纵以及控制器设计的需要，模糊变量的量化论域为E：X={x∈Z|-75≤x≤75}，EC：Y={y∈R|-64≤y≤64}，U：Z={z∈R|-14≤z≤14}，为了提高控制精度，故量化论域的个数较多，对应的控制精度为dE=1.8°，dEC=0.075°/s，dU=5.25°。

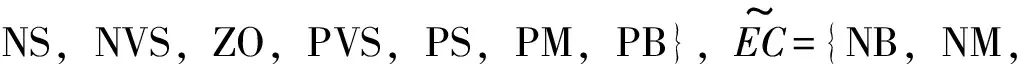
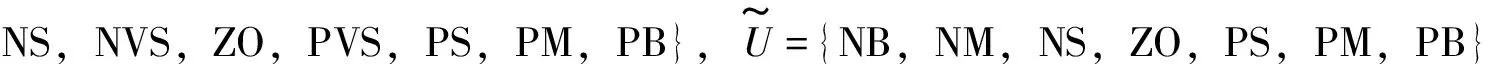
由控制规则可以看出建立模糊控制规则的基本思想。考虑偏差为正的情况，当偏差较大(PB，PM)且偏差变化率为正或负小时(不是NB)，为了尽快消除偏差，选择较大的舵角输出(PB)；当偏差较大(PB，PM)且偏差变化率为负大时(NB)，这时偏差减小的很快，为了防止超调，选择零舵角(ZO)；当偏差较小(ZO，PVS)且偏差变化率为负大时(NB，NM，NS)，为了减小变化的趋势，防止超调，选择较大的左舵(NM)；当偏差较小(ZO，PVS)且偏差变化率较小时(NVS，ZO)，使用较小的舵角(NS，ZO，PS)，使系统快速稳定。其他情况的控制规则类似，模糊规则的三维图如图4所示。

表2 航向模糊控制表

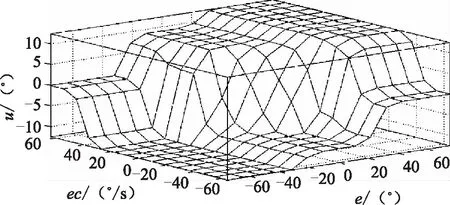
图4 模糊控制规则表三维图

3.2.2模糊推理与解模糊

航向控制系统是两个输入一个输出的模糊控制器，在控制器设计中与运算用求交法，或运算用求并法，模糊蕴涵用乘积法，模糊规则综合运算用求和法。

解模糊处理选用面积重心法(加权平均法)，取模糊推理得到的隶属度的加权平均值。

(4)

式中:μC(x)为通过模糊推理得到模糊集合C′的隶属函数[7]。

4 仿真结果和分析

在直角坐标系下，定义x轴为正东方向，y轴为正北方向，航向角为沿y轴正半轴顺时针转动的角度，角度范围为[0,360)。设计航线，共计7个航点，具体航路规划信息如表3所示。

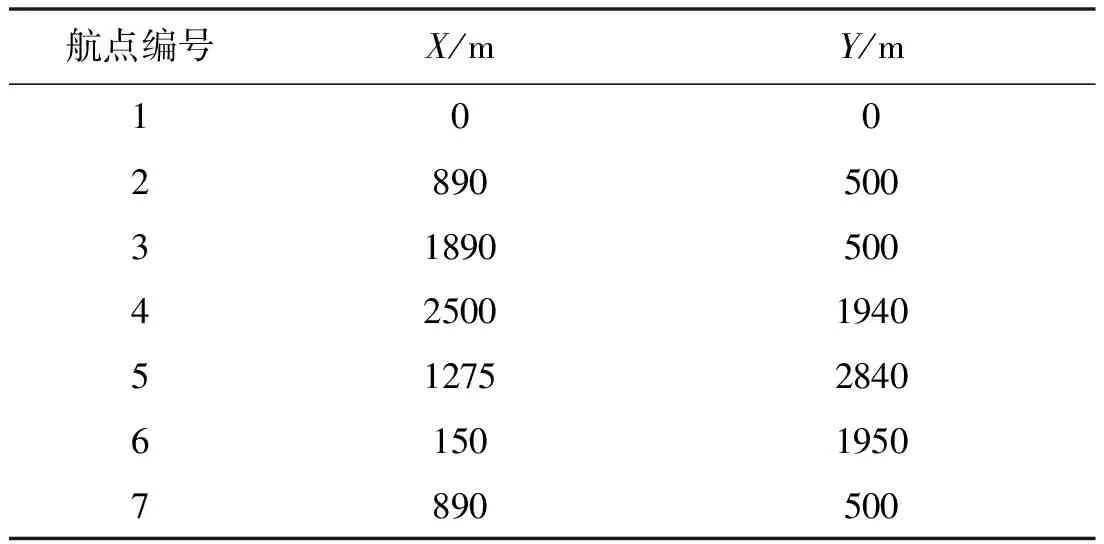
表3 航路规划航点信息

4.1 无干扰条件情况下航迹跟踪试验

初始条件为：初始位置(0,0)，初始航向角为0°，初始速度为0 m/s，在无干扰条件下，进行仿真试验，结果如图5所示。

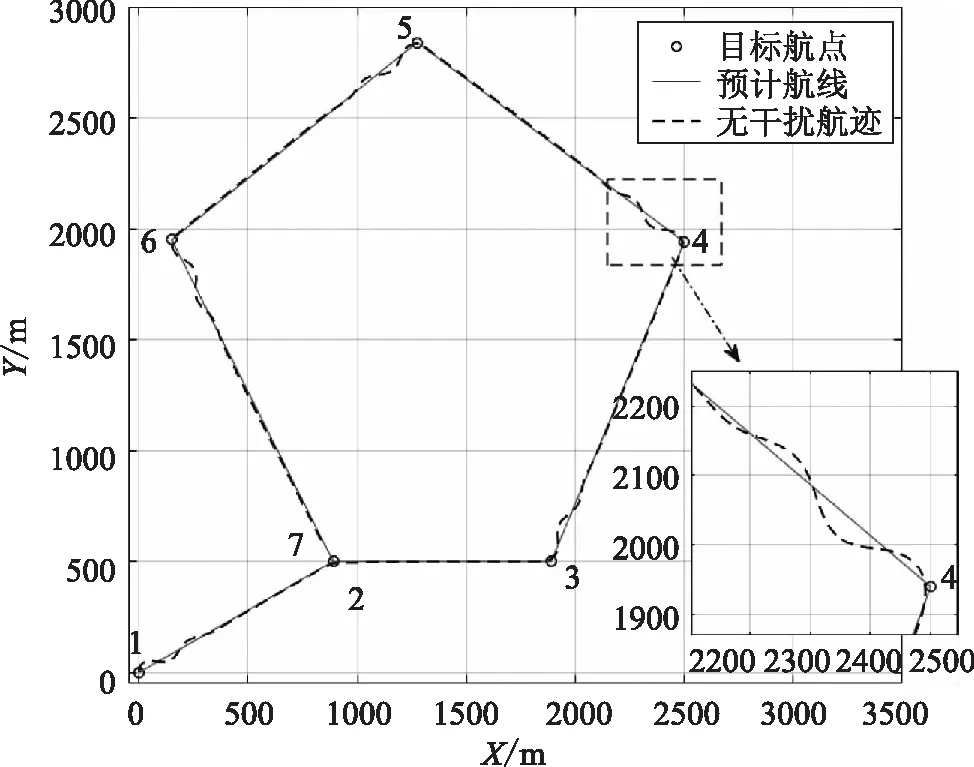
图5 无干扰情况下航行轨迹

由图5可以看出，无人艇从初始位置出发右转沿着60°的航线航行，然后右转进入90°的航线，沿着五边形的航线逆时针航行，最终抵达终点。全程航迹跟踪没有发生航路偏离，直线行驶平稳，拐角转弯过渡自然。

从第4个航点的局部放大图中可以看出，抵达目标航点后切换新的目标航点和航线，经过2次震荡后侧偏距小于5 m，跟踪新航线成功。在预计航线中，每抵达一个航点后切换目标航线，航迹控制器控制无人艇向新的目标航线航行。经统计在控制中最大偏差值为30.5 m，调节时间约为35 s，稳态误差在±5 m内，航迹控制器整体具有良好的稳定性、快速性和准确性。

4.2 有干扰情况下航迹跟踪试验

在海洋中航行的的干扰可以分为两类：固定干扰(稳流风、海流等)和随机干扰(湍流风、海浪等)。设置固定干扰方向为135°，影响速度大小1 m/s；随机干扰为正弦信号，幅值为±2 m/s，方向135°，周期为200 ms，其余初始条件均与无干扰情况相同，结果如图6所示。

由图6可知，有干扰情况下第4段和第6段航线上航行较为稳定，波动较小。这是由于第4段是顶浪航行，第6段为顺浪航行，与干扰方向接近，侧面受到的干扰较小；其余航线上由于侧面受到干扰作用，无人艇会偏离航线，在航迹控制器的作用下，不断调节，因此均有不同幅度的波动。进入稳定震荡状态后，侧偏距震荡的幅度小于20 m。航行控制器在受到干扰的情况下，仍能实现跟踪航迹功能。

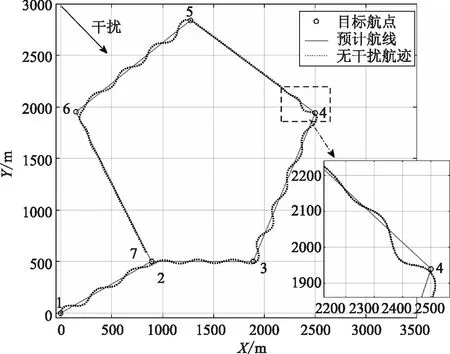
图6 有干扰情况下航行轨迹

4.3 K,T参数修改

由于船舶在复杂的海洋环境中运动，模型具有线性、不确定性等特性。船舶操纵方程中的K，T参数在实际工作中会随船速、吃水深度、状态等变化而在一定范围内变化，所以进行鲁棒性实验，在实验中修改K，T参数，观察控制效果。

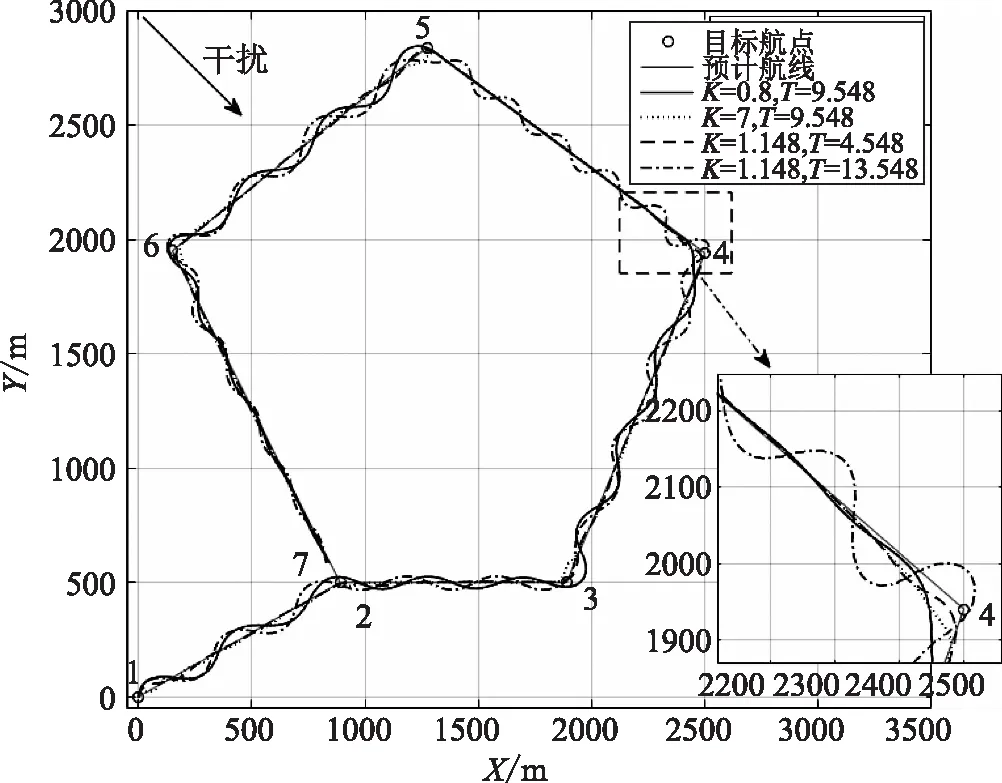
图7 有干扰情况下K，T参数改变的航行轨迹

K取0.05至11内的数值，T取1至20范围内的数值。选取大量不同K，T参数，干扰条件和初始条件均与有干扰情况下条件相同，结果如图7所示。

图7显示了四种典型K，T参数的航迹。在不同的参数和干扰下，仍能完成航行控制任务，当T值较大和K值较小时，航行过程中波动较大。在分离式的航迹控制方案中，采用模糊控制作为航向控制器具有良好的鲁棒性，针对模型参数变化仍能有较好的控制效果。

5 结论

本文提出新的航迹控制方案，在间接式航迹跟踪的结构上添加速度控制，通过速度控制能够自然地完成转弯运动，经过仿真表明该方法能够准确、快速的跟踪目标航迹。航向控制器采用模糊控制，具有良好的鲁棒性、适应性强，在有干扰和参数变化的情况下仍能达到控制要求。新提出的航迹控制方案和仿真验证为以后构建更加完善的仿真平台和进行实际水面实验奠定了基础。