某型舰载靶弹射击诸元解算方法研究∗

（91851部队 葫芦岛 125001）

1 引言

靶弹在舰载发射时，会受到起飞平台姿态信息影响，因为载舰在航行时姿态是时刻变化的，靶弹的发射方向不能对准目标方向或者不能按照理论射向，靶弹指挥仪的任务就是控制靶弹向预定方向准确发射［1］。因此，靶弹指挥仪必须能够精确地解算出靶弹的射击诸元，并将解算结果实时地向靶弹装定，控制靶弹向预定方向发射。要精确地求解靶弹的射击诸元，需要找出靶弹射击诸元与载舰、目标运动特性、气象环境信息及靶弹的性能参数之间的关系，并利用合理快速的算法具体计算出靶弹的射击诸元。

某舰载靶弹采用前置点射击方式，即考虑在靶弹飞行时间内假想目标的运动，向假想目标的前置点发射靶弹［2］。本文根据靶弹的射击特性建立靶弹的射击方程，通过对载舰运动的修正得到准确的目标参数，最后利用梯度算法求解超越方程。实践表明，此种方法可以较精确地计算靶弹的射击诸元。

2 靶弹射击模型

在研究靶弹在运动载舰射击模型时，需要对载舰、目标和环境等条件进行一定的假设，假设条件如下［5］：

1）假定载舰和目标均作匀速直线运动，载舰航速、载舰航向、目标距离、目标速度均为已知。

2）我舰舷角由舰上雷达测得，雷达天线与发射装置之间的距离比目标距我舰的距离近得多，因此认为雷达天线与发射装置在一点上。

3）靶弹自控飞行的海域内，风速风向不变。即导弹自控飞行时，仅受常值风的干扰。

在上述假设条件下，射击方程建立的思想是使靶弹飞行到自控段终点时，其弹体轴线正好对准目标，与目标的水平距离正好等于装定的自导头作用距离［6～7］。由于受到载舰运动姿态影响，靶弹发射瞬间不能指向目标方向，靶弹发射后弹道会有一个扇面角。定义坐标系如下：

靶弹发射坐标系OX1Y1Z1：OX1轴正向为靶弹发射时弹轴指向，OY1轴铅垂向上，OZ1轴与X1OY1平面构成右手系。

靶弹弹道坐标系OX2Y2Z2：靶弹扇面转弯完成后的平直弹道为OX2轴，OY2轴铅垂向上，OZ2轴与X2OY2平面构成右手系。

靶弹飞行几何关系图如图1所示。

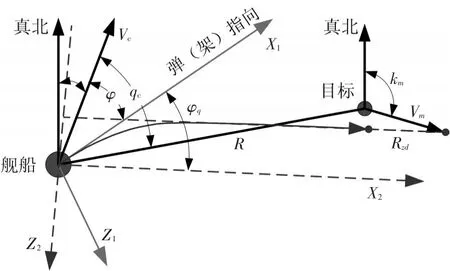
图1 靶弹飞行几何关系图

图中，R为目标距离，Rzd为靶弹装定的自导头作用距离，kc为我舰航向角，Vc为我舰航速，km为目标的航向，Vm为目标航速，φ为靶弹发射架安装角，qc为我舰舷角，φq为靶弹发射扇面角。根据几何关系，在靶弹弹道坐标系中建立顺航向和正交航向的路径方程如下：

式（1）中tzk是靶弹自控飞行时间，Rzd是装定的自导距离。将式（2）带入式（1），可以得到在X1OZ1坐标系下的射击方程：

3 载体运动修正

在射击方程中，qc是雷达测得的我舰舷角值，它应该是地理坐标系中的舷角值。由于雷达是装在载舰上，当载舰摇摆时雷达天线轴会随着摆动，因而测得的我舷角值也随着载舰运动而变化，对此必须进行修正，修正的原理是找出载舰运动后的坐标系与载体运动前的坐标系之间的关系［8～9］。

假设载舰稳定时，其坐标系为OXcYcZc，OXc轴为载舰纵轴，OYc轴在垂直平面内垂直OXc轴，OZc轴垂直OXcYc平面构成右手系。

图2 载舰运动前后坐标系

两坐标系之间的关系式为

从上式中可以看出，只要测出目标在载舰运动后坐标系内的舷角及俯仰角，就可以根据载舰摇摆角度进行数据修正，得出目标在稳定地理坐标系内的舷角。

4 超越方程求解算法

在式（3）中，X1、Z1分别为靶弹在发射坐标系中自控段终点的纵向距离和侧向距离，如果能得到X1、Z1，解联立方程（3）就能得到靶弹射击诸元 φq、tzk的值。

X1、Z1与靶弹发射扇面角、飞行时间、靶弹速度、风向、风速、载舰速度等诸因素有关，但每个因素对其影响的大小并不相同，可以用正交试验设计的方法来安排计算标准弹道，然后用多项式回归分析方法得到一定精度条件下表达形式较为简单的弹道回归方程，弹道方程形式为

t、φq、T 、VF、VJ分别为靶弹飞行时间、发射扇面角、当前大气温度、风速、载舰航速。假设风向（风尾与真北的夹角）是kf，把风速分解到OX1轴和OZ1轴上为

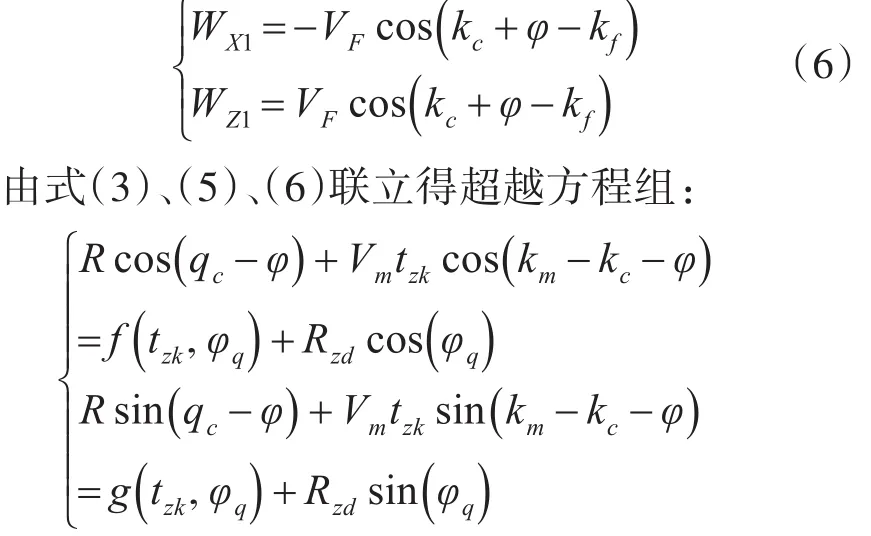
上述超越方程中只有tzk和φq是未知的，可以通过数值解法求解，本文采用梯度法计算［3～4］。设VPJ为飞行器平均速度，tzk，φq的初值t0，φq0为

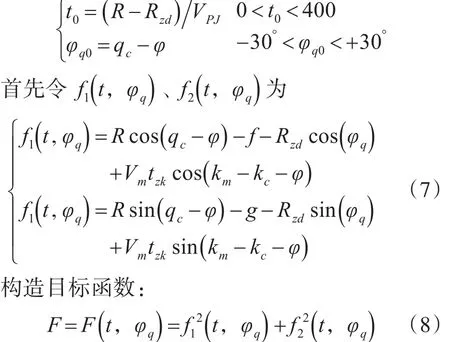
计算F(t0，φq0)。若F ＜ ε（ε为设置的精度），则此时t0，φq0即为求解的自控时间和扇面角；若F＞ε，则进行以下步骤：

计算目标函数F对t，φq的偏导数：

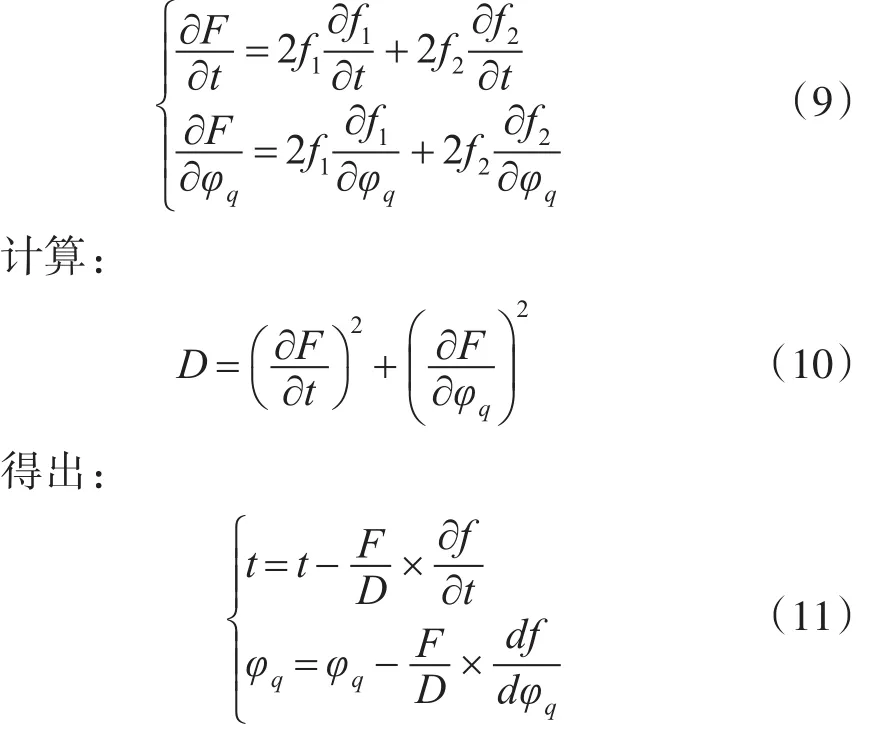
式（7）～（11）反复迭代，直至满足F＜ ε条件时得出足够精度自控飞行时间tzk和发射扇面角φq。

5 结语

本文根据某舰载靶弹射击时载舰、目标、靶弹的特性及控制原理，建立了靶弹的射击方程，分析推导了载舰运动时雷达测得我舰舷角的修正模型，最后利用梯度法求解超越方程得出射击诸元。实践表明，该方法迭代收敛速度快，可以快速、精确地计算出射击诸元，是求解靶弹射击诸元的一种有效方法。