靶弹系统纵向通道模型预测控制
2018-04-02陈家斌宋春雷
董 哲,陈家斌,宋春雷
(北京理工大学 自动化学院,北京 100081)
tracking
靶弹是为导弹提供目标的飞行器,其系统模型类似于导弹系统。在靶弹飞行器的控制过程中,对靶弹飞行轨迹的控制是控制系统的重要目标,而靶弹系统多参数、多扰动以及强耦合的特点为其控制带来了巨大难题。因此在处理靶弹系统时,常将靶弹系统运动分为水平通道与纵向通道分别研究,以实现对系统模型的简化。一般靶弹供靶轨迹可分为上升段、下降段与平飞段,各阶段因飞行高度、飞行特征不同加以区分,其中纵向通道即高度通道对靶弹性能影响更大,其直接决定了靶弹能否实现预期供靶轨迹[1]。
传统的靶弹飞行控制多是基于PID控制,其鲁棒性较差,对模型的精度要求较高,因此在此基础上,多结合自适应控制、智能控制算法[2]。近年来,H∞算法、滑模控制算法开始逐渐应用于靶弹系统控制,较好地增加了系统的鲁棒性,减少了对系统模型的依赖[3-4]。
预测算法是一种基于模型的算法,其已经广泛应用于工业、冶金等方面[5]。近年来,预测算法得到不断改进,文献[6]将系统局部线性化,结合鲁棒约束下的模型预测控制,得到了更好的预测结果;文献[7]采用模型预测控制与分段容许控制相结合的方法,解决了系统中的模型不确定问题和在线预测不准问题,扩大了预测控制应用范围。
模型预测算法主要包括预测模型、滚动优化与反馈校正3部分。预测模型的建立是控制的基础,在此过程中需要通过数学方法对系统原始模型进行处理;利用反馈线性化可以得到系统的能控标准型,通过设定合理的指标函数,可得到系统的模型预测控制器;滚动优化环节,能保证获得系统的局部最优解,并通过反馈校正,对系统预测结果不断优化,从而得到最终控制结果。
1 系统模型
为研究方便,现基于靶弹建立如下坐标系:取靶弹的质心为原点O,x轴与靶弹的纵轴向重合,指向弹头方向为正;z轴垂直于靶弹纵平面指向靶弹两侧,从弹头方向看去,向左为正;y轴与x、z轴遵循右手螺旋定则,指向上为正[8]。
在建立纵向通道运动方程前,为方便研究,首先做出如下假设[9]:
1)忽略靶弹飞行过程中的形变;并忽略地球曲率的影响。
2)重力加速度的值为常值,且不随飞行高度而变化。
3)靶弹质量分布均匀,且为面对称,对称面为弹体坐标系的Oxy面。
4)在未受到扰动的情况下,设靶弹参数β、γ、v、ωx、ωy的变化相对于控制量是连续微小量。
5) 靶弹在飞行过程中水平机动较小,其弹体基本保持在某一纵向铅垂面内。
在设计靶弹方案飞行弹道的过程中,其运动参数选为俯仰角ϑ、攻角α、弹道倾角θ与高度h。靶弹纵轴与水平面之间的夹角为俯仰角ϑ;靶弹的速度矢量在弹体纵向对称平面内上的投影与Ox轴间的夹角为攻角α;靶弹速度矢量与水平面之间的夹角为弹道倾角θ;高度h选取为弹体相对于地面坐标系之间的高度[10]。
根据上述假设,结合系统参数,可以得到靶弹系统在此坐标系下的纵向运动方程:
(1)
式中:m为靶弹在任意时刻的质量;P为靶弹发动机推力;v表示靶弹系统的飞行速度;X、Y分别为靶弹在Ox轴方向与Oy轴方向受到的空气阻力;x、y分别为靶弹此时刻的位置坐标;Jz为绕z轴转动惯量;Mz为相应的z轴力矩;φ1为纵向通道控制误差,理想条件下,其值应为0。
在纵向通道设计过程中,采用“瞬时平衡”假设,即将靶弹看成质点进行研究,这样,靶弹质量可以表述为
m=-kt+m0
(2)
式中:m0表示系统初始质量;k为单位时间靶弹消耗的燃料质量。
同时引入靶弹的空气动力参数,这样可对上述方程可以进行进一步简化:
(3)
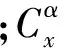
这样就得到了在靶弹坐标系下的弹体纵向通道运动方程,为了保证靶弹飞行平稳,延长供靶时间,减小高度误差,提高供靶质量,对靶弹上升段采用指数高度规律设计方案弹道:

(4)
式中:y*(t)为指令飞行高度;yp为靶弹高度调节变量,其大小决定了靶弹上升段与下降段的高度;y0为靶弹平飞供靶时的飞行高度;t1为靶弹预期平飞时间;k为控制系数。
平飞段是靶弹供靶的关键阶段,因此,对平飞段指令弹道的设计是靶弹飞行方案设计的重点部分。对于某一型号的靶弹,其平飞段要求能实现等速等高飞行,结合文献[11],设计平飞攻角为

(5)
在靶弹运动方程组中,对相应参数进行变换:
(6)
得到系统的状态方程:
(7)
取靶弹在纵向通道的位置坐标为系统输出,从而得到系统状态空间方程[12]:
(8)
系统的约束方程如下:
(9)
通过反馈线性化实现对上述状态方程的线性化处理和各通道之间的解耦:
(10)
L=Q+Hu
(11)
(12)
(13)
通过上述变换过程,可以得到靶弹纵向位置控制系统的状态方程与输出方程。
(14)
经过反馈线性化得到的此状态空间方程,被解耦成为相互独立的控制通道。
2 模型预测控制器设计
对于模型预测控制,其控制率的确定需要有相应的指标函数,对于一般的状态空间系统有:
(15)
x、u、y分别为系统的状态向量、控制向量和输出向量。对于任何确定的系统,其模型预测控制的指标函数通常可选为如下模式:

(u(t′)Ru(t′))dt′
(16)
式中:Q为误差权矩阵;R为控制作用权矩阵;单次预测时长为Tp;预测步长为t′。
在ti时刻,系统的状态为x(ti),经过时间t′,系统状态转变为x(ti+t′|ti),在这里有t′ 对于本文中的模型,传统的代价函数没有体现出系统对不同状态下的位置的跟踪效果,尤其是靶弹的平飞段,需要使靶弹能在预定的飞行高度飞行,并保持一定的时间。因此需要在反馈优化过程中,考虑到靶弹系统对方案弹道的跟踪,故对系统的性能指标做如下改善[13]: y(ti+t′|ti))+(u(t′)Ru(t′))dt′ (17) 式中,误差矩阵取为单位矩阵,y*(t)为靶弹预定飞行高度,其值可以通过式(4)得到,系统在ti时刻经过预测t′时间之后的输出表示为y(ti+t′|ti)。 通过比较式(16)与式(17)可知,新的指标函数J与传统的指标函数J0相比,增加了对靶弹预测位置与方案弹道之间的误差追踪,综合考虑了系统的输入,并结合了靶弹在平飞段的精度要求,对系统跟踪误差定义为 e(ti+t′|ti)=y(ti+t′|ti)-y*(ti)= Cnx(ti+t′|ti) (18) (19) 将式(17)带入(16)中系统性能指标中,于是得到: u(t′)Ru(t′)dt′ (20) 对预测控制中的某一阶段,取其阶段代价函数: Qx(ti+t′|ti)+u(t′)Ru(t′)dt′ (21) 控制量u的取值范围为实数范围内所有有界函数,通过对代价函数的不断反馈优化,最终得到控制率[14]: (22) 由式(22)可以解算出当0≤t I=|y*(ti)-y(ti+t′|ti)|≤I0 (23) 为了实现靶弹系统对方案弹道的跟踪,需要实时对靶弹所处高度与方案弹道要求的飞行高度相对比,从而得到当前时刻靶弹系统的误差信息。根据靶弹自身平飞时的飞行速度以及气动参数,可以确定靶弹纵向机动过载及时间参数,并由此确定靶弹距离误差上限I0。通过对靶弹系统预先分析,得出靶弹上升段、下滑段与平飞段的时间,并由此确定预测控制中的预测步长t′与预测区间Tp和控制时域Tc,初始发射角为ϑ0,以上参数构成靶弹系统初始状态。供靶问题中,靶弹需要的平飞高度及供靶时间共同决定了靶弹平飞供靶段参数。 模型预测控制参数选取如下: 对靶弹系统的仿真如图1、2所示,图1为靶弹系统的纵向通道的方案弹道,图2为基于模型预测控制下的位置跟踪曲线。 为了实现对不同型号导弹特征弹道的模拟,靶弹的上升段、下滑段与平飞段均需持续一定时间;从图1可以分辨出,靶弹系统各阶段区分明确,平飞时其高度为4.376 km,供靶段持续时间较长,飞行平稳,上升段时间大约30 s。下滑段无明显超调。其平飞高度、平飞供靶时间符合预期要求。各阶段均能满足不同型号的靶弹对目标的要求,控制结果较为理想。 从图2中对靶弹位置的跟踪可以看到,通过模型预测控制,可以使系统能迅速跟踪到方案弹道,在纵向通道上取得了较好的时间响应。从图中可以看出,控制系统对方案弹道的跟踪,响应较为迅速,在10 s左右能实现对控制信号的跟踪。稳定状态下的位置跟踪误差为0.120 7 m,这一控制结果满足靶弹系统控制要求。 为了验证系统稳定性,尤其是在外界干扰下的鲁棒性,向靶弹系统中加入噪声干扰,此噪声被添加至预期弹道中。将此情形下的仿真结果与PID控制下的仿真结果对比,如图3、4所示。 从图3中可以看出,当采用PID控制算法时,加入噪声后,靶弹系统位置会出现很大震荡。虽然从仿真图上看,系统最终能保持平飞,但是在实际情况中,由于靶弹自身过载有限,系统无法在强烈的振荡作用下保持平衡,因此,采用PID算法得到的系统是不稳定的。 而图4显示,当施加噪声影响后,采用模型预测控制的系统,仍旧保持了较好上升段与下降段:靶弹在60.14 s时转入平飞段,此时的平飞高度为4.496 km,相对于未引入噪声的情况,其平飞高度虽然受到影响,但是仍然满足供靶要求。相比较于传统的控制方法,其在供靶质量和时间上都有着很大改进,且都符合供靶目标。仿真结果证明,模型预测算法对于靶弹供靶轨迹控制方面有着较好的效果,且其系统鲁棒性相比于经典控制方法有了较大的改善。 笔者通过对靶弹系统纵向通道建立预测控制模型,并对其采用反馈线性化方法,实现了对纵向通道各个参数的解耦,建立了靶弹系统的纵向通道控制模型,通过考虑供靶目标,建立了新的预测代价函数,对供靶过程中各阶段需求进行了分析,并以此设计了靶弹飞行方案弹道。依照方案弹道设计了靶弹模型预测控制算法,仿真结果表明,模型预测算法较好的实现了靶弹方案弹道飞行与供靶目标,动态响应和静态响应结果均符合靶弹供靶要求,具有较好的稳定性与鲁棒性。 参考文献(References) [1] 袁俊.浅析巡航导弹防御及武器系统发展[J].制导与引信,2008,29(3):12-17,21. YUAN Jun. An elementary introduction to the anti-cruise missile defense and weapon system development[J]. Guidance & Fuze, 2008, 29(3):12-17,21.(in Chinese) [2] 王玮,吴晓燕,陈治湘.某型导弹俯仰运动非线性最优滑模控制器设计[J].弹道学报,2008,20(4):69-72. WANG Wei, WU Xiaoyan, CHEN Zhixiang. Design of non-linear optimal sliding mode control for pitching movement of missile[J]. Journal of Ballistics,2008, 20(4):69- 72.(in Chinese) [3] 李林静,刘永善.基于自适应控制理论的自动驾驶仪设计[J].战术导弹控制技术,2004(3):13-16. LI Linjing, LIU Yongshan. Design of autopilot on the basis of the adaptive control theory[J]. Control Technology of Tactical Missile, 2004 (3):13-16.(in Chinese) [4] 李友年,贾晓红,王海波.H∞控制理论在空空导弹自动驾驶仪设计中的应用[J].航空兵器,2004(6):12-15. LI Younian, JIA Xiaohong, WANG Haibo. The application of H∞ control theory in air-to-air missile autopilot design[J]. Hangkong Bingqi, 2004(6): 12-15.(in Chinese) [5] SILANI E,LOVERA M. Magnetic spacecraft attitude control: asurvey and some new results[J]. Control Enginee-ring Practice,2005, 13(3): 357-371. [6] SHAMAGHDARI S, NIKRAVESH S K Y , HAERI M.Integrated guidance and control of elastic flight vehicle based on robust MPC[J].Robust Nonlinear Control,2015,25(15):2608-2630. [7] YAO Y,YANG B,HE F,et al. Attitude control of missile via fliess expansion[J]. IEEE Transaction on Control Systems Technology, 2008,16(5):959-970. [8] 王洪强.某滑翔增程靶弹弹道设计与控制系统研究[D].上海:上海交通大学,2012. WANG Hongqiang. Trajectory design and control system research of rang-extended target missile[D]. Shanghai:Shanghai Jiaotong University,2012.(in Chinese) [9] MANIKONDAV,ARAMBEL PO, GOPINATHAN M, et al.A model predictive control-based approach for spacecraft formation keeping and attitude control[J].American Control Conference, 1999(6):4258-4262. [10] 盖俊峰,赵国荣,周大旺.刚体飞行器姿态机动的模型预测控制方法[J].弹箭与制导学报,2015,35(2):5- 9. GAI Junfeng, ZHAO Guorong, ZHOU Dawang. A model predictive control method for rigid aircraft attitude maneuver[J]. Journal of Projectiles, Rockets, Missiles and Guidance,2015,35(2):5-9.(in Chinese) [11] 李新国,方群.有翼导弹飞行动力学[M].西安:西北工业大学出版社,2005. LI Xinguo, FANG Qun. Winged missile flight dynamics[M].Xi’an: Northwest Polytechnic University Press,2005.(in Chinese) [12] 孙光,霍伟.卫星姿态直接自适应模糊预测控制[J].自动化学报,2010,36(8):1151-1159. SUN Guang, HUO Wei. Direct-adaptive fuzzy predictive control of satellite attitude[J].Acta Automatica Sinica,2010,36(8):1151-1159.(in Chinese) [13] 张邦楚,韩子鹏,范雁飞.巡航导弹模拟靶平飞弹道设计[J].弹道学报,2003,15(2):28-33. ZHANG Bangchu,HAN Zipeng, FAN Yanfei. Design of cruise missile simulated target[J].Journal of Ballistics, 2003,15(2):28-33.(in Chinese) [14] 陈海建, 滕克难,李波. 基于模糊理论的导弹系统贮存可靠性仿真方法研究[J]. 弹箭与制导学报,2011,31(2):33-36. CHEN Haijian, TENG Kenan, LI Bo. The research of missile reliability simulation methods based on fuzzy theory[J].Journal of Projectiles,Rockets,Missiles and Guidance,2011, 31(2):33-36.(in Chinese) [15] 甘旭升, 端木京顺, 张小花. 导弹自动驾驶仪的模糊自整定免疫PID控制[J]. 火力与指挥控制, 2007, 32(6):70-73. GAN Xusheng, DUANMU Jingshun, ZHANG Xiaohua. Design of missile autopilot based on fuzzy self-tuning immune PID control[J].Fire Control and Command Control,2007, 32(6):70-73.(in Chinese)



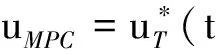
3 仿真结果与分析
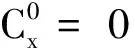
4 结束语
