位势Burgers方程的自相似解和行波解
2019-01-02林府标张千宏
林府标,张千宏
(贵州财经大学数统学院,贵州 贵阳 550025)
1 研究背景及现状
考虑众所周知的Burgers方程
vt+vvx=σvxx,σ>0.
引入位势函数φ(t,x)满足v=φx,则把变换v=φx代入Burgers方程,关于x积分并令积分常数为零,得
(1)
作变换
则方程(1)变为
为了简单起见,研究方程(1)不妨只需考虑下面的方程:
ut+(ux)2=uxx.
(2)
文献[1]讨论了位势Burgers方程(1)的对称.作变换g=-u,则方程(2)变成gt=(gx)2+gxx.文献[2]给出了该方程的一部分对称,文献[3]给出了该方程的所有对称.自然科学和工程中的许多问题都可以用非线性偏微分方程来描述,这些偏微分方程只有很少一部分可以解析求解,而偏微分方程的精确解析解可以帮助验算和估计数值解、近似解析解的正确性及误差,因此,非线性偏微分方程的精确求解及其解法研究作为非线性科学中的前沿研究课题和热点问题,极具挑战性.目前虽然已经提出和发展了许多求非线性偏微分方程解析解的技术和方法,但因为求解非线性偏微分方程不可能有普遍而统一的理论方法,继续寻找一些有效可行的求解方法依然是一项十分重要和有价值的工作.
随着李群在偏微分方程中的广泛应用,利用李群理论分析方法计算偏微分方程的对称相对来说是一种普遍的工具[2-5],近几年来李群分析方法早已应用到新的非线性科学领域——偏微分-积分方程中[6-8].本文利用李群方法[4-5]研究位势Burgers方程,寻找该方程所接受的单参数伸缩变换群,从而找到其对应的对称,最后给出其对应的自相似解.
2 位势Burgers方程(2)的自相似解

的不变条件要求

故位势Burgers方程(2)具有对称
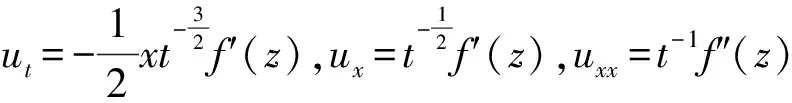
令y=f′(z),于是该方程变成Bernoulli方程

其通解为

从而位势Burgers方程(2)的自相似解为
3 位势Burgers方程(2)的行波解
设u=U(ξ),ξ=x-at是方程(2)的解,则方程(2)转化为一常微分方程
(3)


4 结论
本文是李群理论分析方法中的伸缩变换群在非线性二阶偏微分方程——位势Burgers方程(2)中应用的一个例子,仍可看作对文献[9]的一种补充和延续.应用与文献[8-9]类似的方法找到了位势Burgers方程(2)所接受的伸缩变换群,然后利用位势Burgers方程(2)所具有的对称找到了该方程的自相似解,并使用函数变换法找到了位势Burgers方程(2)的显式解析行波解.
