考虑跃迁系数的轴向受力铁木辛科梁的自由振动

陈岳阳， 李翔宇

(西南交通大学 力学与工程学院， 四川 成都 610031)

0 引 言

目前，承受轴向力作用的梁广泛应用于土木工程，生物医学和机械制造等领域[1-3].由于轴向受力的梁具有优良的拉伸和弯曲性能，其力学行为，例如振动，屈服，弯曲等，一直受到科研人员的广泛关注[4-7].值得指出的是，在轴向受力铁木辛科梁的变形过程中，轴向力的作用方向在相关文献中有两种假设：第一种是假定轴向力与梁的中性轴相切[8-9]；另一种则认为轴向力垂直于变形后的梁的横截面[10-11].这两种假设导致轴向受力的铁木辛科梁的力学行为呈现不同的结果，即轴向受力铁木辛科梁的许多力学问题仍需要做进一步探讨.基于此，本研究着重分析了轴向受力铁木辛科梁的自由振动问题，同时系统地探究了轴向力的作用方向对该梁的影响.

1 统一模型和特征方程

1.1 统一模型

在笛卡尔坐标系Oxy下，考虑长度为L，高度为h的铁木辛科梁，其中包含着轴向力F(假设其在变形过程中保持不变)和一个外加的横向均布简谐载荷p(x,t)，具体如图1所示.

轴向载荷的作用方向对梁的力学行为非常重要，在文献中对此存在两种假设.这两种假设在欧拉梁模型中是一样的，但是对于铁木辛科梁来说，这两种假设会导致不一样的结果.对此，2016年，陈涛等[12]

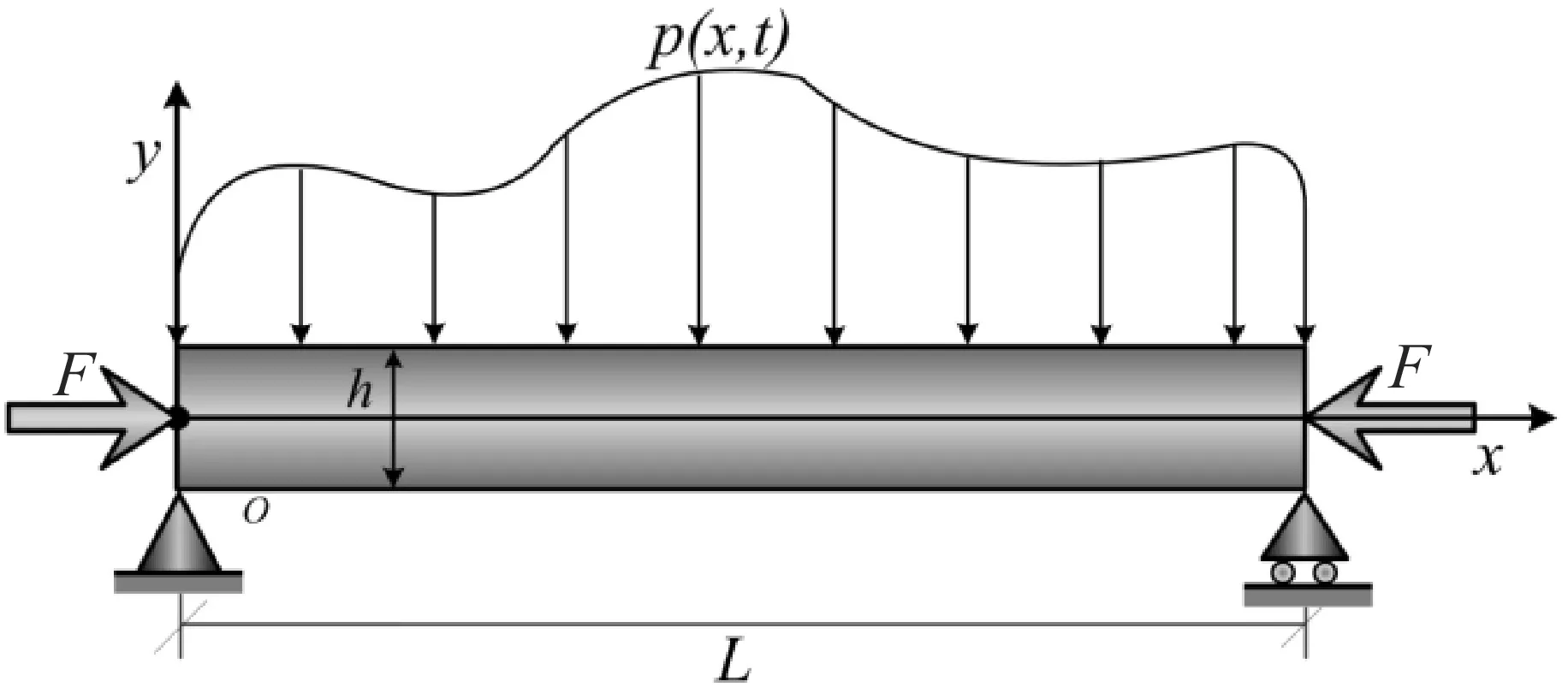
图1铁木辛科梁模型示意图

建立了一个统一的模型并引入一个跃迁系数(α)来表示轴向力的作用方向，α的取值范围为0到1，而上述两种假设能够由跃迁系数取特定值，即0或1，来实现.

在统一模型中，弯矩M和竖直方向的剪力V可表示为，

M=EIΨ′

(1)

V=κGA(Ψ-w′)+F[w′+α(Ψ-w′)]

(2)

根据牛顿第二定律，可得到如下的控制方程，

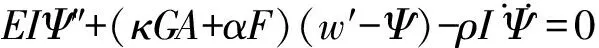
(3)

(4)

式中，κ，I，ψ，w，E，G，F，A和α分别代表着剪切修正因子、惯性矩、扭转角、挠度、剪切模量、杨氏模量、轴向力、截面面积和跃迁系数，式中的“·”和“′”分别

表示对时间t和空间坐标x的导数.

在研究中，假定一个压缩(或拉伸)轴向力为正(或负)，通过改变相应的系数，式(3)和式(4)可以退化成欧拉梁或瑞利梁的相应运动方程.

消去式(3)及(4)中的转角ψ，铁木辛科梁控制方程可以转化为位移表示的偏微分方程，

(5)

式中，

c1=κGA+αF-F,c2=κGA+αF.

在本研究中，只分析铁木辛科梁的自由振动，故假设，

w(x,t)=W(x)eiΩt

(6)

式中，W表示横向振动的振幅，Ω表示为系统的圆频率.

将式(6)带入式(5)中可得，

W″″+λ1W″+λ2W=0

(7)

式中，λ1=a1+a2Ω2,λ2=a4Ω4-a3Ω2.

事实上，欧拉梁和瑞利梁的自由振动微分方程和铁木辛科梁的方程(7)相同，仅除了欧拉梁和瑞利梁的微分方程中参数的表示不同.表1中给出了其对应参数的表达式.

表1 欧拉梁和瑞利梁的参数形式

对应于欧拉梁和瑞利梁，跃迁系数α不包含λi(i=1，2)的表达式，这是因为欧拉梁和瑞利梁的横截面在变形过程中的正方向假定为与挠曲线切线平行.

1.2 频率方程

从文献[4]可知，式(7)依赖于截止频率，

式(7)的通解可以表达成以下形式，

W(x)=A1coshs1x+A2sinhs1x+A3coss2x+

A4sins2x,Ω<Ωc

(8)

式中，

为方程的特征根.此外，Ai(i=1，2，3，4)为待定常数.

在文献[4]中详细阐述了截止频率的物理意义，本研究的分析将限制在Ω<Ωc的情况下.

为了确定固有频率，需要确定铁木辛科梁的边界条件.由于跃迁系数的引入，边界条件与相关文献相比将呈现不同的形式，其中系数α设置为1或0.表2为边界条件.

表2 边界条件

其中，

由通解和表2的边界条件，易得铁木辛科梁的频率方程如表3所示.

表3 频率方程

其中，

2 数值分析

2.1 有效性验证

考虑一个正方形截面(b=h=0.1 m)的铁木辛科梁，其长度L=0.5 m，密度ρ=2 778 kg/m3，杨氏模量E=7×1010N/m2，剪切模量G=2.61×1010N/m2.本研究利用此梁建立有限元模型来验证本研究方法的准确性，同时考虑采用多种边界条件来验证本研究的解析结果.为此，采用了正方形截面的简支梁、简支—滑动梁和固支梁，使用有限元软件ANSYS进行数值模拟，其中单元为beam 189，并将梁划分为201个节点.

引入Ncr和Ω0作为无量纲化的参考量.其中，Ncr表示不同边界条件的临界屈曲载荷.Ω0是无轴力时正方形截面(b=h=0.1 m)的简支铁木辛科梁的基频[9].

1)无轴力时，无量纲频率的对比情况如图2所示.

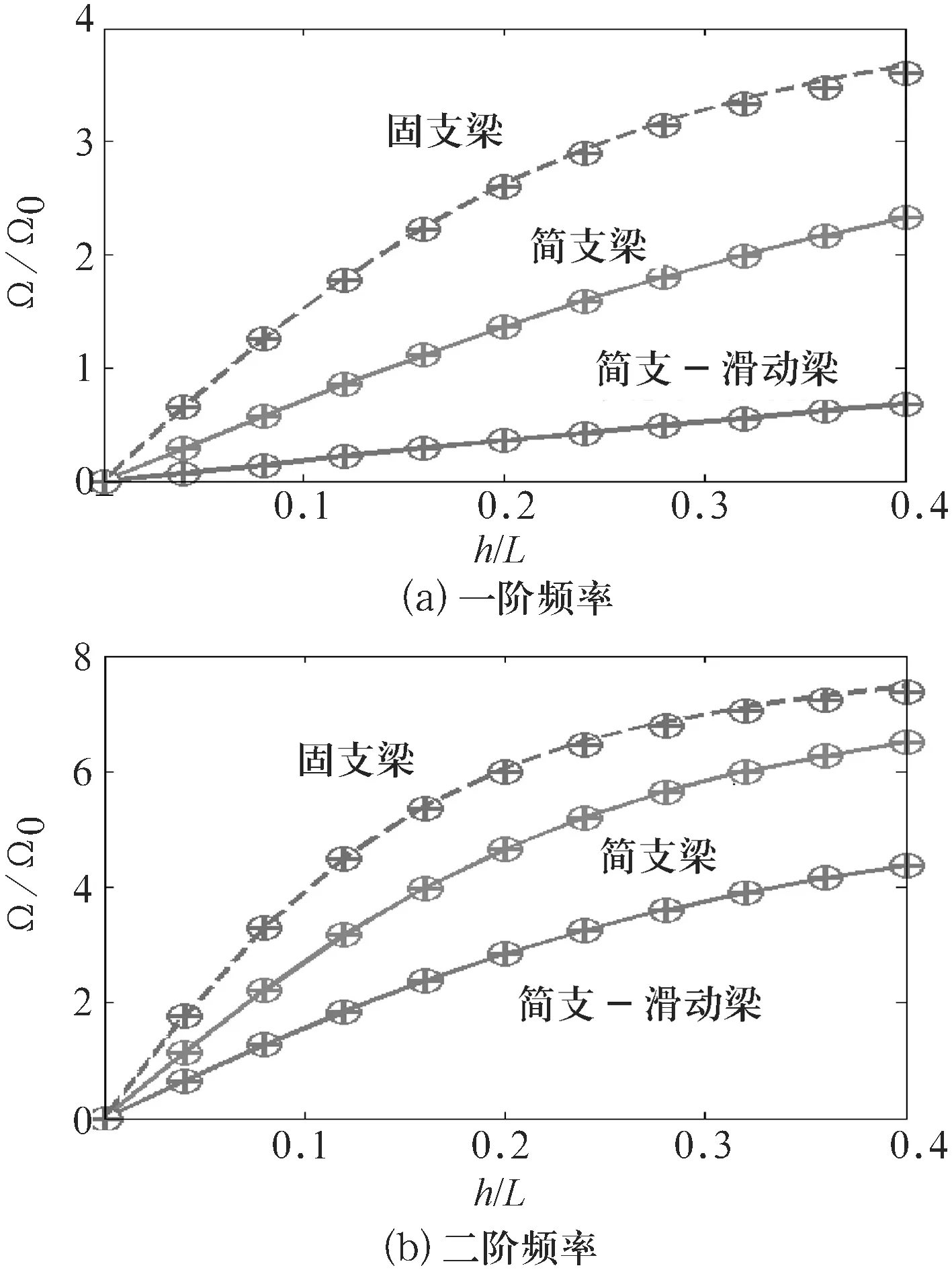
图2无轴力时无量纲频率的对比

由图2可知，简支梁、简支—滑动梁和固支梁不考虑轴向力时，前两阶模态的无量纲频率Ω/Ω0随高跨比h/L的变化结果(标识)与参考文献[9](实线)和数值模拟得到的结果(虚线)一致.值得注意的是，由于此时轴向力不存在，跃迁系数α对固有频率没有影响.

2)考虑轴力时，无量纲频率的对比情况如图3所示.

在图3中考虑了轴力的影响，无量纲频率随着轴向力的大小变化而变化，明显得出α=0对应的本研究结果与文献[9]给出的解以及有限元模拟值是一致的.这是因为文献和ANSYS软件都是假设梁处于变形过程中，轴向力的作用方向与变形层中性轴相切(即，α=0的情况)，当轴向力接近于临界屈曲力时，基频趋近于0.

2.2 轴向力对自由振动的影响

无量纲频率随无量纲轴向力的变化(h/L=0.3)如图4所示.

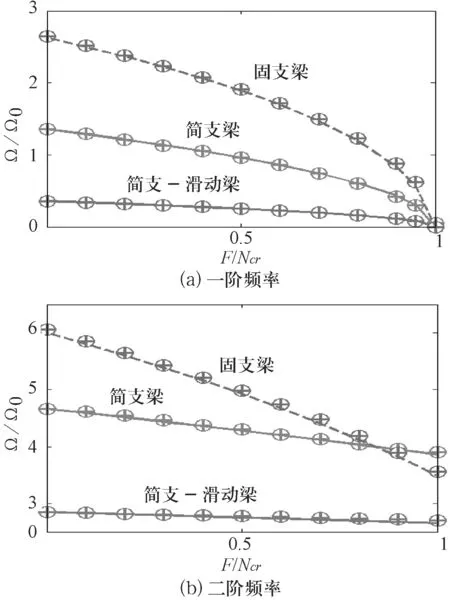
图3考虑轴力时无量纲频率的对比

图4无量纲频率随无量纲轴向力的变化(h/L=0.3)

由图4可知，给定高跨比h/L为0.3的梁，其固有频率在轴向载荷作用初期，频率降低得较慢，随着轴向载荷的增加，基频的衰减量逐渐变大，最后当轴向力达到临界屈曲力时，基频衰减到0.

图4中阴影区域表示α=0和α=1之间的频率差距.为了直观地分析跃迁系数的影响，定义相对误差RD=(Ωα=0-Ωα=1)/Ωα=0×100%.可以看出，跃迁系数α对固支梁的影响比简支梁大得多，这是因为轴向力在变形时对固支梁的剪力贡献比对简支梁的剪力贡献大.

2.3 高跨比对自由振动影响

无量纲高跨比的变化对无量纲频率的影响如图5所示.

由图5可知，考虑轴力F=0.8Ncr的固支铁木辛科梁的跃迁系数对自由振动的影响和高跨比h/L成正比，且跃迁系数对固支梁的影响较大.在较为极端的情况下(h/L=0.4)，固支梁的相对误差RD=49.49%，即跃迁系数对固支铁木辛科梁的影响非常显著.

图5无量纲频率随无量纲高跨比的变化

3 结 论

本研究利用包含跃迁系数的统一模型推导了多种边界条件下轴向受力铁木辛科梁的频率方程，利用数值模拟验证了结果的正确性.通过对比跃迁系数取0和1的情况发现，在考虑轴向力作用方向时，在较大的轴向力和高跨比的取值的情况下，跃迁系数对梁的自由振动的影响更显著.在数值模拟中，本研究发现跃迁系数对固支梁的自由振动有显著的影响，而对简支梁的影响较弱.在F=0.8 Ncr，h/L=0.4时，两种经典轴力方向对应的固支铁木辛科梁的相对误差可达到49.49%.