分数阶边值问题的区间估计

张艳辉，顾海波＊，孙 瑜，王仁正

（1.新疆师范大学 数学科学学院，新疆 乌鲁木齐 830017;2.新疆巴楚县第二中学，新疆 喀什 843800）

分数阶微积分学是经典的微积分学之一，它在机械工程、土木建筑工程、热能系统和力学中都扮演着重要的角色。此外，在其他学科方面应用也很广泛，比如光学、材料学、信号处理、辨识系统、控制论等。近年来，分数阶微分方程解的存在性方面也产生了一些研究成果［1-3］。另外，也有一些人研究了非线性分数阶微分方程边值问题正解的存在性［4-7］。

2010年W.G.Kelley和A.C.Peterson［8］得到了方程

存在唯一解，并且对解的存在区间进行了估计，区间长度需满足

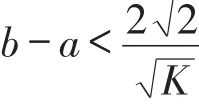
2016年R.A.C.Ferreira［9］讨论了两点Riemann-Liouville型分数阶微分方程

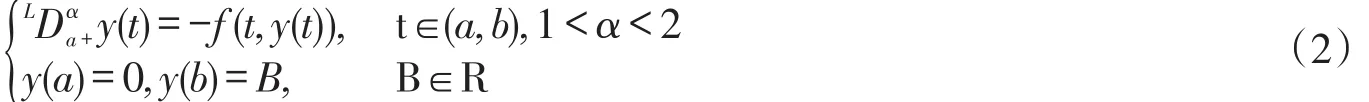
其解唯一存在的条件是

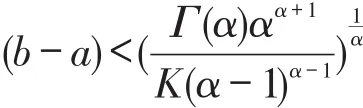
2017年B.Ahmad［10］研究了当 (a,b)满足

时，两点Liouville-Caputo型分数阶微分方程

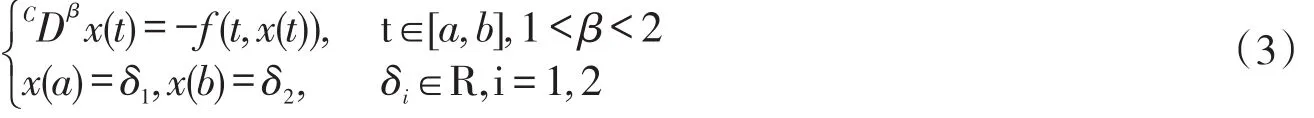
受以上研究结果的启示，文章讨论以下分数阶微分方程边值问题：

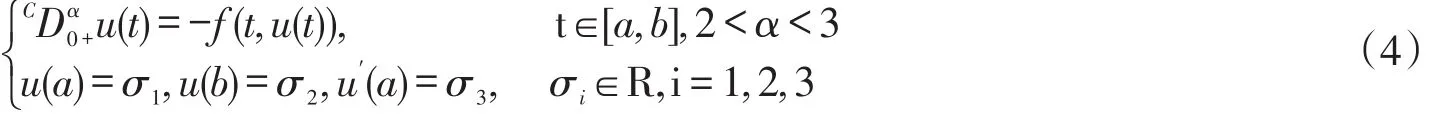
解的存在唯一性。这里CDα是Caputo型分数阶导数，它的定义将会在下一节给出，f是连续函数。文章将给出方程（4）的解的唯一存在的充分条件，并对解的存在区间加以估计。

1 预备知识

定义1.1［4］函数 f的分数阶积分公式为：

其中α＞0，右端积分在[a,∞)上逐点有定义，Γ(·)是Gamma函数。

定义1.2［4］函数 f的分数阶导数公式为：

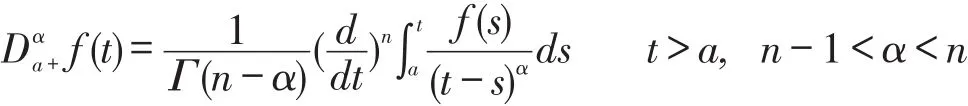
定义1.3［4］如果 f∈Cn[a,∞)，那么Caputo型分数阶导数为：

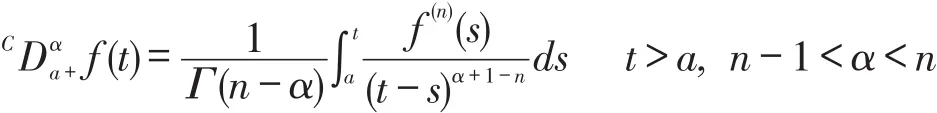
2 主要结果

在这一部分，将利用Banach不动点定理证明方程（4）解的存在唯一性。首先，给出一个Banach空间P，P=C([a,b],R)，它包含了所有的[a,b]→R上的连续函数；其次，定义了x的范数为

引理2.1 函数u∈C2[a,b]是方程（4）的一个解，当且仅当

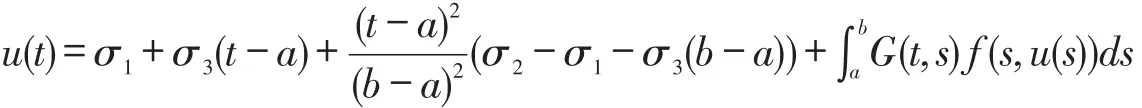
这里G(t,s)是Green's函数，形式如下：

证明 分数阶微分方程（4）的解与以下积分方程是等价的：

这里c1,c2,c3是任意的常数，由边界条件可以得到 c1=σ1,c2=σ3。

另外，u(b)=σ2意味着

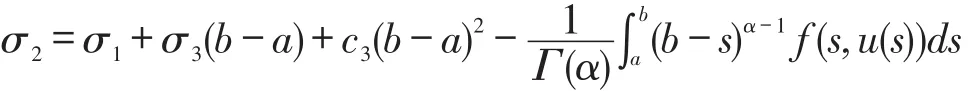
通过计算，有

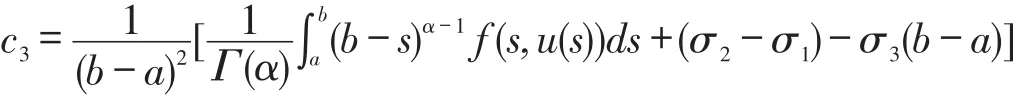
把 c1,c2,c3代入（6）式中，有

命题2.2 令G为引理2.1中所描述的，那么

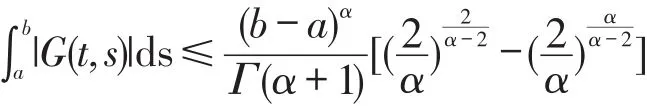
证明

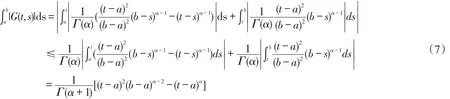
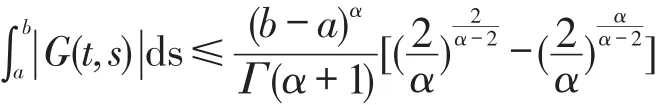
定理2.3 如果 f:[a,b]×R→R是一个连续函数，并且它满足Lipschitz条件：

那么，方程（4）有唯一解的充分条件是：

证明 由引理2.1，定义一个算子T，T:P→P，

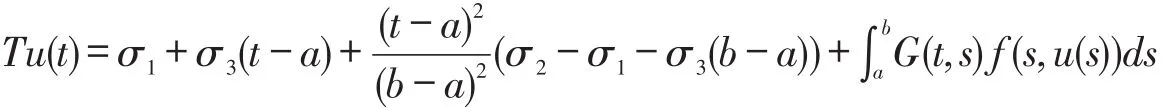
这里G是由（5）式所给出的，要说明Tu=u，也就是说，算子T有唯一的不动点，这就暗含着方程（4）只存在唯一的解。

令u,v∈P ，那么

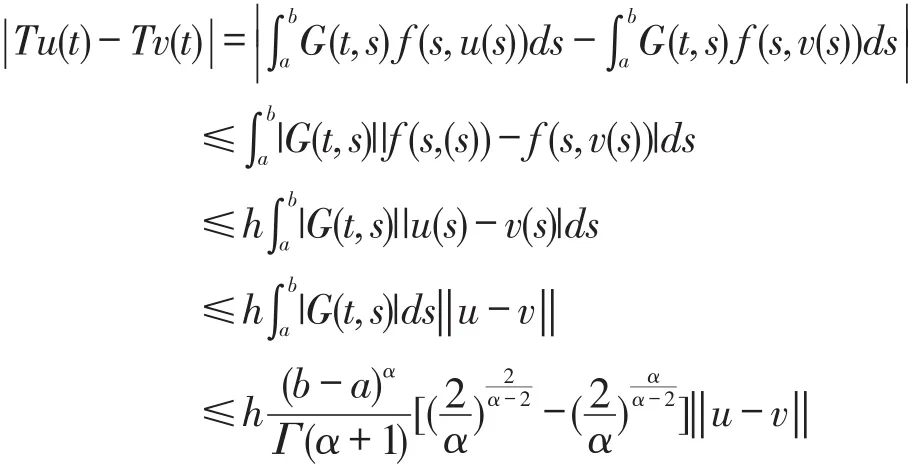
由命题2.2和Banach不动点定理，得到了方程（4）在[a,b]存在唯一解。

注：定理2.3说明方程（4）在[a,b]存在唯一解，并且说明了解的存在区间需要满足的条件。