桥梁钢裂纹尖端张开位移与试样厚度关系式的改进
2019-01-02,
,
(武汉理工大学交通学院,武汉 430063)
0 引 言
随着材料科学的发展与冶炼技术的提高,现有建筑钢材不仅种类繁多,而且力学性能也相差较大。在建造钢结构建筑物时,焊接是结构件常用的一种连接方式。焊接接头易萌生裂纹,在服役过程中,微裂纹在外载荷的作用下不断扩展,并逐步演化成肉眼可见的大裂纹,最终导致结构件的失效。国外有关重要钢结构建筑的规范规定:在设计阶段,必须测试相应焊接工艺下接头的断裂韧度;只有当焊接接头的断裂韧度达到规范给出的允许值时,才允许进行施工。断裂韧度表征的是材料抵抗裂纹扩展的能力,包括应力强度因子KC、能量释放率G、裂纹尖端张开位移(CTOD)和J积分等4种参量。其中,CTOD的测试技术成熟、原理简单,是常用的断裂韧度指标[1]。在测试CTOD时,常采用标准矩形截面的三点弯曲试样。在相同的试验温度下,同种材料不同厚度试样测得的断裂韧度是不同的:CTOD值随试样厚度的增加呈现出先增后降,最后稳定于常数的变化趋势[2-5]。这种现象即为厚度效应,反映出试样厚度对断裂韧度的影响。
在CTOD与试样厚度的关系方面已有相关研究。2013年,闫鹏帅等[6]首次提出了CTOD值δ与试样厚度t的关系式(厚度效应关系式)。然而,在用该关系式拟合不同厚度桥梁钢试样的CTOD值时,发现拟合值与试验数据间的误差较大,最大相对误差达到了15.6%,因此有必要对该厚度效应关系式进行改进。
作者介绍了闫鹏帅等所得厚度效应关系式的具体推导过程,分析了其拟合值误差较大的原因,并对其进行了改进;使用不同厚度桥梁钢试样的CTOD试验数据对改进后的厚度效应关系式进行了验证。
1 厚度效应关系式
1.1 原关系式的推导
根据Griffith表面能理论,对于含中心穿透裂纹的无限大板,裂纹扩展时G与表面能S存在如下关系[7]:
G=2S
(1)
对于Ⅰ型裂纹,G与KC的关系为
(2)
式中:E′为广义弹性模量。
当试样厚度较小时,试样处于平面应力状态,E′=E(E为弹性模量);当试样厚度较大时,试样处于平面应变状态,E′=1/(1-ν2)(ν为泊松比)。
将式(2)代入式(1),得到
(3)
根据Barenblatt吸附力理论与Dugdale带状屈服模型,在平面应力状态下,式(3)可变换成如下形式[8]:
(4)
式中:σ为裂尖垂直于裂纹扩展面的应力;ε为裂尖塑性区正应变;ε′为正应变极限值。

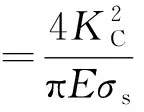
(5)
式中:σs为屈服强度。
联立式(4)和式(5)可知,当t趋近于0且试样处于平面应力状态时,δ与t成正比。当t很大时,由试验结果可知,δ会稳定于常数δm(即平面应变下的CTOD值)。以这两点为基础,闫鹏帅等应用构造法提出了δ与t的关系式,如下:
δ=ξtexp(-kth)+δm[1-exp(-kth)]
(6)
式中:ξ,k为材料参数;h为厚度t的幂,其功能是调节曲线形状。
式(6)由两部分构成:第一部分即ξtexp(-kth),代表的是平面应力区域对断裂韧度的贡献;第二部分即δm[1-exp(-kth)],代表的是平面应变区域的贡献。当t从0逐步增大时:第一部分中的exp(-kth)将从1减小至0,表明平面应力对断裂韧度的贡献逐渐减小;第二部分中的1-exp(-kth)将从0增大至1,表明平面应变对断裂韧度的贡献逐渐增大。
1.2 原关系式存在的问题及改进
闫鹏帅等[6]在用式(6)拟合桥梁钢的CTOD试验值时,效果不甚理想,最大相对误差达15.6%。作者认为这一问题出在式(6)所用的函数形式上。令ξ=0.35,k=0.15,δm=0.5 mm,h=1,则式(6)的函数曲线见图1。
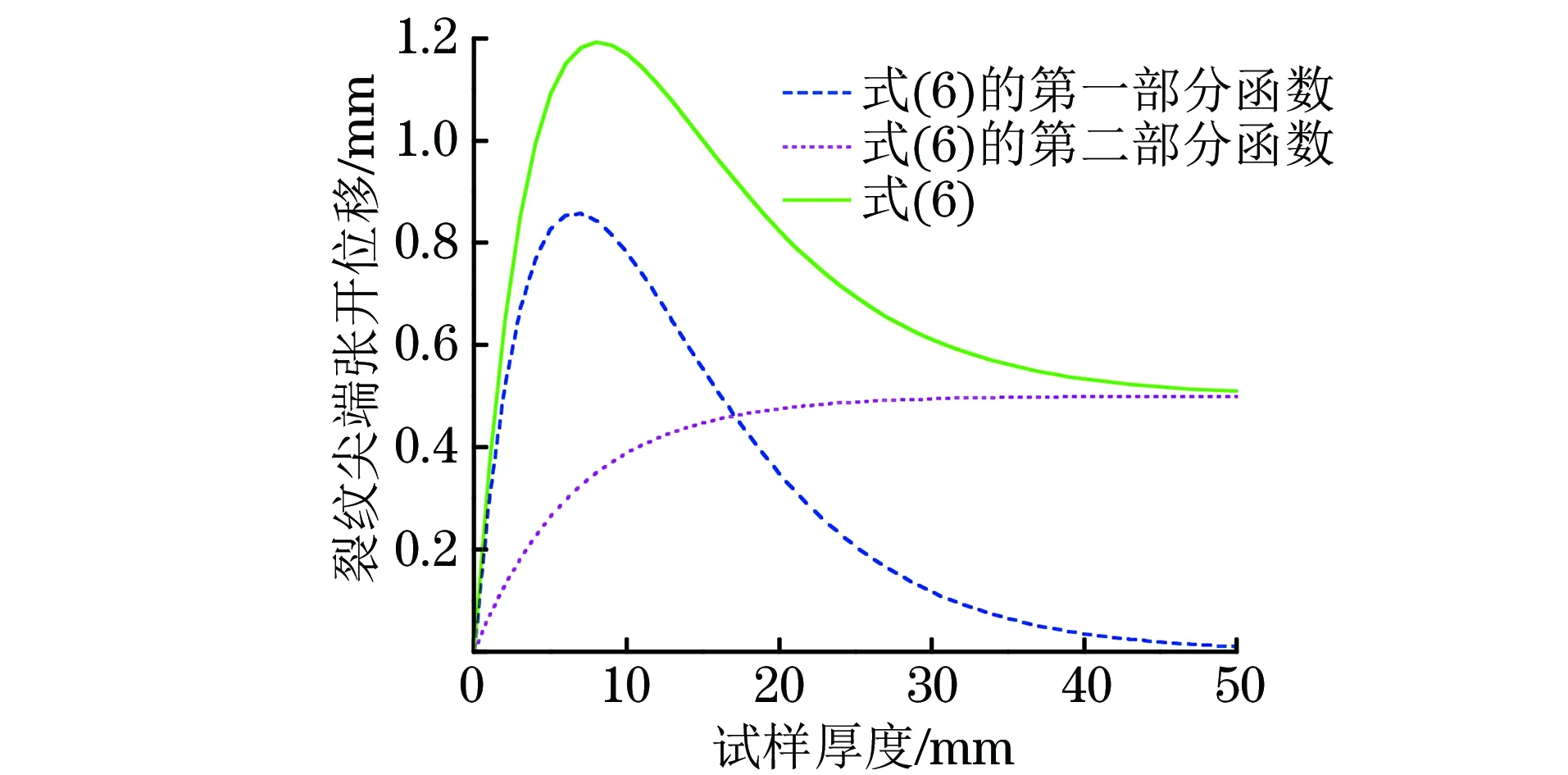
图1 式(6)的函数曲线Fig.1 Function curves of Eq.(6)
由图1可以看出,式(6)的函数曲线与断裂韧度随试样厚度变化的趋势是一致的。然而由文献[10]中不同厚度3种桥梁钢的CTOD试验结果可知:当试样厚度为30 mm左右时,CTOD值最大;当试样厚度达到50 mm左右时,CTOD值渐渐趋于常数。通过调节式(6)中的参数大小,使其拟合曲线与桥梁钢的CTOD试验结果相重合。式(6)的第二部分只需将δm调整至桥梁钢在平面应变下的CTOD值即可;而在对第一部分的参数进行调整时,当将峰值位置向右调整到t为30 mm处时,函数曲线会变得“矮胖”,在t为30~50 mm间,CTOD值不可能陡降到0。因此,式(6)第一部分的函数形式不合理。
要改进式(6),就需要找到“山峰”形曲线的函数,并且该函数在波峰的右边能迅速减小至0。由此,作者联想到了极值分布的概率密度函数,因为该函数曲线正好满足上述要求。用概率密度函数替换式(6)的第一部分函数,得到的厚度效应改进关系式为
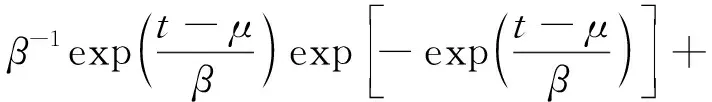
δm1-exp-kt
(7)
式中:μ,β为材料参数。
在Matlab软件平台上对曲线进行拟合,为了避免由于参数初始值设置不当而得到局部最优解,分成两个步骤进行拟合。第一步,试参数。编程描出试验数据点,在同一幅二维图像中,绘制出式(7)的函数曲线;手动调节式(7)中的参数,使曲线尽可能靠近数据点,但无需穿过数据点;当曲线离数据点比较近时,记录下此时曲线的参数,作为下一步拟合时的初始参数值。第二步,曲线拟合。利用软件自带的曲线拟合函数lsqcurvefit,将上一步记录的拟合初始参数值代入该函数中,随后程序自动按最小二乘法计算出最合适的参数值。按照这两个步骤,便可得到全局最优解。
2 试验验证
用文献[10]中室温下14MnNbq钢、14MnNbq钢接头焊缝和16Mnq钢的CTOD试验值对式(7)进行验证。
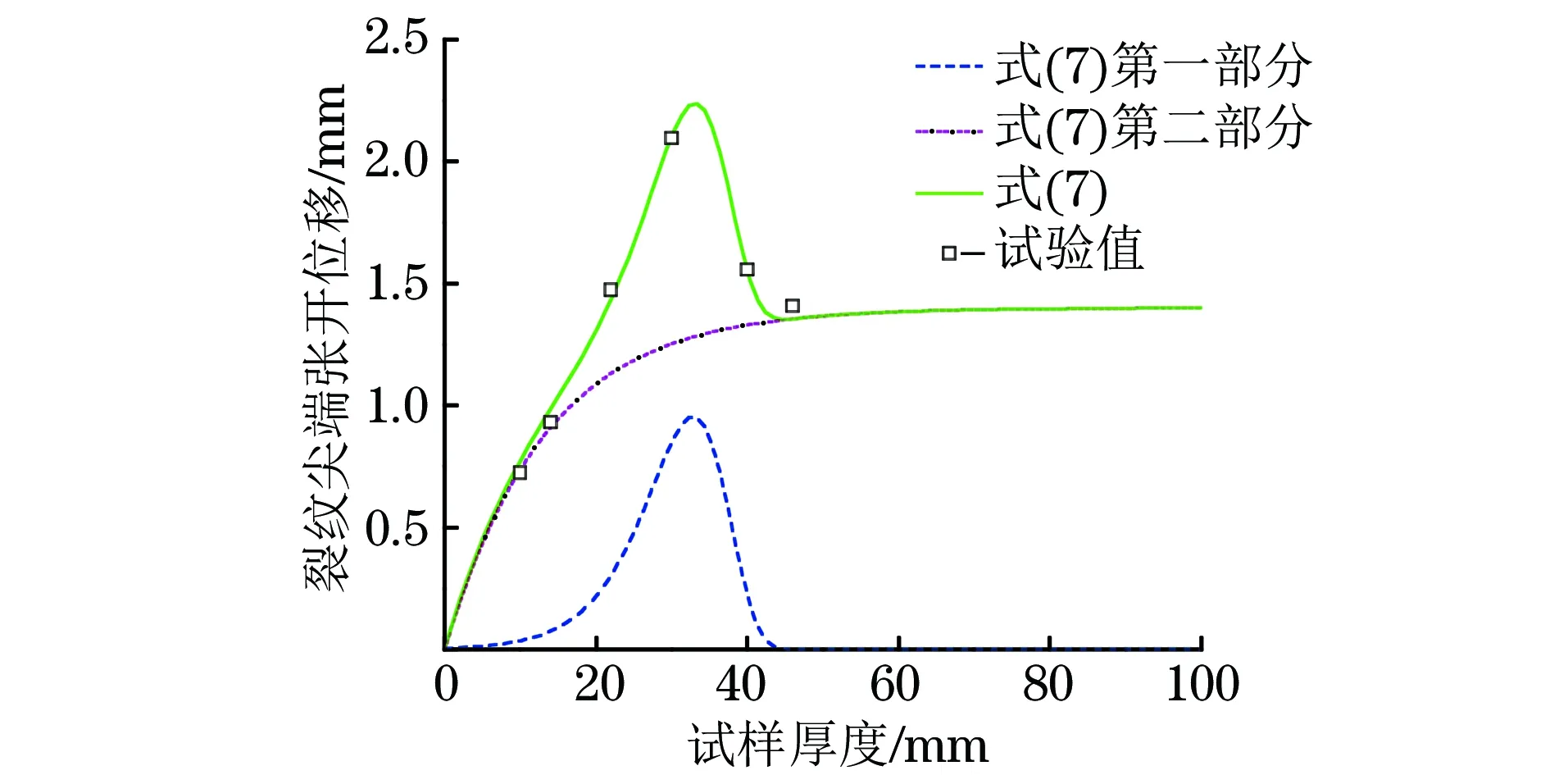
图2 14MnNbq钢CTOD试验值及其拟合曲线Fig.2 CTOD test values and the fitting curves for 14MnNbq steel
2.1 对14MnNbq钢的适用性
按照前文所说的拟合步骤,对14MnNbq钢的CTOD试验值进行拟合,拟合曲线见图2,拟合关系式为

1.4[1-exp-0.075t]
(8)
利用式(8)计算得到的δ及其与试验值的相对误差见表1。
表1不同厚度14MnNbq钢CTOD的试验值和式(8)
计算值及其相对误差
Table1CTODtestvaluesandcalculationvaluesfromEq.(8)andtheirrelativeerrorsfor14MnNbqsteelwithdifferentthicknesses

t/mmδ/mm试验值计算值相对误差/%100.724 30.775 57.06140.931 50.986 25.87221.474 01.434 72.67302.094 82.102 40.36401.556 31.553 70.17461.408 21.355 83.72
由图2可以看出,由式(7)拟合得到的曲线能很好地反映14MnNbq钢CTOD试验值变化的规律。式(7)的第一部分对提高拟合结果准确性的贡献最大。由表1可以看出,由式(8)计算得到的CTOD值与试验数据的最大相对误差为7.06%,最小为0.17%。由此可见,作者提出的厚度效应关系式的改进方法是合理且有效的。
2.2 对14MnNbq钢接头焊缝的适用性
同理,按照前文所说的拟合步骤对14MnNbq钢接头焊缝的CTOD试验值进行拟合,拟合曲线见图3,拟合关系式为

0.151-exp-0.08t
(9)
利用式(9)计算得到的δ及其与试验值的相对误差见表2。
由图3和表2可以看出,改进后的厚度效应关系式对14MnNbq钢接头焊缝CTOD试验值的拟合准确性较高,最大相对误差为7.63%,最小为0.95%。由此可见,改进后的厚度效应关系式适用于14MnNbq钢接头焊缝。
表2不同厚度14MnNbq钢接头焊缝CTOD的试验值和
式(9)计算值及其相对误差
Table2CTODtestvaluesandcalculationbaluesfromEq.(9)andtheirrelativeerrorsforweldof14MnNbqsteeljointwithdifferentthicknesses

t/mmδ/mm试验值计算值相对误差/%100.268 80.279 64.01140.446 30.415 16.99220.771 70.792 22.65300.923 70.914 90.95400.188 90.203 07.49460.158 50.146 47.63
2.3 对16Mnq钢的适用性
按照前文所说的拟合步骤对16Mnq钢的CTOD试验值进行拟合,拟合曲线见图4,拟合关系式为

0.541-exp-0.21t
(10)
利用式(10)计算得到的δ及其与试验值的相对误差见表3。
从图4和表3可以看出,改进后的厚度效应关系式对16Mnq钢CTOD试验值的拟合准确性较高,最大相对误差为1.66%,最小为0.54%。由此可见,改进后的厚度效应关系式适用于16Mnq钢。
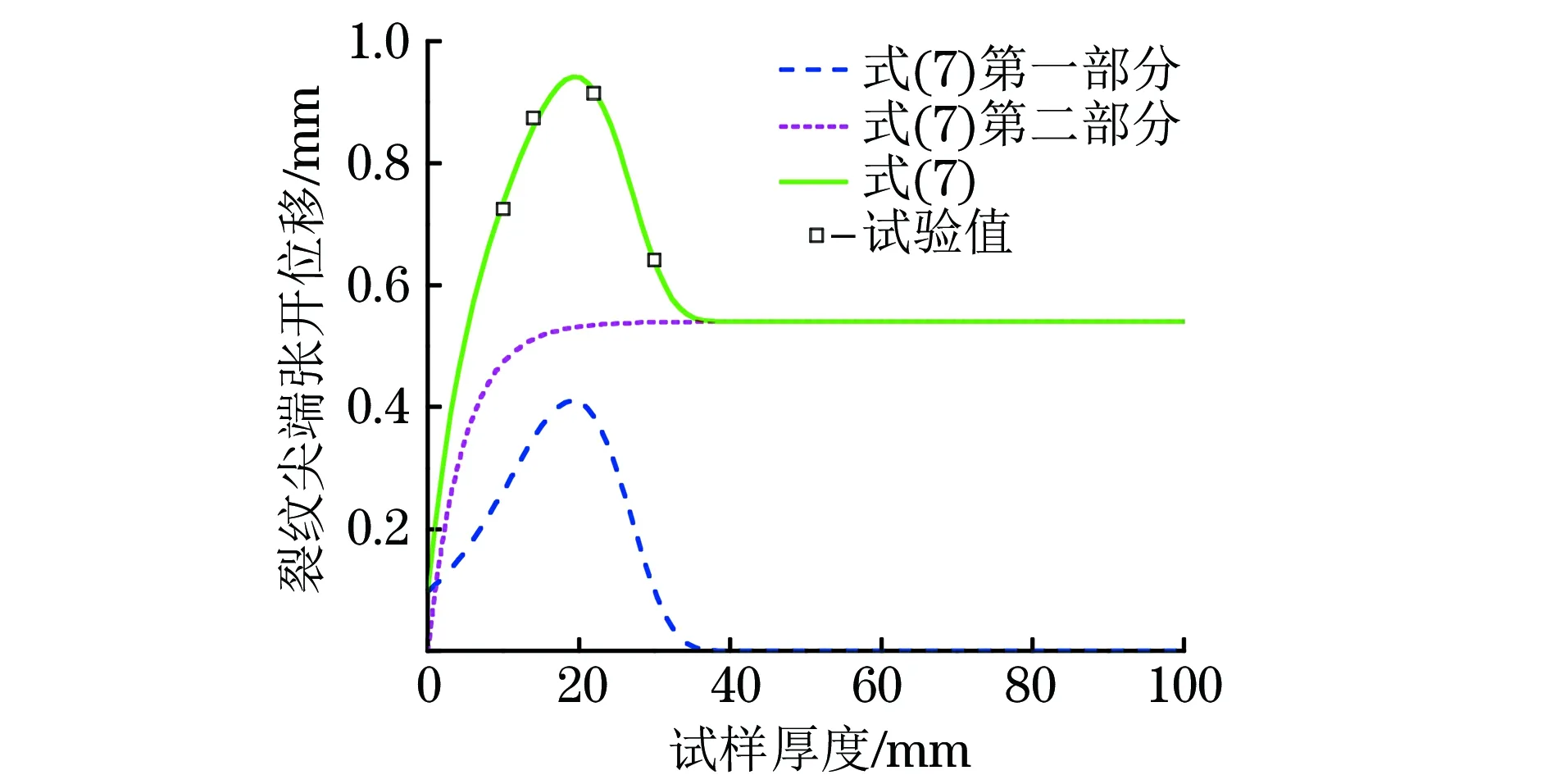
图4 16Mnq钢CTOD试验值及其拟合曲线Fig.4 CTOD test values and the fitting curves of 16Mnq steel
Table3CTODtestvaluesandcalculationvaluesfromEq.(10)andtheirrelativeerrorsfor16Mnqsteelwithdifferentthicknesses

t/mmδ/mm试验值计算值相对误差/%100.724 40.736 51.66140.874 00.860 21.58220.913 90.919 10.57300.640 70.637 20.54
综上所述,改进后的厚度效应关系式对3种桥梁钢试样CTOD试验值的拟合准确性均较高,该关系式对桥梁钢具有普适性。
建立厚度效应关系式的主要目的是为了进行断裂韧性的预测。对于某一材料,若已知其在若干厚度下的CTOD值,则可以采用改进的厚度效应关系式拟合已知的CTOD值,再使用拟合曲线预测其在其他厚度下的CTOD值,以此来表征断裂韧性。已知的数据点越多,预测的结果就越接近真实值。由于数据点对拟合曲线有约束作用,所以作者给出的厚度效应改进关系式具有适用的厚度范围,预测试样的厚度应在试验数据测试时所用试样的最小厚度和最大厚度之间。在该厚度范围外,由于缺少试验数据的支撑,虽然有拟合曲线经过,仍无法保证预测结果的准确性。
3 结 论
(1) 闫鹏帅等建立的厚度效应关系式的第一部分(即平面应力部分)函数形式不合理,导致对CTOD值的预测不准确;用概率密度函数替换第一部分函数,得到厚度效应改进关系式。
(2) 用不同厚度桥梁钢试样(14MnNbq钢、14MnNbq钢接头焊缝、16Mnq钢)的CTOD试验值对厚度效应改进关系式进行验证,拟合得到的CTOD值与试验值的相对误差较小,说明厚度效应关系式的改进方法是合理有效的,并且厚度效应改进关系式适用于不同的桥梁钢。
(3) 利用该厚度效应改进关系式进行断裂韧性预测时,预测试样的厚度应在试验数据测试时所用试样的最小厚度与最大厚度之间,这样才能保证预测结果的准确;在此厚度范围外,由于缺少试验数据的约束,不建议进行断裂韧度的预测。
