无油涡旋压缩机的动力特性与摩擦损失分析
2019-01-02郝红梅朱永军
彭 斌,郝红梅,朱永军
(兰州理工大学机电工程学院,甘肃 兰州 730050)
无油涡旋压缩机是第三代容积式压缩机,具有可靠性高、结构简单、噪声小、振动低、效率高的特点。无油涡旋压缩机对精度以及形位公差的要求极高,涡旋压缩机的动力特性对涡旋压缩机的性能影响十分大。涡旋压缩机的转子系统作为压缩机传输动力的枢纽,其各个零件在工作过程中会受到各种力与力矩的作用,这些零部件的动力特性过差将会大大降低涡旋压缩机的性能,因此对涡旋压缩机各零部件的动力特性的研究是无油涡旋压缩机动力特性研究中不可或缺的一部分[1]。
国内外许多学者已经对涡旋压缩机的动力特性做了许多研究,并且取得了相当不错的成果。Ishii等[2]通过对比说明了涡旋压缩机偏心振动的问题,得出了涡旋压缩机良好的动力特性;Morishita等[3]对动盘动态行为进行了推导与分析;Morris等[4]对涡旋压缩机的运动规律进行了分析;彭斌等[5]对变截面涡旋压缩机的几何模型及摩擦损失进行了研究;柏杰等[6]通过热力学关系对动盘、十字滑环进行了分析计算,并且通过高斯消去法得到了力与主轴转角的变化关系;吴建华等[7]对不同结构形式的动盘进行了分析,并以此为依据给出了整机的动力计算方法。
本文以排气量为0.6m3/min的无油涡旋压缩机样机为例,通过对涡旋压缩机主要运动部件小曲拐、动盘以及主轴的受力分析,建立了涡旋压缩机的动力学模型,并以此对主要摩擦部件进行了摩擦分析,所得到的结果将为涡旋压缩机的优化设计提供重要的参考。
1 小曲拐的受力分析
涡旋压缩机由于切向力的存在会使动静盘不能正常啮合,无油涡旋压缩机采用小曲拐防自转机构来限制此自转力矩。图1所示为小曲拐的受力图。按照小曲拐的运动方向建立动坐标系。图中所示:动盘作用于小曲拐的力为Qi,机架作用于小曲拐的力为Q,动盘作用于小曲拐的摩擦力为f1,机架作用于小曲拐的摩擦力为f2。

图1 小曲拐受力图
根据功能平衡关系可求得动盘对小曲拐的作用力Qi为[8]:
(1)
式中:Ft为动盘受到的切向力;ROr为偏心距;ROQ为动盘中心到小曲拐的距离;z为小曲拐的数目;i为小曲拐的数目基数;θ为主轴转角。
建立小曲拐力与力矩的平衡方程。
在R轴方向上,由∑FR=0得:
FC+Qi-Q+Fmsinθ=0
(2)
对Z轴取矩为0,由∑Mz=0得:
M1+f1(r1+e)+f2r2=0
(3)
对T轴取矩为0,由∑MT=0得:
(4)
式中:M2为小曲拐受到的力矩。
2 动盘的受力分析
涡旋盘是涡旋压缩机最重要的零件,也是压缩气体的零件。动盘的动力特性影响着动、静盘之间的啮合,决定着涡旋压缩机能否正常工作。
涡旋压缩机动盘受力如图2所示,同样按照涡旋压缩机运动的方向建立动坐标系,动盘主要受到的力和力矩如下:
1)动盘内气体压力产生的轴向力Fa、径向力Fr、切向力Ft。
2)动盘由于公转运动产生的离心力Fcs,其方向沿着动盘基圆中心与静盘基圆中心之间的连线,与径向力Fr方向相反:
Fcs=msROrω2
(5)
式中:ms为动盘质量。
3)曲柄销对动盘驱动力SR和ST及曲柄销产生的摩擦转矩MS:
(6)
式中:μ为接触面摩擦系数;RS为曲柄销的半径。
4)3个小曲拐对动盘的作用力分别为Q1,Q2,Q3,对动盘的摩擦力分别为fQ1,fQ2,fQ3,产生的摩擦转矩分别为MfQ1,MfQ2,MfQ3,对动盘轴向的作用力分别为FQ1,FQ2,FQ3。lQR1,lQR2,lQR3分别为3个小曲拐到R轴的距离,lQT1,lQT2,lQT3分别为3个小曲拐到T轴的距离。
MfQi=r1fQi
(7)
根据受力分析建立动盘的力和力矩的平衡方程。
在R轴方向上,有∑FR=0:
Fcs-Fr+Fmsr+SR+Q2-Q1-Q3=0
(8)
在T轴方向上,有∑FT=0:
Ft-Fmst-ST+fQ1-fQ2+fQ3=0
(9)
在Z轴方向上,有∑FZ=0:
Fa-FQ1-FQ2-FQ3=0
(10)
对R轴的力矩为0,即∑MR=0:
FtH/2-SThs+(fQ1+fQ3-fQ2)hQ-FQ1lQR1-FQ2lQR2+FQ3lQR3=0
(11)
对T轴的力矩为0,即∑MT=0:
Fcshc-SRhs-FrH/2+(Q1-Q2+Q3)hQ-FQ1lQT1-FQ2lQT2+FQ3lQT3-FaROr/2=0
(12)
对Z轴的力矩为0,即∑Mz=0:
MZ-MfQ1-MfQ2-MfQ3-MS-Q1ROQ-Q2ROQ-Q3ROQ=0
(13)
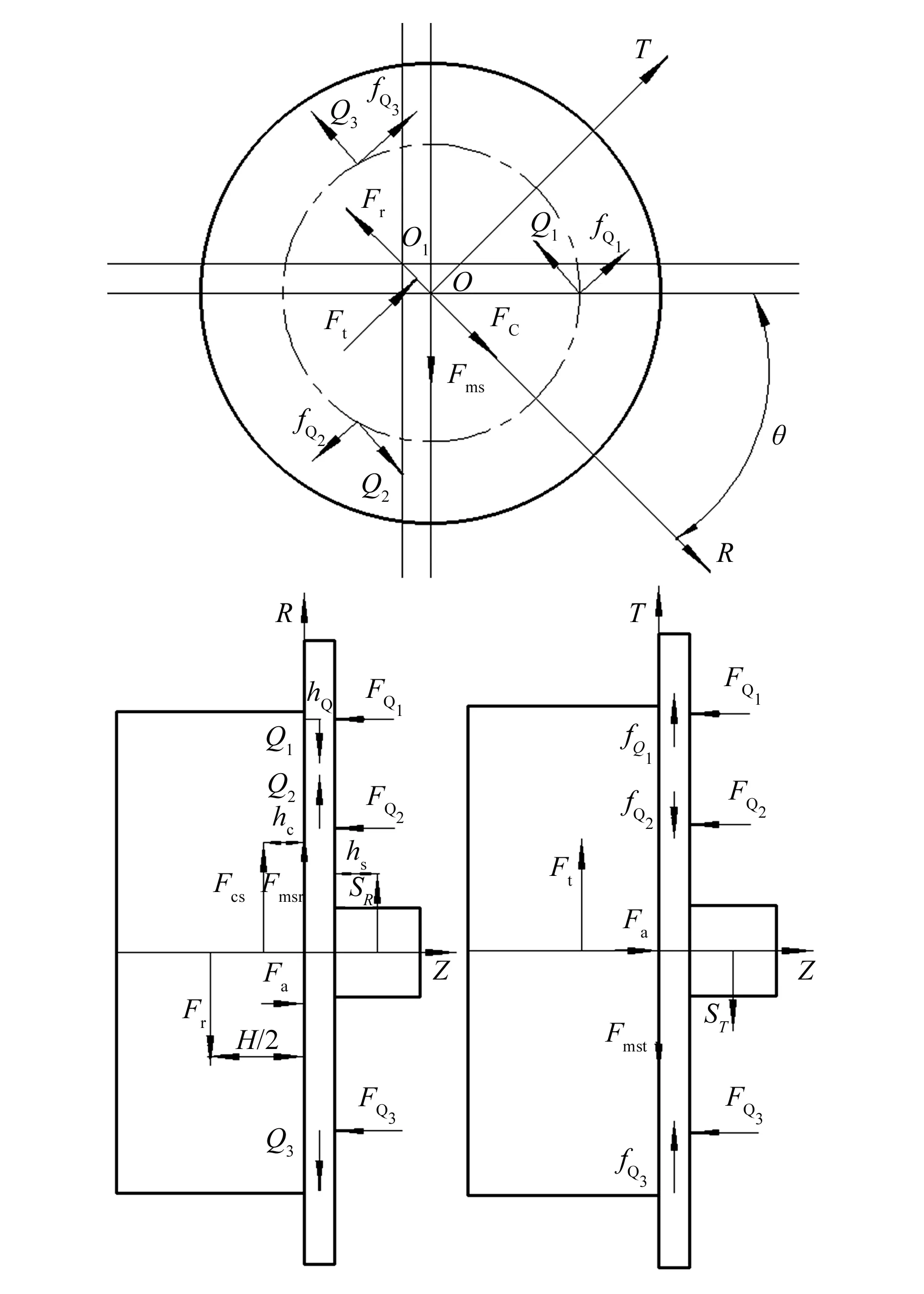
图2 动盘受力分析图
3 主轴受力分析
主轴是将电动机动力传输到动盘的零件,其动力特性的好坏将直接影响涡旋压缩机能否正常运转,因此对主轴的受力分析,将为解决因主轴变形引起的泄漏、摩擦等问题提供极其重要的依据。主轴的受力如图3所示,根据动盘运动来建立主轴的坐标系,主轴受到的力与力矩主要有:
1)动盘对曲柄销的作用力QR,QT及作用力产生的摩擦力矩MQ;
2)主轴承对主轴的作用力FZR,FZT及作用力产生的摩擦力矩MZ;
3)副轴承对主轴的作用力FFR,FFT及作用力产生的摩擦力矩MF;
4)大小平衡块产生的离心力Fcd,Fcx;
5)曲柄销产生的离心力Fcq;
6)电机的驱动力矩Md;
7)风轮产生的力矩Mf。
风轮产生的力矩Mf计算公式为:
(14)
式中:Sf为风轮扇叶总面积;ρ为气体密度;Rf为风轮中心到扇叶的距离;取空气阻力系数c=0.95[9]。
根据受力分析建立主轴的力和力矩的平衡方程。
在R轴方向上,有∑FR=0:
Fcq+QR-Fcd+FZR-FFR+Fcx=0
(15)
在T轴方向上,有∑FT=0:
QT-FZT+FFT=0
(16)
对R轴取矩为0,即∑MR=0:
QT(lz1+lz2)-FFTlz3=0
(17)
对T轴取矩为0,即∑MT=0:
(QR+Fcq)(lz1+lz2)-Fcdlz2+FFRlz3-Fcx(lz3+lz4)=0
(18)
对Z轴取矩为0,即∑MZ=0:
Md-MF-MF-MZ-MQ=0
(19)
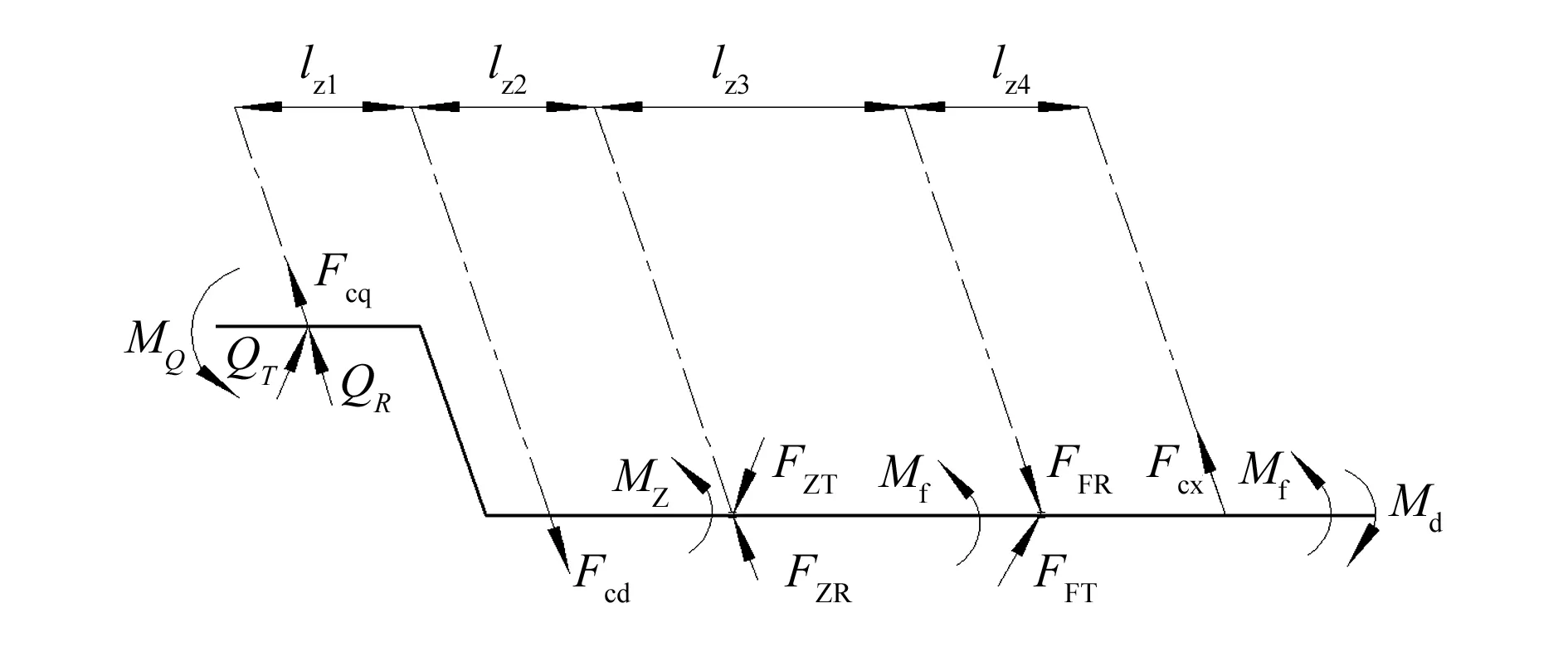
图3 主轴受力分析图
4 涡旋压缩机摩擦损失分析
4.1 小曲拐摩擦损失
小曲拐是防止涡旋压缩机发生自转的机构,小曲拐与动盘、机架之间会因为转动产生摩擦损失。小曲拐的摩擦损失功率Px为:

(20)
式中:Lx为小曲拐摩擦转矩;n为曲轴转速,其数值为1 440r/min;θ′为主轴转角的导数;T为主轴旋转一周的时间。
4.2 曲柄销摩擦损失
曲柄销的主要作用是将主轴的动力传输给动盘,使动盘公转平动。曲柄销与动盘之间会因为相对运动而产生摩擦力。曲柄销的摩擦损失功率Pcp为:

(21)
式中:Lcp为曲柄销摩擦转矩。
4.3 主轴承摩擦损失
由于涡旋压缩机特殊的偏心机构,使主轴承成为主轴的主要承力零件,主轴承由于主轴的高速旋转而产生摩擦损失。主轴承产生的机械摩擦损失功率PZ为:

(22)
式中:LZ为主轴承摩擦转矩。
4.4 副轴承摩擦损失
副轴承也是主轴上的承力零件,副轴承同样由于主轴的高速旋转产生摩擦损失。副轴承产生的机械摩擦损失功率PF为:

(23)
式中:LF为副轴承摩擦转矩。
4.5 机械效率计算
电机总输入功率除了很少一部分功率通过热量的方式散失之外,绝大部分都传送给了主轴。主轴的功率则通过驱动动盘运动传给动盘,一部分通过摩擦损失掉,还有一小部分通过泄漏、传热等方式散失。由于本文研究内容有限,此次主要研究摩擦产生的功率损失。
总的机械摩擦损失Pall为:
Pall=Px+Pcp+PZ+PF
(24)
主轴输入功Ps为:

(25)
式中:Ls为电机给主轴的输入转矩。
则涡旋压缩机机械效率η为:
(26)
5 求解结果与分析
利用MATLAB编程通过迭代方法求解式(1)~式(19)。
5.1 主轴受力分析
图4~图6分别为主轴承受力图、副轴承受力图、曲柄销受力图。由图中可以看出,在主轴旋转一周的过程中,起始部分与结尾部分受力是相同的,因此主轴承、副轴承、曲柄销的受力呈周期性变化,且主轴承的受力要大于其他受力。由图中看出这3个受力与切向力的趋势相同,这是由于在平面内,切向力要远远大于其他的作用力,因此曲柄销、主轴承与副轴承受切向力的影响最大。在θ=265°,即主轴转角值等于排气角值、切向力达到最大值之时,曲柄销、主轴承与副轴承受力同样达到最大值。
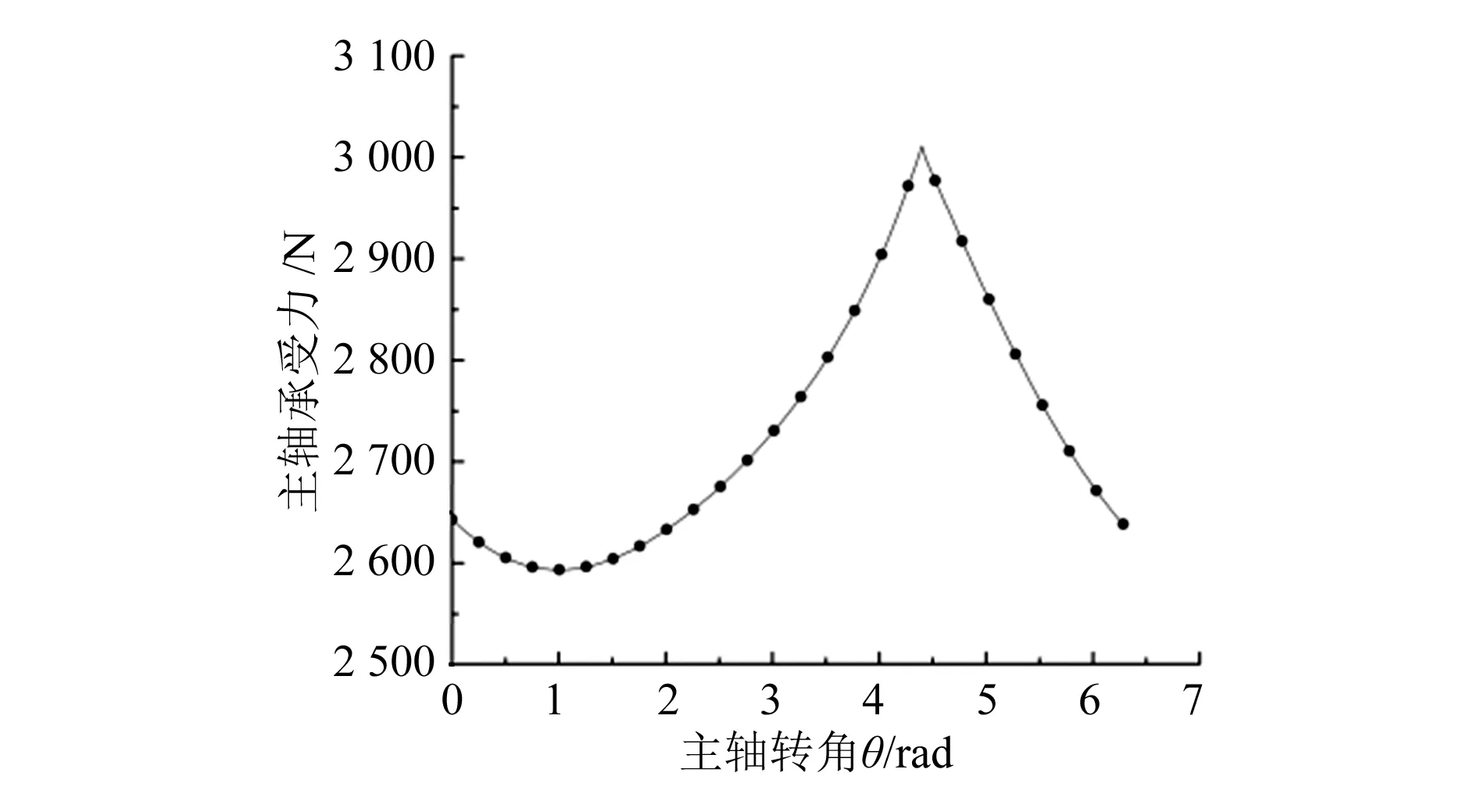
图4 主轴承受力

图5 副轴承受力

图6 曲柄销受力
5.2 主轴摩擦损失分析
图7~图9分别表示了曲柄销、主轴承与副轴承的摩擦损失,曲柄销、主轴承与副轴承的摩擦损失与受力的变化趋势类似。由图中看出,在主轴旋转一周的过程中,起始部分与结尾部分的摩擦损失相同,摩擦损失随着主轴转动呈周期性变化。切向力最大时摩擦损失达到最大值,主轴承的摩擦损失远远大于其他轴承,因此主轴承的摩擦损失是影响涡旋压缩机效率的最主要因素。
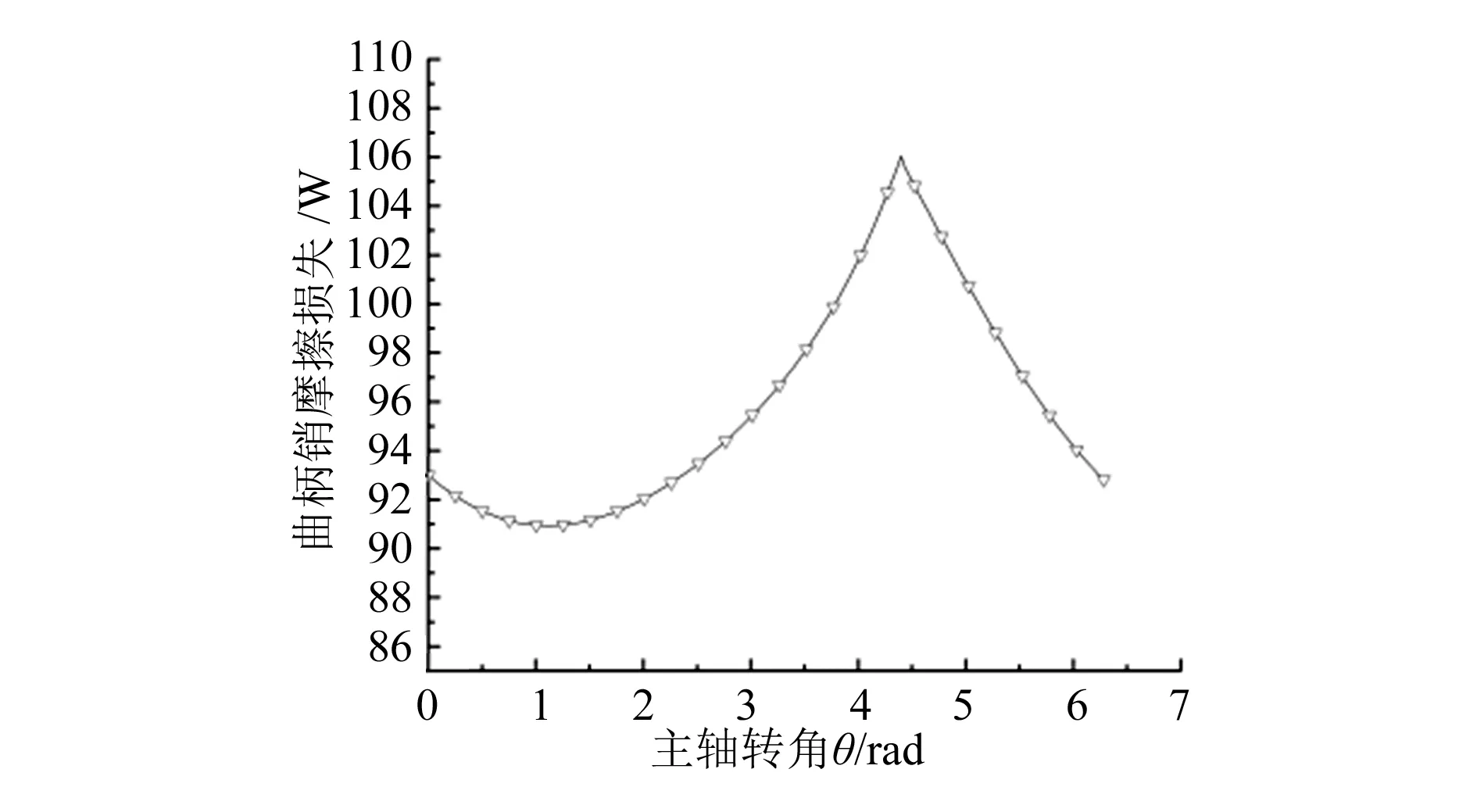
图7 曲柄销摩擦损失
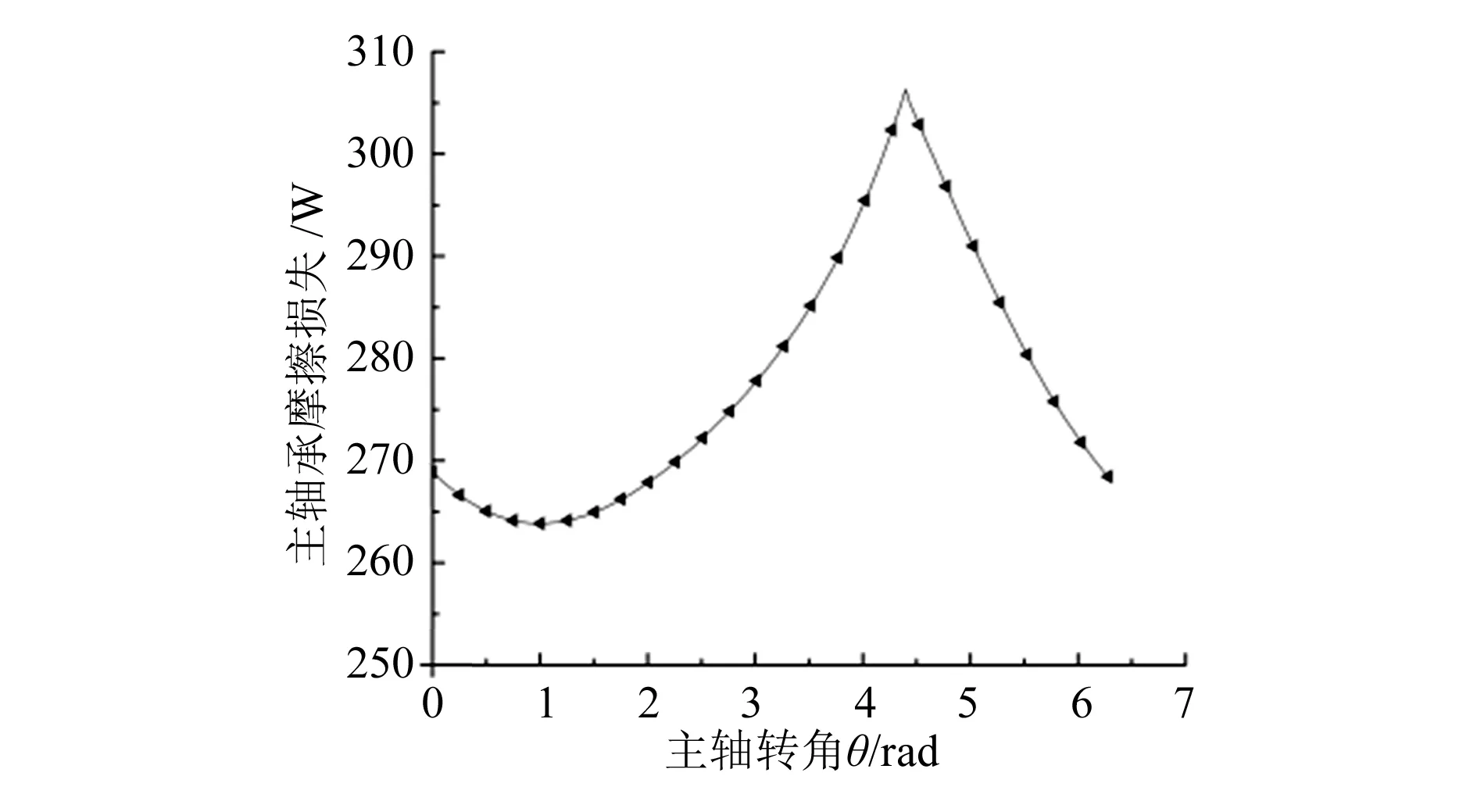
图8 主轴承摩擦损失
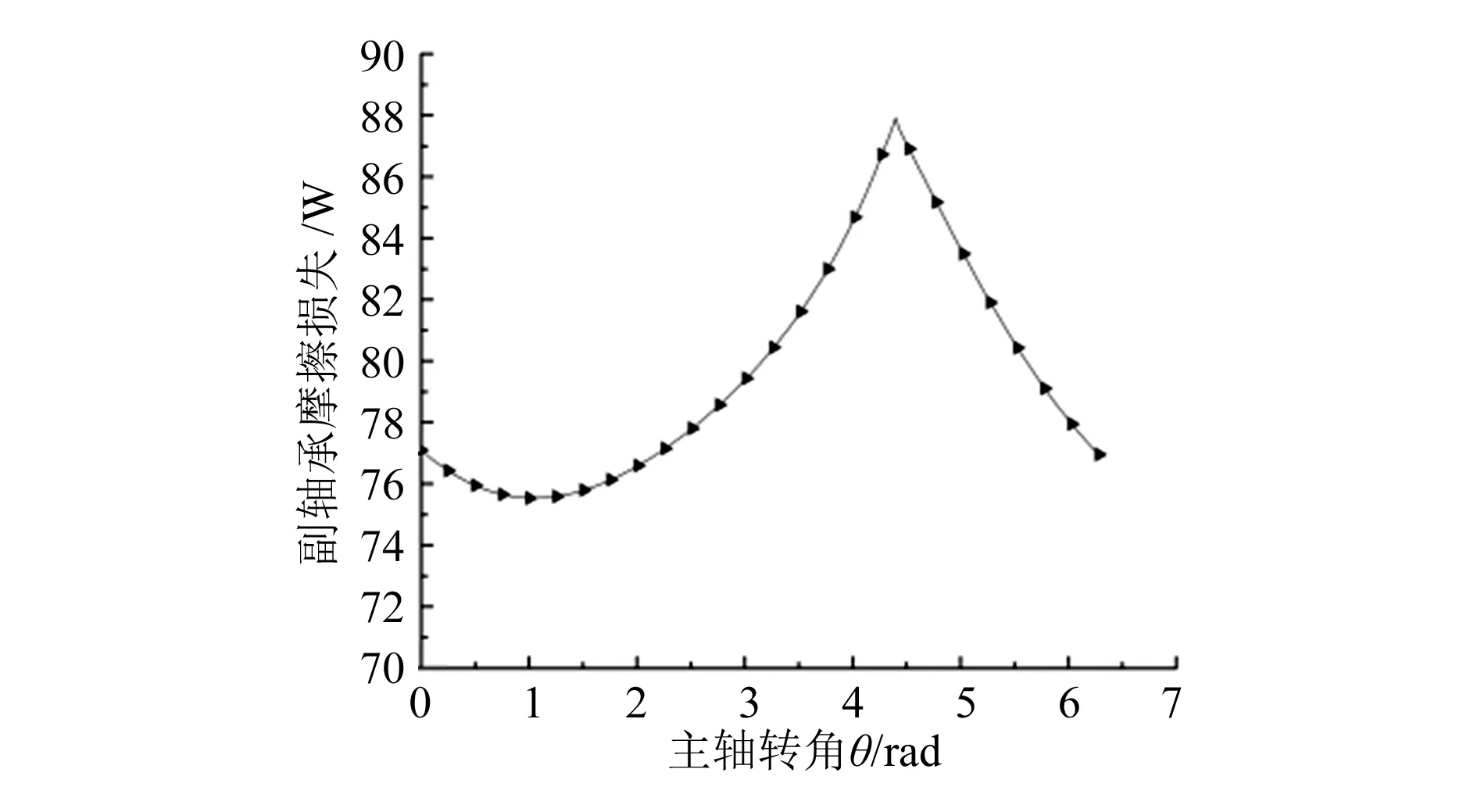
图9 副轴承摩擦损失
图10所示为涡旋压缩机的机械效率的变化图,由图中可以看出,气体进、出时刻的机械效率是相等的,因此涡旋压缩机的机械效率呈周期性变化。图中显示该涡旋压缩机的机械效率变化值约为0.027,由此可知,在主轴转动一周的过程中,整机的机械效率变化很小,说明此无油涡旋压缩机运行较平稳。
6 结束语
本文通过对无油涡旋压缩机主要零部件受力特性的分析研究,得出了无油涡旋压缩机在运行时振动幅度很小的结论,说明无油涡旋压缩机运行时具有很高的稳定性。

图10 机械效率
