随车起重机动臂油缸连杆优化及对比分析

2019-01-02畅思琦石联军

建筑机械 2018年12期

朱冰，畅思琦，石联军，任鹏

（山西航天清华装备有限责任公司，山西长治 046012）

随车起重机（以下简称起重机）是重要的军民用产品，主要用于各种货物的吊装作业，本次研究对象为公司QH090型随车起重机，最大起重量为1300kg，最大幅度为6.2m。其臂架系统结构如图1所示。通过举升、动臂及伸缩油缸的运动，使起重机臂架达到规定幅度进行起重作业。其中，动臂油缸（以下简称油缸）系统一般分为2种机构形式，即3铰点机构和5铰点机构，本起重机油缸的设计方案为3铰点形式。本文通过对2种铰点机构的优化对比分析，详细比较2种机构的运动、力学性能，为起重机及其它类似产品的设计提供有效参考。

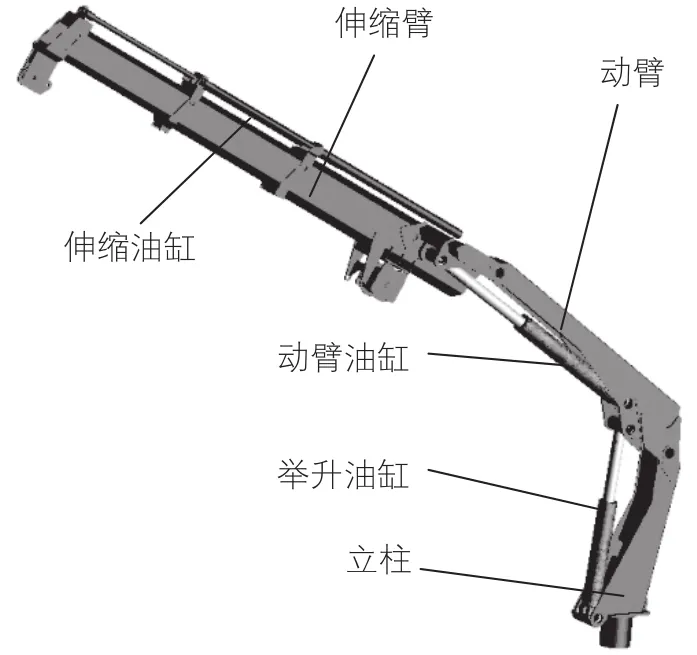
图1 QH090起重机臂架系统模型

1 油缸铰点机构受力模型

取动臂及伸缩臂为水平状态时为危险工况进行研究，设伸缩臂对动臂形成的弯矩为M，则3铰点形式下油缸处局部结构如图2所示。其中，O为伸缩臂与动臂连接点，A为油缸前铰点，B为油缸后铰点。

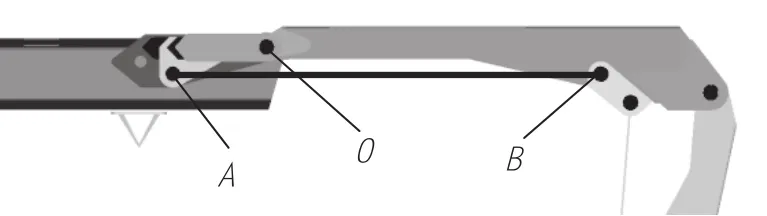
图2 3铰点形式油缸

此时油缸受力FAB为

将机构转化为5铰点机构，在此机构形式下，油缸处局部模型如图3所示。其中，O为伸缩臂与动臂连接点，CD为连杆1，DE为连杆2，D为油缸前铰点，F为油缸后铰点。此时油缸受力FDF为

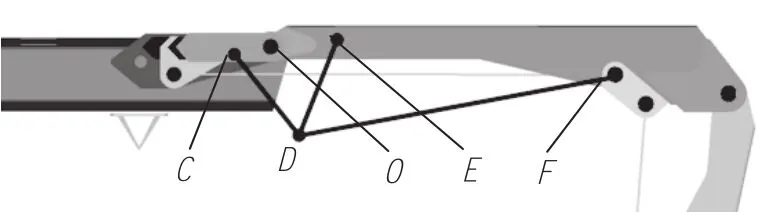
图3 5铰点形式油缸

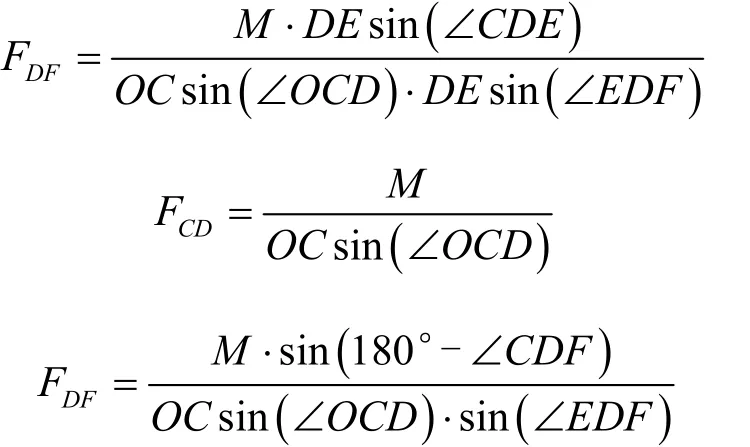
2 3铰点机构油缸受力优化

采用ADAMS2012中的优化模块，分别建立3铰点机构和5铰点机构的优化模型，对油缸受力进行优化。

2.1 设计变量

优化时取伸缩臂水平及折叠2种状态（即油缸分别为最长及最短）进行研究，伸缩臂转角为140°，设伸缩臂折叠时，图2中A点对应铰点为G，虚线为伸缩臂折叠状态，如图4所示。

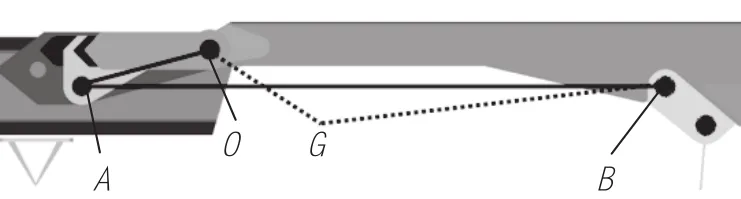
图4 3铰点机构优化模型

取伸缩臂转动点O为定点，A、B、G 3个点的横纵坐标为设计变量V1，即

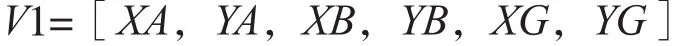
各设计变量的取值范围应以不发生结构干涉为前提，在此不再赘述。

2.2 约束条件

（1）应保证A、G相对于O点的距离相等，即

（2）为保证油缸安装，油缸最小长度去除油缸行程后，应大于某固定值，此处设定为290mm，即

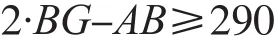
（3）应保证油缸由最短伸长至最大时，伸缩臂的转角为140°，即

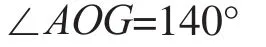
（4）为满足伸缩臂顺利展开条件，应保证

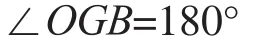
2.3 优化目标

优化目标为油缸受力最小，设优化目标为J1，则优化目标可定义为

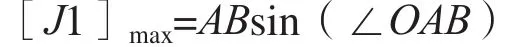
2.4 优化结果

设O点为坐标原点，则优化前后A、B点坐标如表1所示。

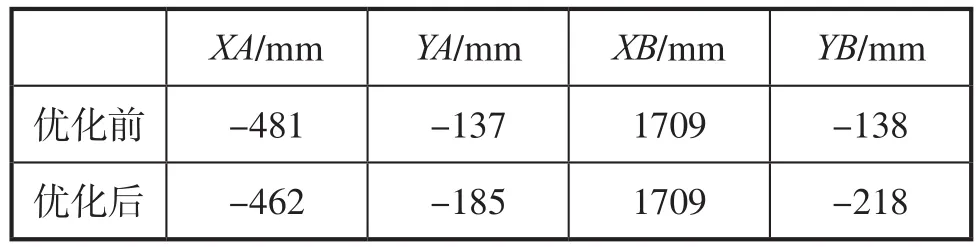
表1 3铰点机构优化数据

3 6铰点机构油缸受力优化

3.1 设计变量

同理，优化时取伸缩臂水平及折叠状态进行研究，设伸缩臂折叠时，图3中C点对应铰点为H，D点对应铰点为K，其中，虚线为伸缩臂折叠状态。

图5 5铰点机构优化模型

仍取伸缩臂转动点O为定点，C、D、E、F、H、K 6个点的横纵坐标为设计变量V 2，各设计变量的取值范围应以不发生结构干涉为前提，可得

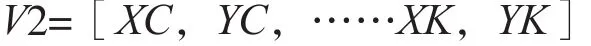
3.2 约束条件

（1）应保证C、H相对于O点的距离相等，D、K相对于E点距离相等，C、D距离与H、K距离相等，即

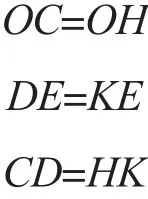
（2）油缸安装条件同上，如下式

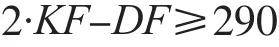
（3）伸缩臂转角同上，如下式

∠COH=140°

（D4F）为保证伸缩臂顺利展开，应满足

3.3 优化目标

优化目标为油缸受力最小，设优化目标为J2，则优化目标可定义为

3.4 优化结果

设O点为坐标原点，则优化后C、D、E、F点坐标如表2所示。

表2 5铰点机构优化数据

4 仿真分析

为验证优化前后及不同铰点机构的性能，采用ADAMS对起重机进行仿真分析，进而对比其各项性能参数。

4.1 仿真模型及参数设置

由于起重机起重工况较多，选取伸缩臂为水平工况重点研究，此时伸缩臂对动臂产生的弯矩M为最大值，为方便分析，计算时将伸缩臂固定为水平状态，弯矩M反向施加于动臂上，动臂与伸缩臂之间夹角由0°变化至65°，此范围可以覆盖起重机起重性能表内的所有工况。设吊装重量为P，载荷作用点距转动点O的水平距离为L1，伸缩臂自重为Q，质心距O点水平距离为L2，则M可写为

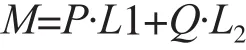
针对优化前的3铰点机构、优化后的3铰点机构和5铰点机构（分别记为算例1、算例2、算例3）进行对比分析，为方便计算，设M=5000t·mm，油缸匀速运动，速度为10mm/s，各算例中基本参数如表3所示。

在ADAMS中建立3个算例的仿真计算模型，各部件之间的运动副关系见表4及表5。

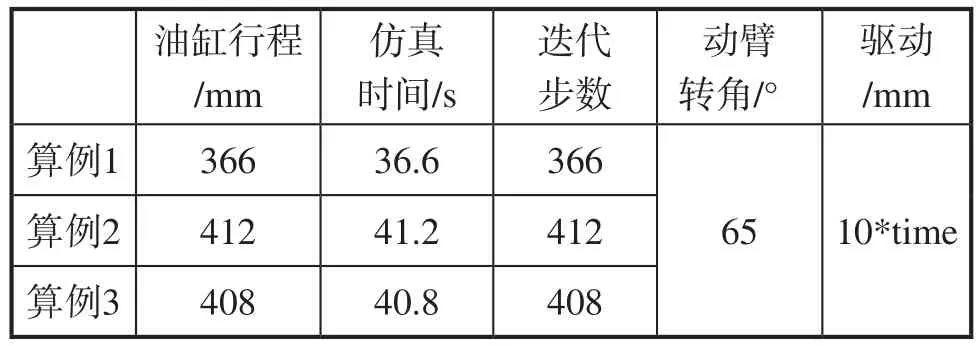
表3 各算例基本参数表

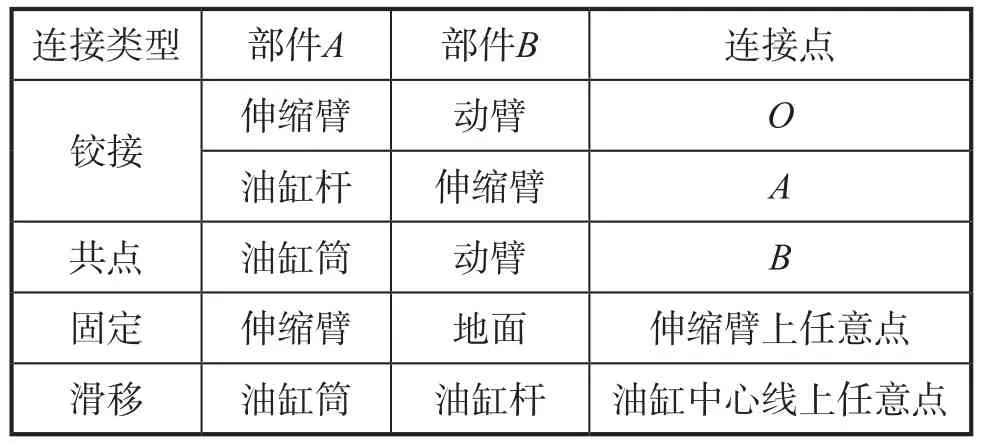
表4 算例1、算例2运动副情况

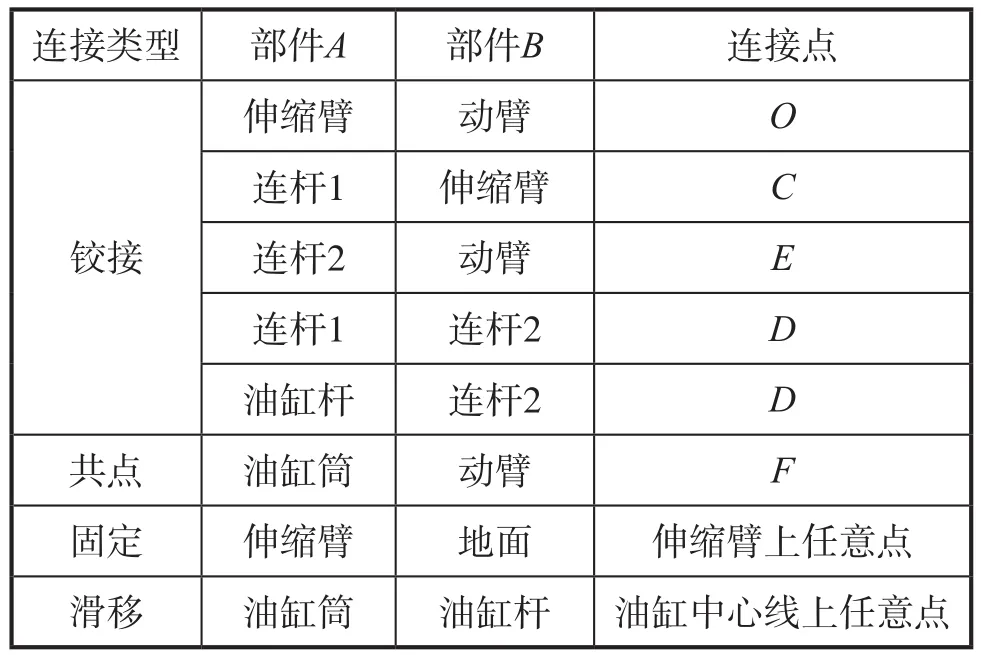
表5 算例3运动副情况

4.2 仿真结果分析

通过计算分析，得到3个算例中的油缸受力、动臂转角、角速度及角加速度等特性，见图6—图9所示。

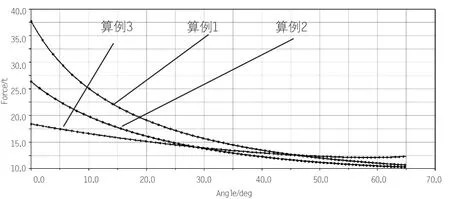
图6 各算例油缸力—动臂转角特性

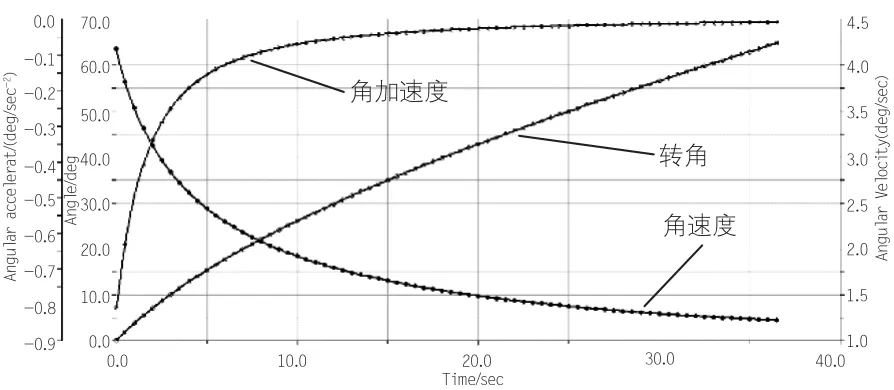
图7 算例1动臂转角、角速度、角加速度特性

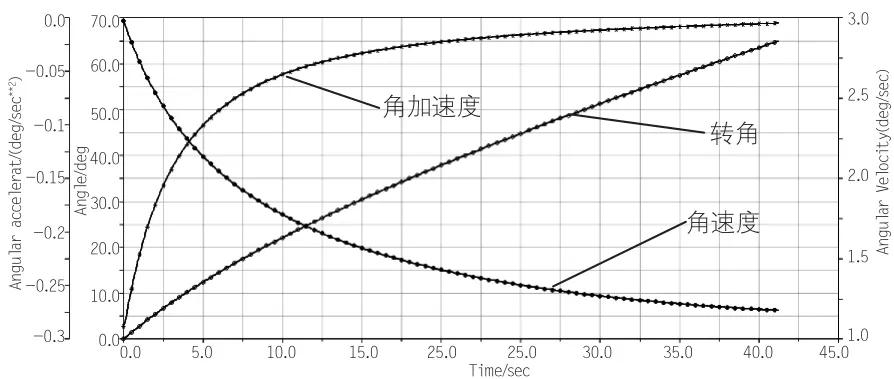
图8 算例2动臂转角、角速度、角加速度特性

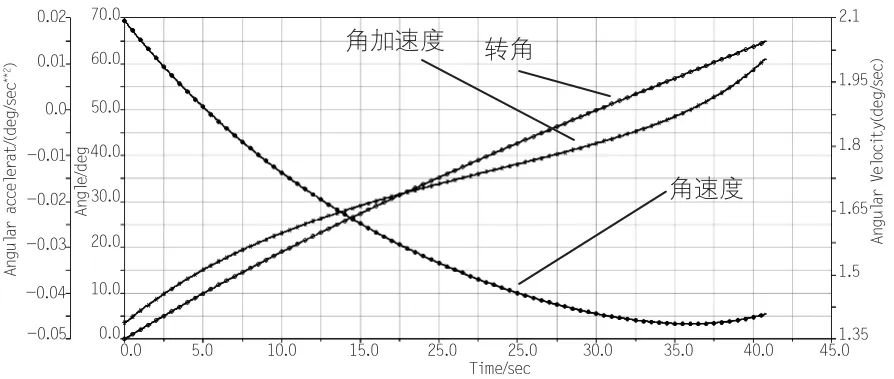
图9 算例3动臂转角、角速度、角加速度特性

（1）分析图6可知，3个算例中，油缸受力随着转角增大而降低。算例1油缸最大受力为37.7t，最小受力为10.6t；算例2油缸最大受力为26.4t，最小受力为10.3t；算例3油缸最大受力为18.4t，最小受力为12.1t。对比优化前后数据，经优化后的3铰点机构油缸最大受力降低率为30%，5铰点机构油缸最大受力降低率为50%。

（2）3个算例的油缸行程分别为366mm、412mm和408mm，在相同的油缸运动速度下，算例1臂架展开速度最快，算例3次之，算例2最慢。

（3）分析图7—图9可知，算例1动臂转角最大加速度为-0.81deg/s2；算例2转角最大加速度为-0.29deg/s2；算例3转角最大加速度为-0.046deg/s2，相比之下，经优化后的5铰点机构角加速度最小，臂架运动较平稳，结构冲击小。分析3个算例的动臂角速度，算例1最大角速度为4.17deg/s；算例2最大角速度为2.98deg/s；算例3最大角速度为2.1deg/s。可知经优化前，起重机臂展速度较快，易对周边人员造成危险，优化后的两种机构形式臂展速度均有明显降低。