基于测度的广义覆盖粗糙集模型*

夏秀云 田 浩 田时宇

（1.湖南信息学院公共课部 长沙 410005）（2.湖南信息学院电信学院 长沙 410005）

1 引言

粗糙集理论［1］是1982年波兰数学家Pawlak首次提出来的，它是集合理论的一种延伸。该理论是用来处理模糊以及不确定性的知识，已经广泛用于人工智能、模式识别、数据库的知识发现和专家系统等方面［2～4］。粗糙集模型由于是基于确定性知识库的，忽略了可利用信息的不确定性，有学者将概率测度引入粗糙集理论形成了概率粗糙集［5］，近年来其得到了广泛的应用和发展［6～7，9，11］。目前概率粗糙集模型的研究方向主要有两个方面，一方面是从关系方面进行拓展，将论域上的二元等价关系推广到相似关系、一般的二元关系和模糊关系等进行研究；另一方面是将概率测度推广到其他测度的粗糙集模型。例如，刘耀辉［8］于2010年提出了基于模糊测度和模糊积的粗糙集模型；覆盖［12～15］作为划分的一种推广，可以为粗糙集处理更复杂的数据形式提供方便。例如，孙秉珍［16］等学者通过设定参数α在置信区间，建立了变精度概率粗糙集模型；王美云［17］通过限定α，变两个参数为一个参数来研究基于覆盖的概率粗糙集模型；然后单雪红等［18］学者从另外的角度出发，借助偏序关系来研究覆盖粗糙集模型的特殊性质；接着，刘敏等［19］学者则从一个论域推广到两个论域上来研究覆盖变精度粗糙集模型；而薛占熬［20］等学者从覆盖的角度提出了基于Sugeno测度的粗糙集模型，又为粗糙集模型的推广研究指明了一个方向；刘财辉等［21］学者结合条件概率并利用元素的最小描述并集，研究了多粒度覆盖粗糙集模型。当然，关于覆盖粗糙集模型的进一步研究还有很多［22～29］，比如有借助邻域的［22］，有与直觉模糊集结合的［23］，有研究两个论域的［24］，有通过精度与程度或的［25］，有借助正负域讨论的［26］等。但对于基于模糊测度来研究广义的覆盖粗糙集模型还很少，故基于此，本文提出了基于测度的广义覆盖粗糙集模型。文中首先提出基于模糊测度的覆盖粗糙集的基本知识，然后构造了一种基于测度的变精度覆盖粗糙集模型以及证明其相关代数性质，紧接着讨论该模型的粗糙逼近问题，最后讨论了其近似精度和粗糙度，在一定程度上促进概率覆盖粗糙集模型应用范围，故本文的研究工作还是具有一定意义的。

2 预备知识

定义1［1，12］设U 为非空有限集合，称为论域。π是U的一个集类，如果π中的子集非空且∪π=U，则称π是U的一个覆盖，称有序对(U，π)为覆盖近似空间。

定义3［1］设U是有限非空的论域，称P∶2U→[0，1]为概率测度，如果

定义4［2］设非空有限论域U，论域U中的覆盖π，概率测度P建立在U的子集构成的σ代数上，md(x)为 x∈U 的最小描述，记ω=(U，π，P)为覆盖概率近似空间，限定 12＜α≤1，∀X⊆U，分别称

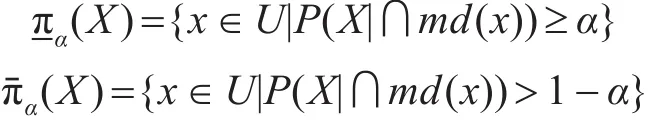
为X关于ω=(U，π，P)依参数α的上、下近似。

定义5［10］设 X是一非空集合，ψ是由 X的子集组成的非空类，Δ是定义在ψ上的非负实值集函数。称Δ满足（在ψ上）ν-r律当且仅当存在r∈（-supΔ-1，∞）∪{0}，使得下式成立。

其中，{Fm}是ψ中的集合构成的任意不交序列，且这些集合的并仍然在ψ中。

定义6［10］设h是 X上的子集组成的 ν代数。称Δ为h上的Sugeno模糊测度，当且仅当Δ满足ν-r律，且Δ（X)=1，简记为dr测度。

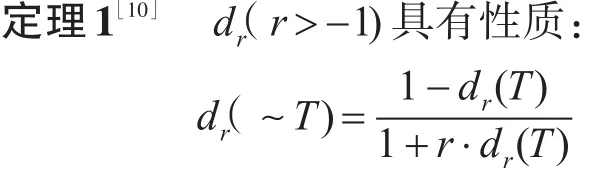
证明 参考文献［10］，略。

定义7［8，20］设U 是有限对象构成的论域，R是U上的等价关系，其构成的等价类为U/R={X1，X2，…，Xm}，仍记 x 所在等价类为 [x]R，令 dr为定义在U的子集类构成的ν代数上的Sugeno测度，三元组Tr=(U，π，dr)称为Sugeno近似空间，U中的每个子集称为概念，代表了一个随机事件。设0≤β＜α≤1，对 于 任意 X⊆U ，定 义 X 关 于Tr=(U，π，dr)依参数 γ，α，β 的Sugeno（I）型下近似 -dIα(X)和上近似 -dIβ(X)如下：

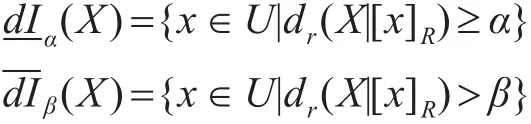
X 关于 Tr依参数 r，α，β 的Sugeno（I）型正域、负域和边界域分别为

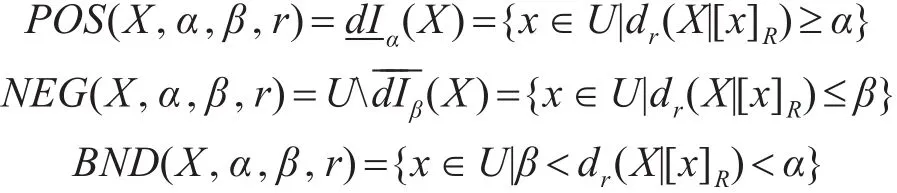
3 基于模糊测度广义覆盖粗糙集近似

定义8设U是有限对象构成的论域，π是U上的一个覆盖，令dr为定义在U的子集类构成的ν代数上的模糊测度，md(x)为x∈U的最小描述，三元组Tr=(U，π，dr)称为覆盖模糊近似空间，U中的每个子集称为概念，代表了一个随机事件。设＜α≤1，对于任意 X⊆U，定义 X关于模糊近似空间Tπr=(U，π，dr)依参-数r，α 的广义覆盖粗糙下近似 -dπα(X)和上近似 dπα(X)如下：

X关于Tπr依参数r，α的广义覆盖粗糙集正域、负域和边界域分别为

在以上的定义中，即U是非空论域，R是等价关系，则U的划分U∕R=｛［x］R|x∈R｝为U的一个覆盖，即∩md（x）=［x］R，对于任意X 包含于U：

定理2设模糊近似空间T=(U，π，d)，＜πrrα≤1，则 X关于Tπr依参数α的下近似和上近似满足以下性质：

证明 由定理2 6），易证，略。

推论2设T=(U，π，d)，∀X，Y⊆U，＜α≤1，πrr则X关于模糊近似空间Tπr依参数α的正域、负域和边界域满足下列性质：

注 当 X=U，由定理1和推论2可知，POSπ(X，α，r)=U， NEGπ(X，α，r)=∅ 和BNDπ(X，α，r)=∅ ；当 X=∅， POSπ(X，α，r)=∅，NEGπ(X，α，r)=U ；BNDπ(X，α，r)=∅ 。故对于Tπr=(U，π，dr)，其对应的正域 POSπ(X，α，r)、对应得 负 域 NEGπ(X，α，r) 以 及 对 应 的 边 界 域BNDπ(X，α，r)构成U 上的划分。

4 广义覆盖粗糙集上下近似的粗糙逼近

5 广义覆盖粗糙集的近似精度和粗糙度

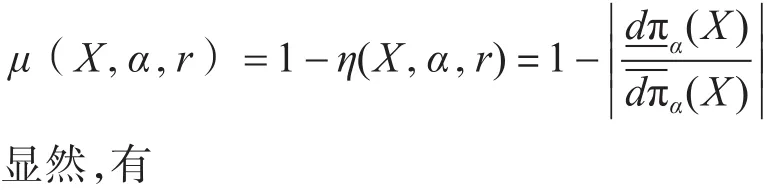
0≤η（X，α，r）≤1，0≤μ（X，α，r）≤1

若X是依参数r，α是可定义的，当且仅当粗糙度 μ（X，α，r）=0，近似精度 η（X，α，r）=1。

设 Tπr=(U，π，dr)为覆盖模糊近似空间，对∀X⊆U，0.5＜α，α1，α2≤1，有

由上面的性质可知，广义覆盖粗糙集的近似精度关于参数α是单调减少的，其粗糙度关于参数α是单调减少的。

定理6 设Tπr=(U，π，dr)为覆盖模糊近似空间，{αn}∞n=1是一个数列，且 αn∈(0.5，1]。对于任意X⊆U。

1）若{αn}∞n=1单调增加，则

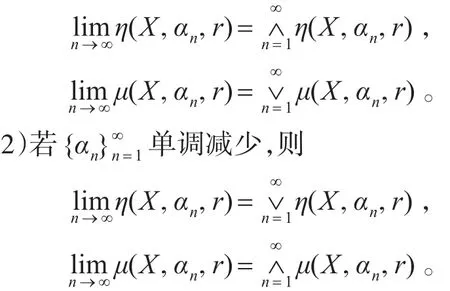
由 η(X，αn，r)和 μ(X，αn，r)的关系可得

同理可证结论2）。

推论3 设Tπr=(U，π，dr)为覆盖模糊近似空间。{αn}∞n=1是一个数列，且αn∈(0.5，1] 。 对 于 任 意 X⊆U ，令βn=1-αn∈[0，0.5)。

1）若{αn}∞n=1单调增加，则

6 结语

对论域进行分类时，一般得到的论域是一个覆盖，本文在结合目前已有覆盖粗糙集、变精度粗糙集、概率粗糙集和Sugeno测度粗糙集模型研究的基础上，提出了基于模糊测度的广义覆盖粗糙集模型，讨论了其性质和定理，从而能够充分利用模糊近似空间中尽可能多的有用信息，比较客观、准确地反映了被认识对象的本质属性以及数据之间的相关性，进而使近似决策的精确性更高。