基于改进遗传算法的PID参数整定研究*
2019-01-02王文庆
王文庆 杨 楠
(西安邮电大学自动化院 西安 710121)
1 引言
遗传算法(GA)[1]是一种基于生物进化模拟的启发式智能优化算法,主要由Holland教授从20世70年代逐渐发展起来,其基本策略为将生物的种群代表一组实际问题的解,然后对此种群进行选择、交叉、变异等操作获得新生种群,逐渐接近最优解[2]。
自从PID控制器生产以来,就成为自动化生产过程中使用频率最高、使用范围最广的控制器[3]。在控制领域之中,尽管各类型新型控制器层出不穷,但PID控制器依旧因为自身结构原理简单、适用性强、鲁棒性强等突出的优点[4],处于主导地位。由于PID控制器的比例参数、微分参数、积分参数可以直接影响控制器控制效果的优劣[5],所以参数整定即为PID控制器设计的核心问题[6]。
将传统PID与智能控制算法相结合,从而可以产生许多的改进型PID控制器[7]遗传算法作为一种新型的智能控制算法[8],其本质上是一种较为高效、并行、全局搜索的方法[9],但是由于标准遗传算法中遗传算子的静态特征不能满足种群的动态进化要求;交叉概率和变异概率的固定造成搜索过程较为迟缓和难以产生新个体[10],从而使得算法产生趋于局部最优和收敛精度不高等问题[11]。本次研究使用改进的遗传算法在Matlab中进行PID参数整定,并选用典型受控对象,进行仿真,进一步验证。
2 遗传算法的基本概念和应用步骤
2.1 遗传算法的基本概念
编码:通过某种编码方式将染色体抽象为跟编码方式对应的特定符号,并且为按照一定顺序排成的串。
适应度:对染色体进行编码后,每个个体对应一个具体问题的解,每个解对应一个函数值。函数值为适应度,函数为适应度函数。适应度值大小是遗传算法对于一个个体好坏程度的唯一评价标准。
复制:从父代中选择适应度值高的字符串从而生成新一代的过程。适应度值越高的字符串越可能获得生成新一代的可能[12]。
交叉:模拟生物进化中的繁殖过程,两个染色体之间通过交叉而重组形成新染色体,从而产生新的优秀品种。
变异:模拟生物进化[13]过程中的基因突变方法,以很小的概率随机地改变染色体字符串某一位的值。
2.2 遗传算法的应用步骤
1)确定可以表示可行解的染色体编码方法,从而产生初始种群。
2)确定个体适应度函数,计算个体适应度值,适应度值高的个体被选择的概率高。
3)设计选择算子,交叉算子,遗传算子从而进行遗传操作。
4)设计终止条件,如果满足终止条件,则进入第5)步,否则重新计算其适应度。
5)输出种群中适应度最高的值作为最优解。基本遗传算法的5个运行参数[14]:
M:种群的大小,即群体所包含个体的数量,一般可以取20到100;
G:代沟,即两代之间不相同的染色体数目,无重叠G=1,有重叠0<G<1;
Max Gen:终止进化代数,一般可以取100到1000;
Pc:交叉概率,一般可以取0.4到0.9;Pm:变异概率,一般可以取0.0001到0.1。
3 改进的遗传算法
3.1 编码及初始种群的产生
基本遗传算法采用的是二进制编码,所以其编码解码操作简单便捷,且选择、交叉、变异等遗传操作易于实现。然而,面对一些精度要求很高的、多目标的连续函数优化时,二进制编码有其局限性。例如,从某字符串表示的解到一个临近的解的转变,需要多次改变多个位的字符即海明悬崖;越高的精度,需要越长的字符串,增加了遗传算法计算的复杂性。为了改进这些问题,本文采用浮点数编码进行编码,浮点数编码是指个体的每个基因值用某一范围内的一个浮点数来表示,个体的编码长度等于决策变量的个数。本系统中有三个待优化参数Kp,Ki,Kd,可将三个参数组合成一个三维向量,作为遗传算法中每个独立的个体,其中0≤Kp≤20,0≤Ki≤1,0≤Kd≤1。定义染色体编码如下:

其中 Kp,Ki,Kd分别表示 PID 控制器的比例参数,积分参数,微分参数;G表示个体。
3.2 计算适应度
适应度函数是用来区分种群中个体好坏的唯一标准。遗传算法在进化搜索中,以适应度函数作为唯一依据,利用种群中每个个体的适应度值来进行搜索。作为参数选择的最小目标函数选用误差绝对值时间积分性能,加入输入的平方项[15]从而防止控制能量过大。可令目标函数为如下的形式:

其中e(t)为系统误差,u(t)为控制器的输出,w1,w2,w3,为权值,tu为调节时间。
由于遗传算法需要的是适应度函数,所以需要将目标函数改为适应度函数,它的数值是大于等于0的,并且其值越大越容易被认可。对于不同的问题,适应度函数定义的方式也不同,本次研究采用适应度函数为

3.3 选择
此次研究采用均匀排序的方法,对群体中的所有个体计算其适应度,根据每个个体的适应度值占总体适应度的比例将这个概率作为适应度概率。概率如下所示:

其中Fcx为某代第x个个体的适应度值,F∑为某代所有个体的适应度之和。
此方法可有效避免适应度值高的个体被淘汰,以及随机排序中个体选择概率相同的情况。
3.4 交叉
对于那些被选择的个体,以某种交叉方式交换两个字符串相对应的基因,从而产生两个新的个体,新的个体组合其父代的特点,采用算数交叉的方法,交叉后相邻的第i个个体和第i+1个个体如下:

其中Pc1=0.9,Pc2=0.6。
3.5 变异
在群体中随机选择一个进行过交叉的个体,以一定的概率随机改变被选择个体字符串中某字符的值,变异概率如下:

其中,为每代平均适应度,为群体中最大适应度,为要变异个体的适应度值,为交叉的两个个体中较大的适应度值;β∈[0 1]为一个随机数;kpmax和kpmin分别为基因kp的上限和下限;kimax和kimin分别为基因ki的上限和下限;kdmin和kdmin分别为基因kd的上限和下限。
4 PID控制器
4.1 典型的PID控制器
PID控制是一种线性控制方法,对偏差信号进行比例、积分、微分运算,将三种运算的结果相加,就得到PID控制器的输出【10】。其原理框图如下:

图1 PID控制原理框图

也可将其改写为传递函数形式:

其中:r(t)为输入,e(t)为设定输入与实际输出的差,u(t)为控制器输出,y(t)为系统输出,kp为比例参数,Ti积分时间常数,Td为微分时间常数,积分参数 ki=kp/Ti,微分参数为 kd=kp*Td,kp、ki、kd即为本文中的寻优参数。
4.2 基于改进遗传算法的PID控制器设计
改进的遗传算法模块和典型PID控制器构成了改进遗传算法的PID控制器。PID控制器对控制对象进行闭环循环控制,改进的遗传算法模块依据系统的运行参数,不断进行计算以此优化三个参数的数值,直到计算出最优参数。改进的遗传算法模块将 PID 控制器的 Kp,Ki,Kd,三个参数组合在一起作为改进遗传算法的每个独立个体。根据遗改进的传算法流程进行编码,对种群进行选择、交叉、变异操作,当种群不断迭代繁殖,直到找到全局最优解。
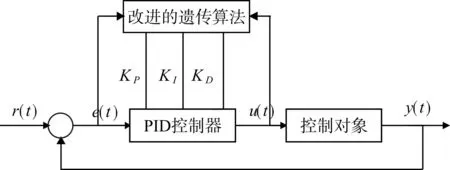
图2 改进的遗传算法PID控制器设计图
5 仿真实验结果
基本遗传算法PID参数整定仿真结果如下图3、图 4 所 示 ,其 中 Kp=18.7069,Ki=0.2463,Kd=0.6443。

图3 基本遗传算法PID阶跃响应图
改进的遗传算法PID参数整定仿真结果如图5和 图 6所 示 ,其 中 Kp=18.4772,Ki=0.2348,Kd=0.0229。

图4 基本遗传算法目标函数值优化曲线
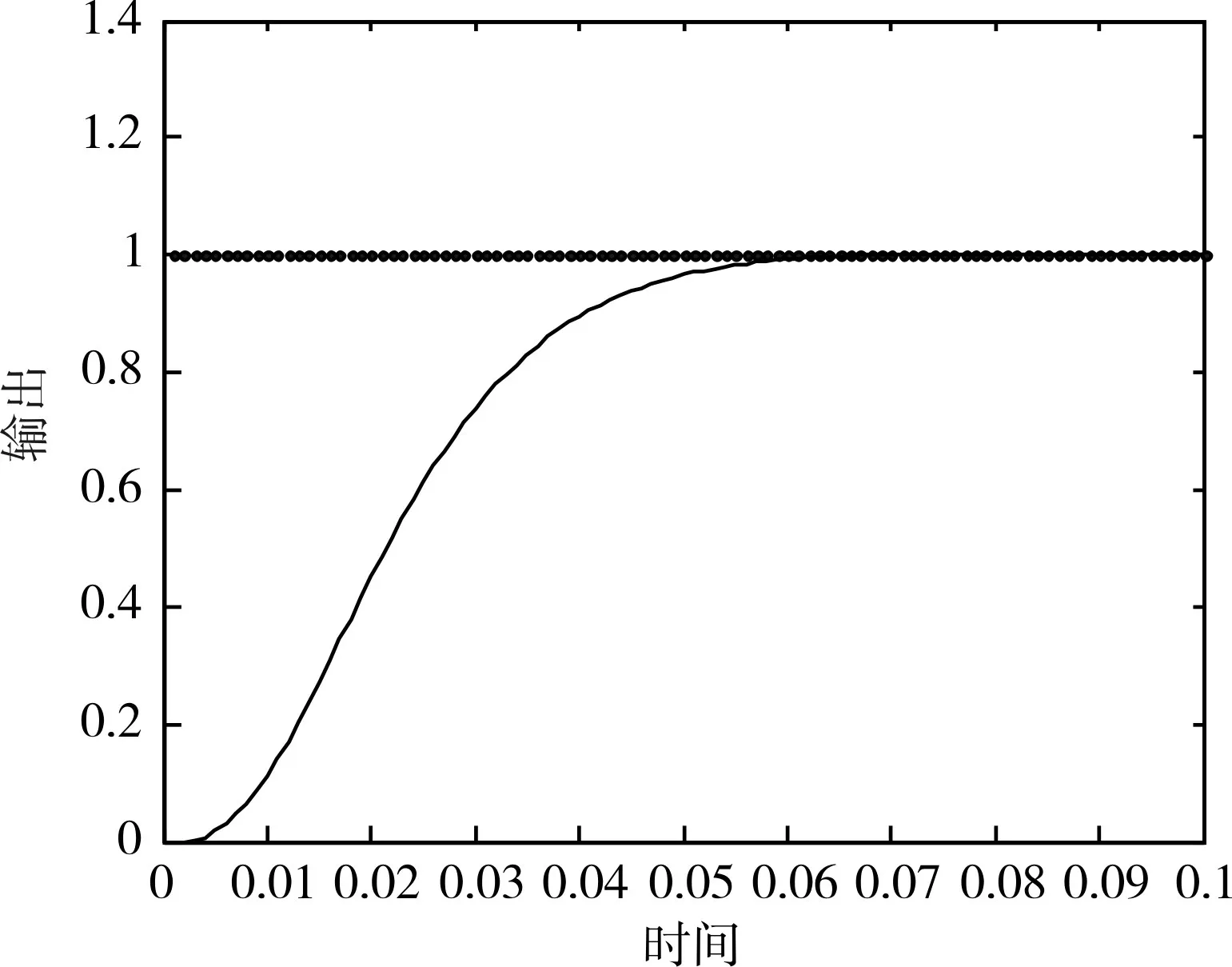
图5 改进遗传算法PID阶跃响应图

图6 改进遗传算法目标函数值优化曲线
根据以上仿真结果可知,本文中改进遗传算法一定程度上加快了整定速度,提高算法收敛精度,保证了优化效果,具有一定可行性。
6 结语
PID参数的设定是PID控制器设计的核心环节,本文在基本遗传算法基础上进行改进,并以改进的遗传算法与PID参数定相结合,在Matlab上进行仿真,实验结果可以表明:改进的遗传算法PID控制器要与基本遗传算法PID控制器相比较,有更快的整定速度,更精确的收敛精度,更良好的控制优化效果。
