一种改进的离散粒子群算法用于分布式电源容量优化*
2019-01-02钟腾飞
陈 岭 杨 静 钟腾飞 王 超
(1.中国人民解放军陆军勤务学院 重庆 401331)(2.中国人民解放军62160部队 华阴 714200)
1 引言
随着能源危机的日益临近和对微电网研究的深入,加之分布式电源具有发电方式灵活、安装位置分散、投资小、节能环保、靠近用户等特点,分布式发电有助于提高局部供电可靠性,在提高一次能源利用率的同时减少各种污染物的排放,还能够减少输电线路损耗。而在分布式电源优化配置中,合理的电源选型和定容是一个重要和复杂的问题,既要考虑其运行的系统性与可靠性,又要考虑系统的经济性[1]。
2 双子群离散粒子群优化算法
双子群离散粒子群优化算法(Double Sub-swarms Particle Swarm Optimization,DSPSO)主要特点是在James Kennedy等提出的二进制离散粒子群优化算法(BPSO)[2]的基础上,将其由原来单一子群搜索改进为由分别处于开发和探测状态的两个子群同时进行搜索,二者共同协作以提高算法求解精度并降低了陷入局部最优的危险。
二进制离散粒子群算法中,二进制粒子的位置变量被定义在离散的二进制空间中,通过速度来确定位置变量的每一位取值是0或1,位置与速度的关系可以描述如下:
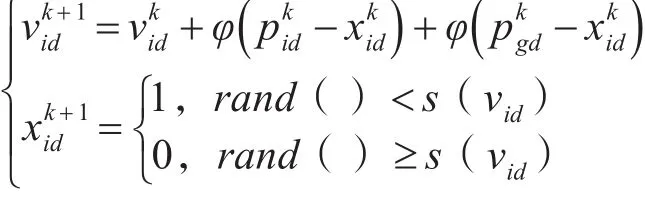
式中,rand()表示分布在[0,1]之间的随机数。函数、代表由速度vid决定的一个范围在[0,1]之间的概率函数,s越接近1,xid就越有可能取1,否则xid就越有可能被选择为0。文献[2]中将一种模糊函数Sigmoid作为概率函数,函数表示如下:

2.1 算法定义
为使二进制离散粒子群算法保持较快的收敛性的同时能够逃脱陷入局部最优的危险,这里定义开发状态和探测状态两种不同的粒子运动状态,并以此定义将原粒子群划分为开发子群和探测子群两个子群。其中,开发子群的粒子用以提高原粒子群粒子的局部寻优能力,而探测子群的粒子则以提高原粒子群粒子的全局寻优能力即避免陷入局部最优为目的。特定条件下,两个不同的子群间粒子能够相互“跳跃”。本文中这一改进的二进制离散粒子群算法即为“双子群离散(二进制)粒子群算法”,以下简称DSPSO。
为保证算法收敛速度,开发子群中粒子以“爬山法”思想更新其位置,即开发子群内粒子只能移动到比其原来具有更优秀适应度值的位置。处于探测状态的粒子则在经过一定迭代代数后,其位置信息将按位以“伪变异”概率变为子群中当前适应度值最优粒子的相应位置变量信息,此目的为保持探测子群的群体多样性,同时也为避免搜索陷入局部最优的危险。
2.2 算法模型
开发子群中粒子对当前全局最优位置附近进行进一步的考察探索,而探测子群可对未开发领域进行开发探索,两个子群在动态过程中通过相互间粒子跃迁和各自特有更新策略进行不断更新进而搜索到最终全局最优适应度值。算法具体实现步骤及相关公式如下:
1)初始化两个子群的规模、粒子位置、速度及其他相关参数变量。
2)若粒子运动状态满足由探测状态向开发状态转变的任一条件,则探测子群中粒子以概率ϕ向开发子群“跳跃”。
条件1:开发子群粒子数量N1不超过设定的最小值min N1;
条件2:探测或开发子群中任意粒子搜索到了新的全局最优值gbest,且gbest为“优秀极值”;满足以下公式的gbest称为优秀极值:

式中,k为全局最优值的序号,k起始值为1,全局最优值gbest更新时k=k+1。
3)若粒子运动状态满足由开发状态向探测状态转变的任一条件,则开发子群中粒子以概率ϕ向探测子群“跳跃”,并重新初始化探测子群中新进粒子的位置信息。
条件1:探测子群粒子数量N2不超过设定的最小值min N2;
条件2:种群中持续fspNum次迭代内没有新的“优秀极值”出现;其中fspNum为“优秀极值”出现的最大迭代间隔。
探测子群中新进粒子的位置重新初始化公式如下:

式中,rand()为即时赋予粒子的分布在[0,1]的随机数;xd,max与 xd,min为第d维搜索区域的最大值和最小值;函数U( )xd,min,xd,max代 表 分 布 在[xd,min,xd,max]之间的随机数。
4)若迭代代数达到探测子群粒子伪变异迭代间隔fmNum的整数倍,则探测子群中粒子执行伪变异操作。探测子群粒子伪变异公式如下:

式中,xi,d表示第i个粒子位置变量中的第d位;cm为伪变异率;rand()为即时赋予该位的[0,1]的随机数。
5)更新所有粒子的速度与位置信息。探测子群中粒子速度和位置更新公式如下:

7)重新评价开发子群中粒子的适应度值,并更新开发子群最优值和全局最优值信息。
8)重新评价探测子群中粒子的适应度值,并更新个体历史最优值和全局最优值信息。
9)若算法满足结束条件,则输出全局最优值gbest和对应的位置信息,否则进入步骤2进行下一次迭代。
3 微电网电源模型
假设微电网中电源和储能装置均以先进的电力电子装置为接口来接入微电网,并可以及时跟踪负荷、风能和太阳能出力等的变化,达到“即插即用”条件,能在并网与孤岛运行模式间平滑切换[3~4]。
3.1 风机模型
受风速随机性的影响,风力发电机出力也呈现随机性特点。采用分段函数近似表示如下:

式中,PW()v为风力发电机在风速为v时的输出功率;vci为切入风速,vco为切出风速,vr为风力发电机的额定风速;Pwtn为风力发电机的额定输出功率。一般地,当风速介于vci和vr之间时,风力机的输出功率可近似表示为与额定输出功率呈线性关系的函数。
3.2 光伏阵列模型
光伏发电与光照强度有关,也具有不确定性。光伏电池发电功率与环境温度、光照强度有关,其输出功率PV的计算公式为
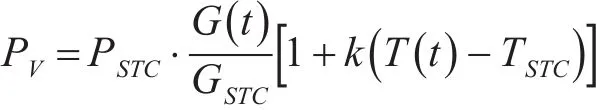
式中,PSTC、GSTC和TSTC分别为标准测试环境(1kW∕㎡、25℃)下的光照强度、最大输出功率和电池温度;k为温度系数;T(t)为t时刻的电池实际温度,其值可由该时刻的环境温度Ta(t)和辐照度G(t)表示:
刘晓璐等研究了近红外光谱无损快速检测蓝莓花色苷含量的技术,结果表明,在波长400-2500nm光谱范围内,应用偏最小二乘法建立蓝莓花色苷含量的定标数学模型,相关系数为0.7503,校正标准误差4.688mg/100g。说明近红反射技术可用于无损快速检测蓝莓中花色苷含量[33]。
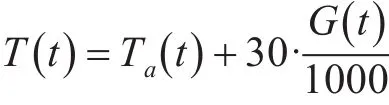
3.3 柴油发电机模型
柴油发电机发电一般是可控的,输出功率根据实际情况需要可在额定功率Pn-DG限额内变化。柴油发电机的燃料消耗与输出功率Pa-DG及额定功率间的关系为

式中,fuel为燃料消耗量(L∕h),αDG与 βDG为柴油发电机燃料消耗曲线系数;Pn-DG为柴油电机的额定功率(kW),Pa-DG为柴油发电机的实际输出功率(kW)。 本 文 取 αDG=0.081451L∕kWh,βDG=0.2461L∕kWh。
3.4 蓄电池模型
储能装置有多种类型,主要包括:蓄电池、飞轮和超级电容器等。其中蓄电池储能是目前应用最普遍、技术最成熟的储能装置。本文采用铅酸蓄电池(Lead-acid Battery,Pb)作为微电网电源规划的储能方式。其实际可用容量Ebat(t)与电池温度的函数关系可表示为[5]

式中:Tbat()t为工作点蓄电池温度,此时可近似为环境温度Ta(t);ESTC为标准条件下蓄电池的额定容量,由生产厂家提供;TbatSTC为25℃,δB为容量温度系数。
蓄电池在运行过程中满足满足公式:
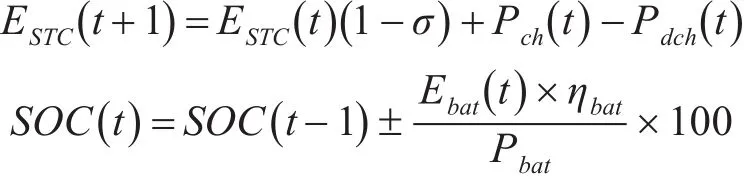
式中:σ为每小时蓄电池的自放电率;Pch(t)为充电功率;Pdch(t)为放电效率;SOC为电池充放电状态(State of Charge)是防止蓄电池过度充电或过度放电的一个重要变量。
4 微电网DG容量优化配置模型
为实现经济性与可靠性的协同优化,本文用停电损失函数[6]将多目标优化转化为单目标优化来进行。
4.1 目标函数
本文所建立的复合微电网电源优化模型主要包含风力发电机、光伏阵列、柴油发电机和变压器等,以及相关配套设备。模型将设备购置费、运行与维护费、燃料费以及从主网购电费和政府对新能源的电价补贴等五部分计入目标函数,以实现在满足使用可靠性的前提条件下达到系统等年值投资最少和初始投资收回年限最短的综合优化配置目标。
1)负荷年停电量期望
用户系统内部j类负荷同时由市政电网和微网并联供电,其中第j类负荷年停电量期望值EENS,j用下式表示:

式中,Ea,j0为原来单独由市政电网系统供电时第j类负荷年所需供电量(kWh);Lj0,h为第j类负荷在h时段所需功率大小(kW);αg,j指仅由市政电网独立向第j类负荷供电时该类负荷的缺电率;αMG,j指仅由微网独立向第j类负荷供电时该类负荷的缺电率。负荷缺电率(LPSP)是供电可靠性指标中的一种,定义为系统不能满足的负荷需求除以评估期内总的负荷需求[7],论文中评估期取1年。
2)系统等年值投资费用
本论文中并网型微网系统等年值投资费用公式为

式中,Cte为年总购电费用(Total Electricity Charge,Cte),CDER为分布式电源总费用等年值(CDER=CIGA+COMG+CFE,其中CIGA代表分布式电源初始投资等年值费用、COMG代表分布式电源年运行维护费用、CFE代表分布式电源年发电消耗燃料费用),G为政府在分布式电源建设并投入使用后以电价形式的长期补贴。
3)可靠性转化为经济性的总目标函数
以停电损失函数法将系统年停电损失费用CO与系统等年值投资费用结合,得到论文所用的总体优化目标函数min Cost,具体公式如下:

式中,CO为系统年停电损失;j=1,2,3分别代表重要纯电负荷(Eop)、一般纯电负荷(Eot)、冷负荷(CO)三类负荷;RIEA,j为第j类负荷单位电量损失费用,也称停电损失评价率IEAR,单位为元∕kWh,EENS,j为j类负荷年停电量期望值(Expected Energy Not Supplied,EENS),单位为 kWh∕年。
4)投资回收年限
假设工程使用周期为20年,以每年节约购电费用和对应的政府补贴两项费用之和来实现回收初始投资及后期投资。投资回收年限Y以在15年之内,年限越短越好。其中,投资回收年限是反映项目财务投资回收能力的重要指标,计算公式如下[8~9]:

式中:P0为初始投资,Rt为每年的净收益,Rt为投资回收年限。
4.2 约束条件
微网系统运行中需满足如下约束条件:
1)电源出力约束
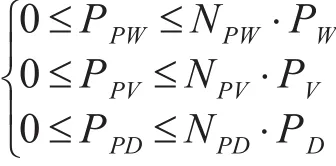
式中,PW为单台风机的额定功率,PV为单台光伏组件的额定功率,PD为单台柴油发电机的额定功率。
2)蓄电池充放电约束[10]
任意时刻蓄电池的电量不能超过其所能储存能量的上下限。

式中,SOC(t +1)为t+1时刻电池储存的电量,Pbat(t)为某时刻蓄电池充放电功率(充电为正,放电为负)。
3)供电可靠性约束

式中,fLPSP为年缺电率,fmax为系统允许的最大年缺电率。
4)功率约束[11]

其中,PL(t)为负荷功率,Pg(t)为联络线功率(向配电网输送功率为正)。
5)分布式电源接入约束
本文按照《分布式电源接入电网技术规定》和《配电网技术导则》中的相关要求,或将其转换为配电网对微电网接入的要求。
(1)分布式电源总容量原则上不宜超过上一级变压器供电区域内最大负荷的25%[12];
(2)8kW及以下可接入220V电压等级;8kW~400k W可接入 380V 电压等级[13];
(3)分布式电源并网点的短路电流与分布式电源额定电流之比不宜低于10[12];
对于以分布式电源方式接入,PCC处的最大功率波动一般小于等于其额定容量,若采用微电网接入方式,PCC处短路电流不低于联络线最大电流的10倍,可近似认为:与微网联络线功率等效的分布式电源额定容量须小于PCC短路容量的10%,即|Pg(t)|≤10%×SSC,其中SSC为PCC短路容量。
5 算例分析
5.1 算例描述
根据以上所建立模型,选取青海省西宁市某县医院(东经101°16′,北纬36°40′)作为研究对象。根据该县医院2015年全年的电力负荷,结合该县城当年全年的风力、光照、温度等气象条件,应用DSPSO算法对其进行计算,以验证论文所提算法和模型的有效性。据统计,该医院负荷平均耗能892.82kWh∕d、平 均 功 率 37.2kW、峰 值 功 率70.05kW,负荷曲线如图1所示。该医院所接入台区变压器容量为2000kVA。参考该县气象局所提供的气象数据,借助于HOMER软件,根据风速的威布尔分布统计特性,将月平均风速处理拟合得到全年每小时的风速数据,数据曲线如图2所示,全年光照强度数据曲线如图3所示。

图1 系统全年负荷数据曲线
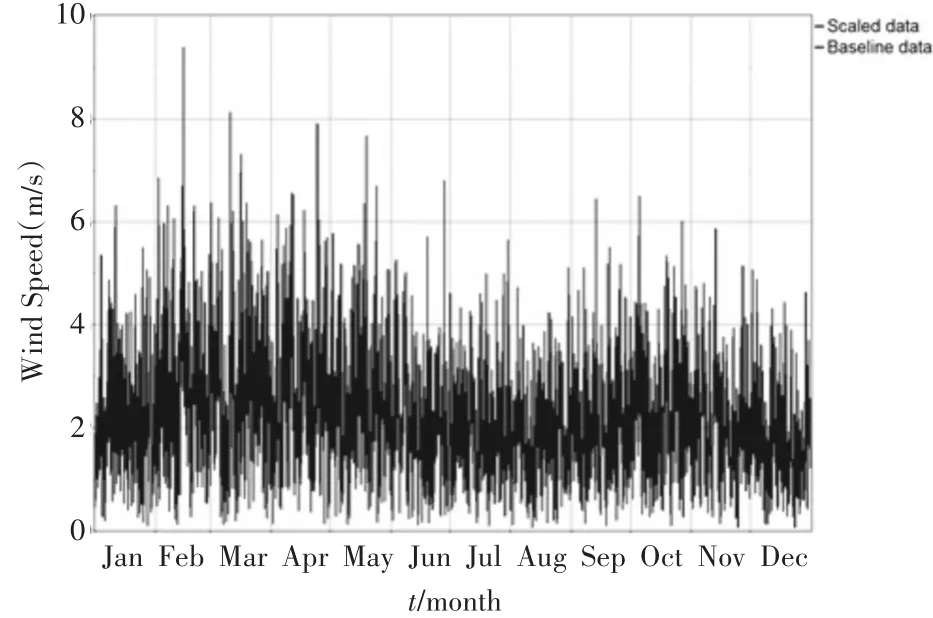
图2 微网所在地全年风速曲线

图3 微网所在地全年光照强度曲线
5.2 计算结果
假定工程寿命周期为20年,论文进行的仿真运行时间定为1年,运行步长为1h,用matlab2016a进行编程和仿真,结合微网所在地2015年的气象数据,利用第4章中DSPSO算法对第3章所建立的模型进行优化计算,算法中所用到的参数见表1,相关分布式电源经济参数(数据部分选自[5,14~15])见表2。整个微电网系统主要考虑满足医院自身负荷用电需求,以并网微电网分布式电源自发自用形式进行DG配置。通过计算,求解得到对该医院建设并网型微电网系统的等年值投资成本。

表1 算法参数设置

表2 分布式电源经济参数
通过计算求出分布式电源及相关设备配置容量和等年值投资与投资回收年限,如表3。
5.3 结果分析
风电、光伏发电受自然因素影响较大,柴油发电机主要在市政电网和可再生能源发电不能满足不能满足重要负荷供电或紧急情况下启用。结合各DG的约束条件和功率上限以及不同等级负荷的大小,根据气象条件得出该配置方案。离散型算法的结果更方便DG容量配置,便于整数规划问题的求解。

表3 计算结果
6 结语
本文提出了采用双子群离散离子群算法对微网中分布式电源优化配置问题的求解方法,建立了计及购电成本、设备投资成本、运行维护成本和政府补贴等的微网DG优化配置模型,综合考虑了风光等自然资源随机性和波动性特征,以及蓄电池的充放电特性对并网并网微网中DG配置的影响。并结合具体算例中供电可靠性要求和备选电源种类,得到相应的微网DG配备容量的最优配置方案。本文设计的并网型微电网系统模型,较好地补充了以往多从投资商或独立用户角度考虑,以发售电盈利为目的的微网建设模型,为建立更加多元的微网模型系统提供了有益思路。
