多反馈混合模式振荡介质中超结构行波的模拟与分析

唐晓栋

(徐州医科大学化学教研室，江苏徐州 221000)

斑图是自然界普遍存在的一种时空现象，是在空间或时间上具有一定规律的非均匀结构［1－2］，大到银河系，小到细胞内的钙离子波［3］，无论是植物的叶序排布还是动物表皮的斑纹，甚至在星球表面的地纹排布都是各种斑图结构。而在化学反应系统内的斑图可分为两类［4］:一类是热力学平衡条件下的斑图，如化学物的晶体结构等;第二类则是在远离热力学平衡态的情况下形成的耗散结构斑图，其中最典型的就是在化学反应－扩散系统中的化学波。近期研究表明［5－6］，在具有复杂化学振荡模式的体系中，通过扩散系数的改变，会浮现出具有丰富模式变化的化学波现象。本文选用一个经典三变量模型，采用一维斑图模拟的形式，得到了具有稳定传播的一维行波，并发现在混合模式区域会出现具有超结构现象的复杂时空斑图。

1 研究模型介绍

本文所采用的数值模拟方程是Hasting－Powell反应扩散模型［6－7］(以下简称 HP 模型):

其中，u，v和w分别为系统内的三个组分变量，而a1、b2、a2、b2、d1和 d2则是模型的六个动力学参数，Du、Dv和 Dw分别表示系统的三个变量的扩散系数。本文中参数的取值范围见表1。该模型可以用于模拟具有多个反应物的连续反应，其中u可视为反应底物，而v和w则分别对应着反应的一级产物和二级产物。

表1 HP反应－扩散模型的参数取值范围

2 模型均相动力学分析

通过针对该模型进均相动力学分析，我们发现HP模型可以表现出多种复杂模式的动力学行为，如简单振荡、倍周期振荡、混合模式振荡和混沌现象。图1给出了在a2－b2参数区间内计算得到的Lyapounov指数相图，为了便于辨别和分析，图中选取了两种不同颜色标尺来分别表征Lyapounov指数大于零(暖色)和小于零(灰度)的区域。图中Lyapounov指数等于零或接近于零的点，即HP模型的分岔点，可以在参数空间内构成分岔曲线，每当系统的动力学参数的变化跨越分岔曲线就表示系统的动力学模式发生了改变。根据分岔形式的不同，HP模型中的分岔曲线可以分为两种:

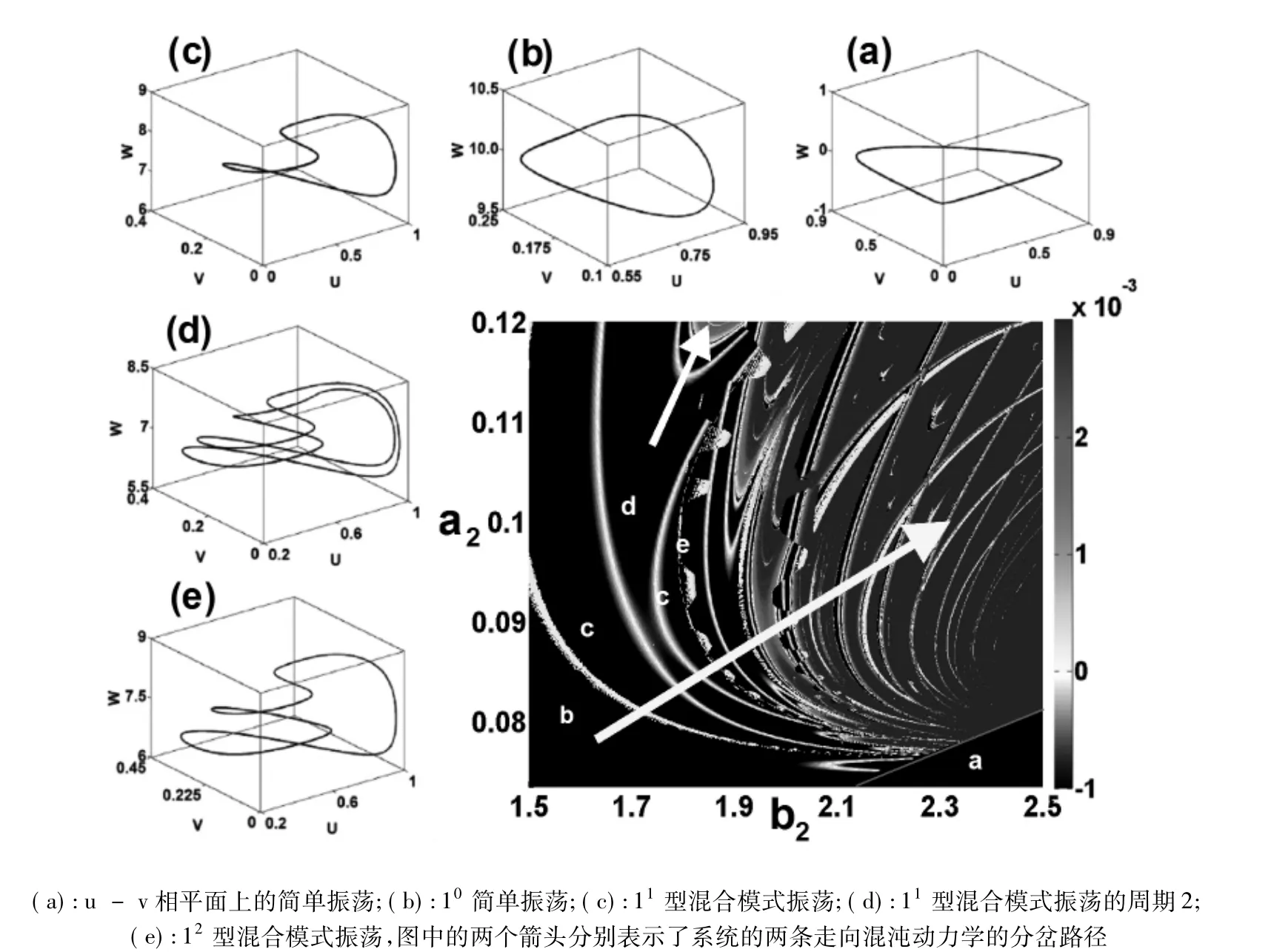
图1 HP均相模型在a2－b2参数空间上的Lyapounov指数相图与典型混合模式振荡行为的吸引子

(1)系统的倍周期分岔线，在图中表现为白色分岔线，系统参数每跨过一次就会发生周期加倍现象或周期倍减现象。

(2)混合模式振荡之间的Fold－Hopf分岔线，在相图内表现为黄色线，系统每经过一次黄线，其对应的混合模式振荡中的小峰就增加一个，即对应着1n－1到1n型混合模式振荡的演化。

同时，在图1中也可以看到HP模型在均相条件下走向混沌动力学的两个路径，白色箭头表示系统经由倍周期分岔走向混沌的方向，而黄色箭头则表示系统经由混合模式振荡的Fold－Hopf分岔走向混沌的路径。本文重点研究了HP模型中混合模式振荡行为的产生机理和演化过程，即黄色箭头方向，对于HP反应－扩散模型的时空斑图模拟工作主要在一维时空系统内进行。

3 时空斑图数值模拟

图2 HP一维反应－扩散系统内的行波与对应的局域振荡形式(a2=0.08)

在对HP反应－扩散进行一维行波的模拟中，系统不同组分的扩散系数分别设定为Du=0、Dv=Dw=0.1，以参数a2，b2为控制参数，其他模拟参数见表1。无特别说明的情况下，在一维系统的行波模拟中，反应时空系统的设置为长度L=3000的一维反应－扩散系统，设置空间步长dx=1.0，时间步长dt=0.01，运用四阶Runge－Kutta算法进行计算。通过对一维系统的一个边界进行激发，而另外一个边界则设置为零流边界可以得到持续传播的行波结构。

在模拟过程中，通过调节b2使得HP系统跨过10型和11型振荡之间的Fold－Hopf分岔(即图1中最下面一条黄色曲线)，在这个过程中可以发现两种不同的行波结构，分别是具有统一振幅的稳定行波结构和具有振幅调制现象的超结构行波。当系统处于远离HP系统的Fold－Hopf分岔线的区域，此时系统内的行波结构与系统本身的均相动力学一一对应，如图2(a)所示，简单的10型振荡对应着具有单一振幅的单峰行波，图2(b)则表示了此时斑图系统内的局域动力学也是10型简单振荡。而在稳定的11型混合模式振荡区域，此时反应－扩散系统所支持的行波是具有双峰结构的稳定行波，其局域动力学行为则表现为稳定的11型混合模式振荡。

在靠近Fold－Hopf分岔曲线的11型混合模式振荡参数区域，虽然在HP均相动力学也表现为稳定的11型混合模式振荡，其对应的反应－扩散行波却在传递过程中发生了调制现象，表现为振幅随着行波的传递发生周期性地变化。如图3(a)所示，此时 a2=0.09，b2=1.60。同时，在整个系统内，具有不同振幅的行波可以在原有的基础行波上形成波包，如图中的红色连线所示，此时反应－扩散系统中产生了新的时空有序结构，表现为在原有行波的基础上形成了新的峰状传输的行波，即超结构行波(Super－traveling wave)。在计算的过程中记录了系统中心位置(x=1500)处的局域振荡行为的时间序列，见图3(b)，不难看出此时系统的局域动力学行为已经不再是均相条件下的稳定11型振荡，而表现为准周期振荡的包络形式，且系统随着时间方向周期性地表现出10和11型振荡模式。

为了进一步了解这种超结构行波在系统内的传播方式，可以记录一维系统内(0，300)区域的时空图，见图3(c)。时空图是研究斑图动力学系统时常用的一种分析方式，它可以清楚地描述系统中各点随着时间和空间的动力学过程。图3(c)中纵坐标表示时间的变化而横坐标则对应着空间的分布，从中也可以观测到的两个时空有序结构，分别以箭头K1和K2表示。其中K1表示系统中的基础行波，其表现为时间上和空间上都是连续的。而K2则对应着振幅调制结构在系统空间内构成的超结构的传播过程，从图中可以看到，沿着K2箭头的方向，具有高振幅的行波波峰(表示为红色区域)虽然并不连续，但是却可以沿着时间和空间构成有序的结构进行传递，从而构成超结构行波。

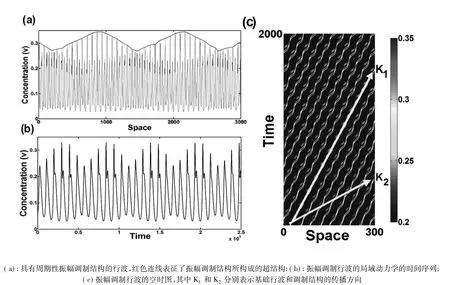
图3 一维HP反应－扩散系内的振幅调制行波(a2=0.09，b2=1.60)

综上所述，通过对HP反应－扩散模型的一维系统的模拟可以发现在一些混合模式振荡区域所对应的行波结构会发生振幅调制，从而构成超结构行波，这种现象出现于两种稳定的振荡模式之间，并表现为多种模式交替出现的振荡行为。虽然此类超结构现象在选择的参数区域可以稳定存在，但是由于行波振幅出现了调制现象，其稳定性如何还需要进一步进行分析。

4 时空斑图的空间递归分析

为了更直接的标度空间中的振幅调制现象对螺旋波结构的稳定性影响，可以选择使用空间递归分析(Spatial Recurrence analysis)对时空斑图的空间稳定性进行分析。

图4是对HP反应－扩散系统的一维行波结构的递归分析结果，其中图4(b)是对稳定的单臂行波的递归分析图，而图4(d)则是对具有振幅调制的超结构行波的递归分析图。通过比较不难看出，稳定的单臂行波的递归图中的结构非常有序，说明此时行波结构是非常稳定的。而由于系统中双峰行波和振幅调制的存在，在递归图图4(d)中的一些区域的斑纹产生了扭曲，其有序性要明显低于图4(a)，这说明此时振幅调制行波的稳定性较差。

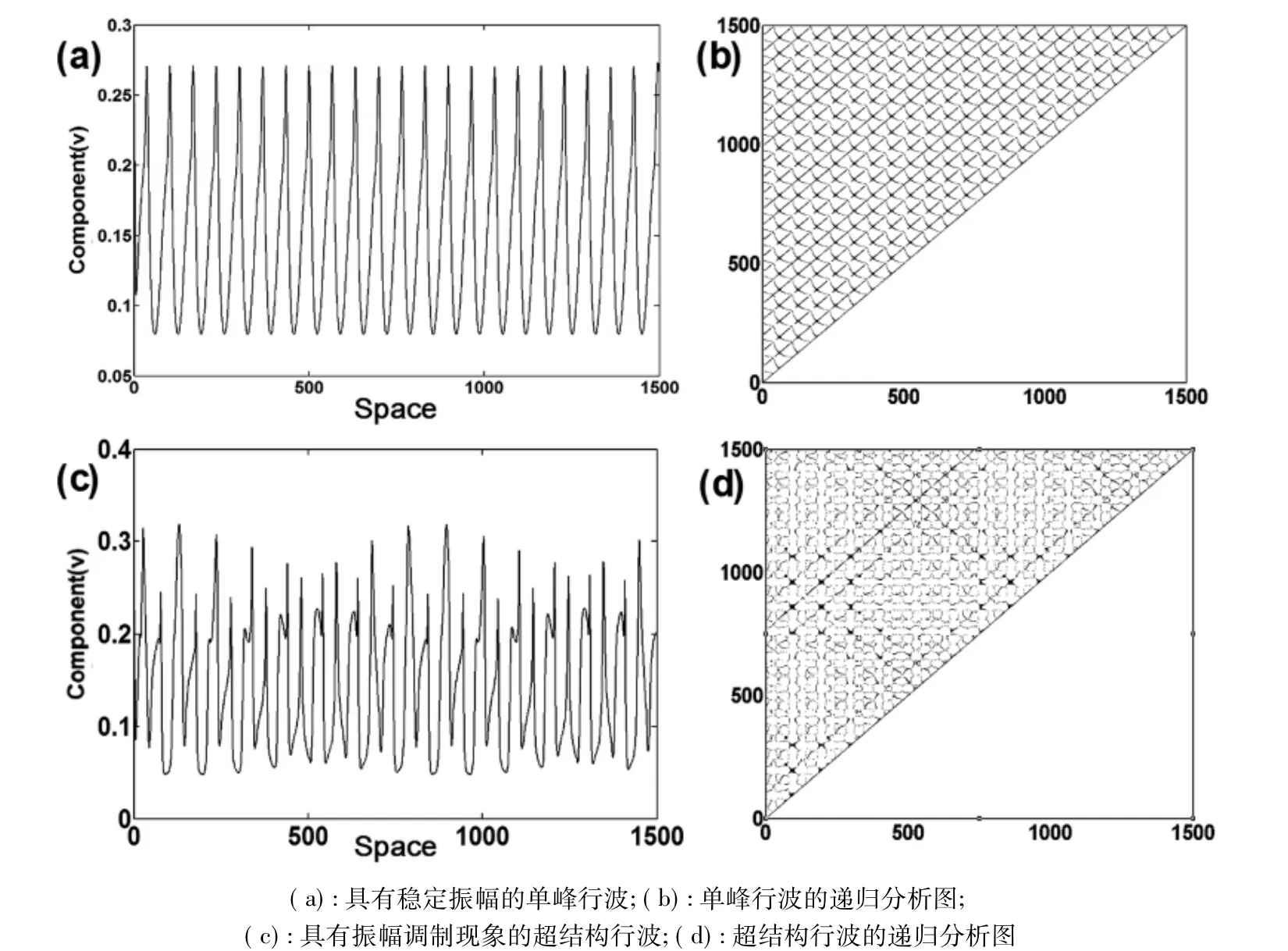
图4 一维HP反应－扩散系统中的行波与对应的递归分析图

5 小结

多反馈系统所具有的混合模式振荡是一种典型复杂非线性动力学行为，其产生根源是反应系统的不同组分构成的多个反馈环之间的相互耦合，从而在一个振荡周期内能表现出不同的振荡模式，如1n型混合模式振荡。而在多反馈反应的时空耦合系统中，扩散的耦合作用在产生时空斑图的同时，其引起空间的不稳定性会影响到斑图的局域动力学行为。扩散诱导的空间不稳定系会改变1n－1到1n(n≥1)混合模式振荡之间的转换过程，产生混合模式振荡的过渡区域(如图3(b)所示)，在此过渡区域内，均相动力学轨道受到扩散的阻尼作用开始收缩并偏离原有的稳定简单振荡轨道，此时局域动力学轨道变现为在10和11的吸引子轨道之间周期性地往返，这种不稳定性会反映在空间结构上，从而形成了具有超结构现象的行波结构。此类超结构现象是在多反馈化学反应－输运系统内具有一定的普适性，但是对于其形成的机理和演化规律的研究目前还是处于理论预测阶段，需要进一步的研究。