分裂四元数矩阵方程AX+XB=C的反Hermite 解

李明照，袁仕芳，田 勇



分裂四元数矩阵方程+=的反Hermite 解

李明照，*袁仕芳，田 勇

（五邑大学数学与计算科学学院，广东，江门 529020）

针对分裂四元数矩阵，和，研究矩阵方程+的反Hermite 解存在的充分必要条件以及有解时的通解表达式。本文利用Kronecker 积，矩阵列拉直算子以及Moore-Penrose 广义逆和分裂四元数矩阵的复表示。

分裂四元数矩阵；矩阵方程；矩阵列拉直算子；Moore-Penrose 广义逆

0 引言

本文引用如下符号：

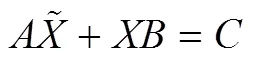
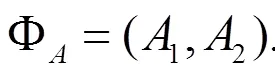
1　几个引理和定义

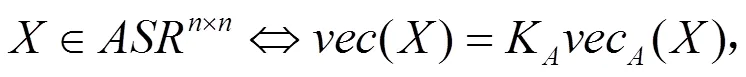
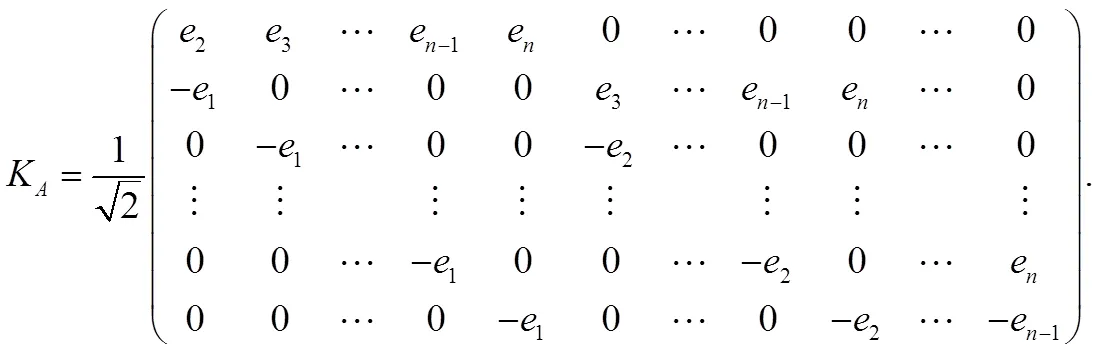
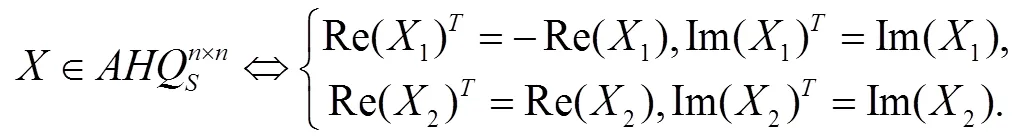
证明

由文献[8]引理 2.6，有以下结果：

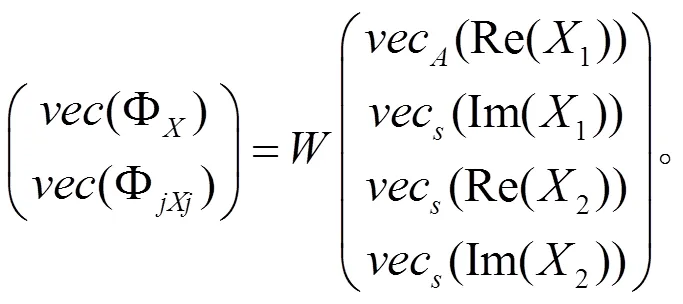
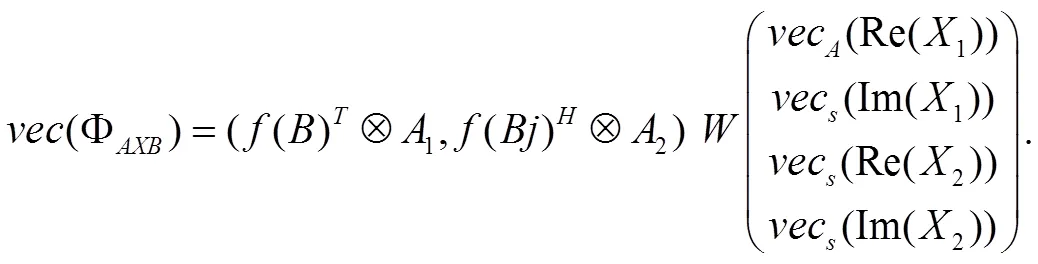
2 矩阵方程(1)的解

基于前面讨论，再求解矩阵方程(1)。设

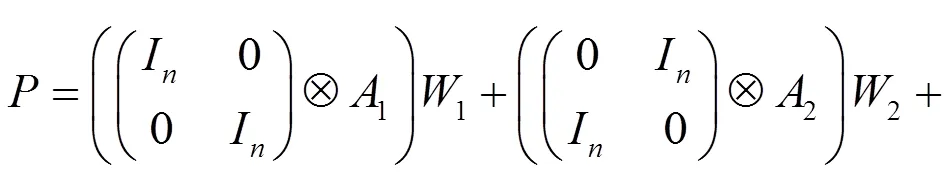
(14)

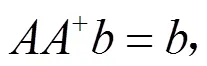
当有解时，它的通解可以表示为

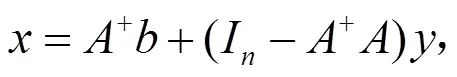
在有解的条件下，记方程(1)的解集合为AH，则

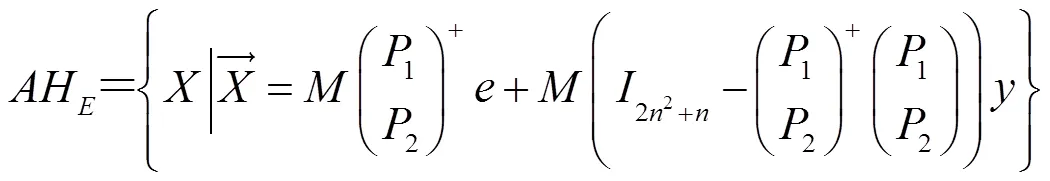
为适当阶数的实向量。进一步，当

证明 矩阵方程(1)可变为

由引理7有

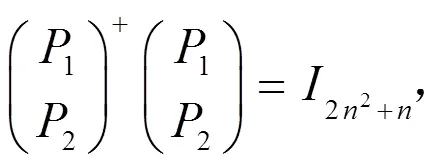
[1] Huang L P. The matrix equation AXB + CXD = E over the quaternion field[J]. Linear Algebra Appl.,1996,234: 197-208.

[2] Yuan S F, Liao A P, Lei Y. Least squares Hermitian solution of the matrix equation (AXB,CXD) = (E,F) with the least norm over the skew field of quaternions[J]. Math. Comput. Model., 2008,48:91-100.

[3] Yuan S F, Liao A P. Least squares Hermitian solution of the complex matrix equationwith the least norm[J].Journal of the Franklin Institute,2014,351: 4978-4997.

[4] Zhang F, Wei M, Li Y, et al. Special least squares solutions of the quaternion matrix equation AXB + CXD = E[J]. Comput. Math. Applic.,2016,72(5):1426-1435.

[5] Alagöz Y, Oral K H, Yüce S. Split quaternion matrices[J]. Miskolc Mathematical Notes., 2012,13:223-232.

[6] Erdögdu M, Özdemir M. On complex split quaternion matrices[J]. Adv. Appl.Clifford Algebras.,2013,23:625- 638.

[7] Erdögdu M, Özdemir M. Two-sided linear split quaternionic equations with unknowns[J]. Linear Multilinear Algebra., 2015,63 (1):97-106.

[8] Yuan S F, Wang Q W, Yu Y B, et al.On Hermitian solutions of the split quaternion matrix equation AXB+CXD=E[J].Advances in Applied Clifford Algebras., 2017,27:3235-3252.

[9] 茂香,姜同松,张兆忠. 分裂四元数线性方程组的Cramer法则[J].泰山学院学报,2016,38(6):37-41.

[11] 戴华. 矩阵论[M].北京:科学出版社,2001.

ON ANTI-HERMITIAN SOLUTIONS OF THE SPLIT QUATERNION MATRIX EQUATION

LI Ming-zhao，*YUAN Shi-fang，TIAN Yong

(School of Mathematics and Computational Science, Wuyi University, Jiangmen, Guangdong 529020, China)

For split quaternion matrices,,we study the necessary and sufficient condition for anti-Hermitian solutions and the general solution expression to split quaternion matrix equationOur tools are the Kronecker product, vec-operator, Moore-Penrose generalized inverse, and the complex representation matrix of split quaternion matrices.

split quaternion matrices; matrix equation; vec-operator; Moore-Penrose generalized inverse

1674-8085(2018)05-0013-04

O241.2

A

10.3969/j.issn.1674-8085.2018.05.003

2018-07-05；

2018-07-20

广东省自然科学基金项目(2015A030313646)

李明照(1988-)，男，广东新会人，硕士生，主要从事数值代数研究(E-mail:wuyilimingzhao@126.com);

*袁仕芳(1972-)，男，湖南邵阳人，教授，博士，主要从事矩阵论和数值代数研究(E-mail:yuanshifang305@163.com);

田勇(1991-)，男，贵州遵义人，硕士生，主要从事数值代数研究研究(E-mail:zytianyong@163.com).