股指期货对冲策略比较研究

邢春娜

(厦门大学 经济学院，福建 厦门 361005)

一、引 言

套期保值是期货市场的主要功能之一，期货合约常用来降低现货交易的潜在风险，对冲的主要目的是规避那些可能造成收益损失或价格波动的风险。最优对冲比率是期货合约头寸与资产风险敞口的比率，现货头寸通过在期货市场上进行等量且反向的交易进行对冲。如果现货市场价格变动幅度与期货市场相同，那么价格风险可以被完全消除，但这种完美的情况在现实中几乎不可能出现。对冲的主要理论问题之一是确定最优对冲比率,而对冲比率的计算取决于需要最优化的目标函数。目前应用最广泛的是通过最小化投资组合方差得到的最小方差对冲比率(Minimum Variance Hedge Ratio，MVHR)。MVHR易于理解和估计，但忽视了对冲投资组合的预期收益，为此Howard and D'Antonio(1984)[1], Cecchetti et al.(1988)[2], Hsin et al.(1994)[3]相继提出了结合投资组合预期收益和方差的对冲策略，当期货价格服从纯粹鞅过程(期货价格变动的均值为零)时它们等价于MVHR。在效用函数和收益分布形式的特殊假定下，通过预期效用函数最大化也可以计算最优对冲比率[4]；为消除效用函数和收益分布形式上的限制，Shalit and Yitzhaki (1984)[5]引入MEG(Mean Extended-Gini)系数，Shalit(1995)[6]随后指出如果价格服从正态分布，由MEG得到的对冲比率与MVHR相同；基于广义半方差(Generalized Semivariance，GSV)或下偏矩的对冲比率[7-8]也受到了关注，因为GSV测度投资组合风险时强调的是低于目标收益的收益率，这与通常的风险发生状态一致；Lien and Tse(1998)[9]证明了在期货和现货收益服从联合正态分布且期货价格服从纯粹鞅过程的前提下，最小化GSV方法计算出的对冲比率等价于MVHR。此外，Hung et al.(2006)[10]通过最小化投资组合在险价值VaR定义一种对冲比率，但与之前的情况类似，当期货价格服从纯粹鞅过程时，它等价于MVHR。

上述对冲策略关于现货收益所有可能取值采用单一的对冲比率，容易忽略现货价格变动所能提供的风险信息，并且不能满足极端价格出现时的对冲要求。当前一些研究往往倾向于从纵向的时变角度说明对冲比率的变化，忽视了横向的现货已实现收益处于不同分位数水平时对冲比率也会发生改变。本文通过引入分位数对冲策略来体现这一点。与最小方差对冲比率相比，建立在分位数回归基础上的分位数对冲比率的优点在于估计结果关于异常值更为稳健，并且可以反映现货收益的不同取值处，特别是尾部极端值的对冲情况。

股指期货是股票市场的一种风险管理工具。为降低持有股票的风险，投资者可以通过交易股指期货合约来稳定投资组合收益。刘向丽和张雨萌(2012)[11]利用沪深300股指期货和现货1分钟高频数据进行分析发现，期货市场有较强的价格发现功能；方匡南和蔡振忠(2012)[12]选取沪深300股指期货5分钟数据，运用误差修正模型、脉冲响应函数研究我国股指期货长短期的价格发现机制以及不同涨跌幅度下的期现关系；陶利斌等(2014)[13]采用信息份额方法和沪深300股指期现货高频数据考察了股指期货价格，发现能力的变化和影响因素；代军和朱新玲(2014)[14]对沪深300股指期货不同套期保值策略的绩效进行比较分析，并讨论了投资者风险厌恶系数和交易成本对套保模型选择的影响；郑振龙和郑国忠(2015)[15]通过基于小波分析的模型来研究沪深300股指期货对冲比率、对冲效率和对冲期限之间的关系。

由此可见，国内股指期货方面的研究关注较多的是股指期货与现货之间的关系和期货的价格发现能力，关于股指期货对冲策略的分析相对较少。本文利用国内三支股指期货和现货的高频和低频数据实证比较分位数对冲策略和最小方差对冲策略，并讨论对冲比率与现货已实现收益和对冲期限的关系。

二、模型设定

(一) 最小方差对冲比率

设st和ft分别表示时刻t的现货和期货对数价格，相应的对数收益率为:△st=st-st-1，△ft=ft-ft-1,对冲的投资组合收益为:

Rt=△st-h△ft

(1)

t=1,2,…，T0，这里的h是对冲比率。最小方差对冲比率记为hmv，是通过最小化Rt方差得到的：

(2)

将△st关于△ft进行线性回归:

△st=α+β△ft+et

(3)

参数β即为hmv。利用最小二乘法得到参数估计值：

(4)

t=1,2,…,T。当期货和现货收益率的时间序列不平稳时，OLS估计结果偏差较大，如果△st与△ft存在协整关系，可以利用误差修正模型进行估计：令st=a+bft+ut

(5)

β是最小方差对冲比率，m、n分别表示现货和期货对数收益率的滞后阶数，通常利用AIC或BIC确定具体值。

(二) 分位数对冲比率

Koenker and Bassett (1978)[16]中提出的分位数回归是一种半参数回归方法，反映了不同分位数水平的因变量条件分布与自变量的关系，并且在异常点处的回归结果是稳健的。假设Y是一个随机变量，分布函数为FY(y)=Pr(Y≤y)。Y的τ分位数记为：

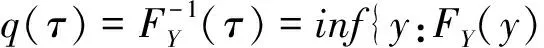
(6)

τ∈[0，1]，FY(q(τ))=τ。ρτ(y)=y(τ-I(y<0))称为损失函数，(6)式可表示为：

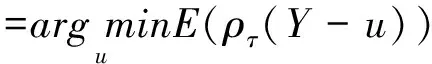
(7)

基于线性模型(3)(误差修正模型(5)有类似表达形式)，△st关于△ft的条件τ分位数记为q△st|△ft(τ)=α(τ)+β(τ)△ft。给定△st的分布函数，通过最小化损失函数期望得到参数向量α(τ),β(τ)向量估计值：

(8)

β(τ)是分位数对冲比率(Quantile Hedge Ratio，QHR)hq在τ分位数水平的值，记为hq(τ)=β(τ)。分位数对冲比率最小化了样本中异常点的影响。α,β与各分位数水平参数α(τ)、β(τ)的关系为：

(9)

参数估计值：

(10)

对投资者来说，理想的情况是hmv=β(τ)关于任意的τ∈[0,1]都成立，在这种情况下，无论做多还是做空都不需要考虑已实现的现货价格。

三、实证分析

(一)数据选取与基本统计量

本文选取国内三支股指期货和标的指数：沪深300股指期货(IF)和沪深300指数、上证50股指期货(IH)和上证50指数、中证500股指期货(IC)和中证500指数。数据统计频率为1分钟、15分钟、30分钟、日、周。为保持数据连续性，选取交易量最大的合约为主力合约，以主力合约收盘价构成的连续价格作为股指期货价格；为保证两个市场数据具有可比性，股指期货1分钟数据剔除了上午和下午最后一分钟的交易数据；15分钟数据剔除了9:30之前和15:00之后的数据。表1中是不同数据频率的股指期货与标的指数的样本区间和样本容量。数据来源为Wind数据库。

表2 中是股指期货和标的指数对数收益率的描述性统计量。总体上看，上证50股指期现货数据与沪深300和中证500股指期现货数据差别较大；虽然三支股票指数收益率均值的变动不太明显，但标准差随着对冲期限长度的增加逐渐增大。

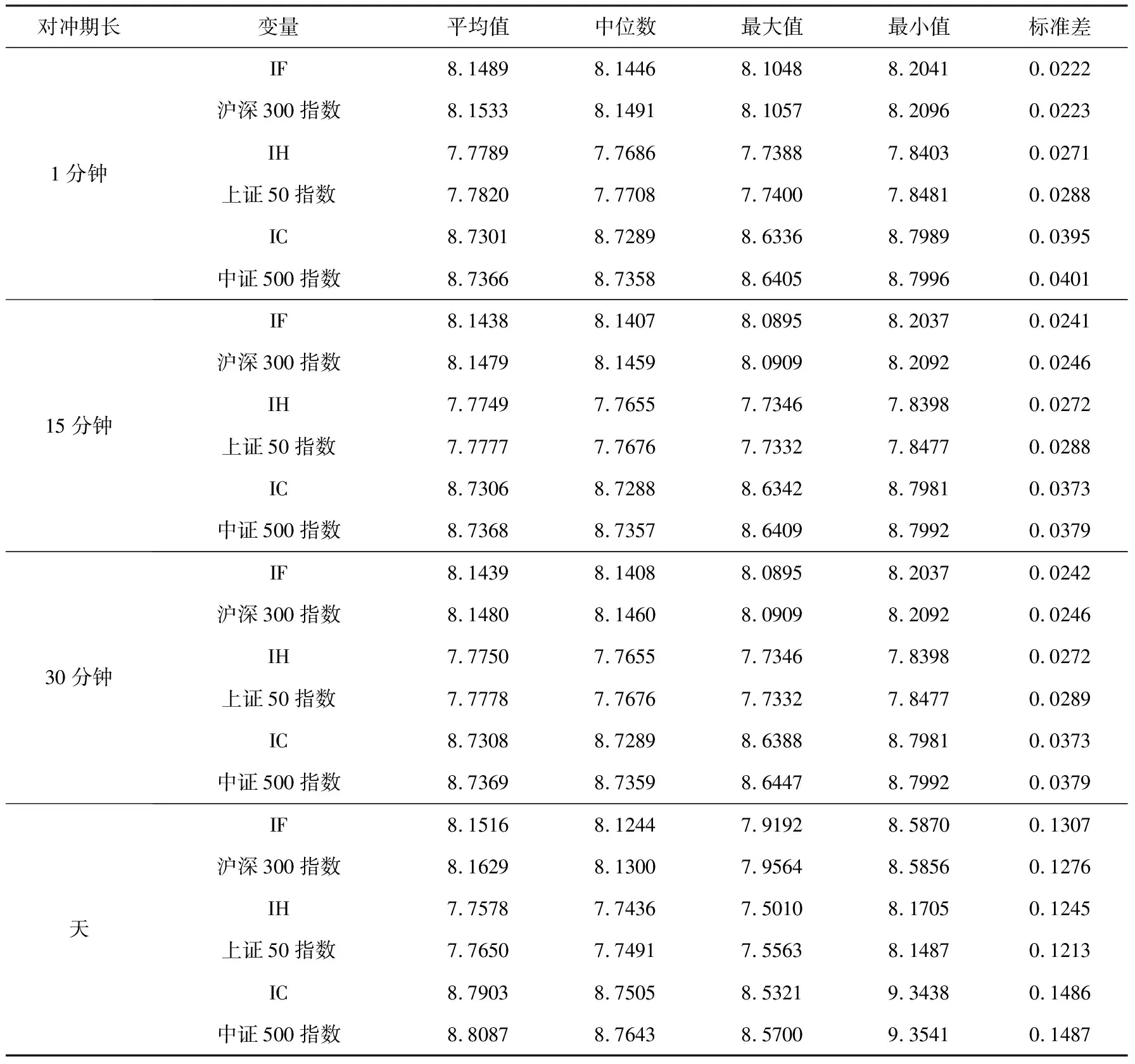
表2 股指期货和标的指数对数收益率基本统计量

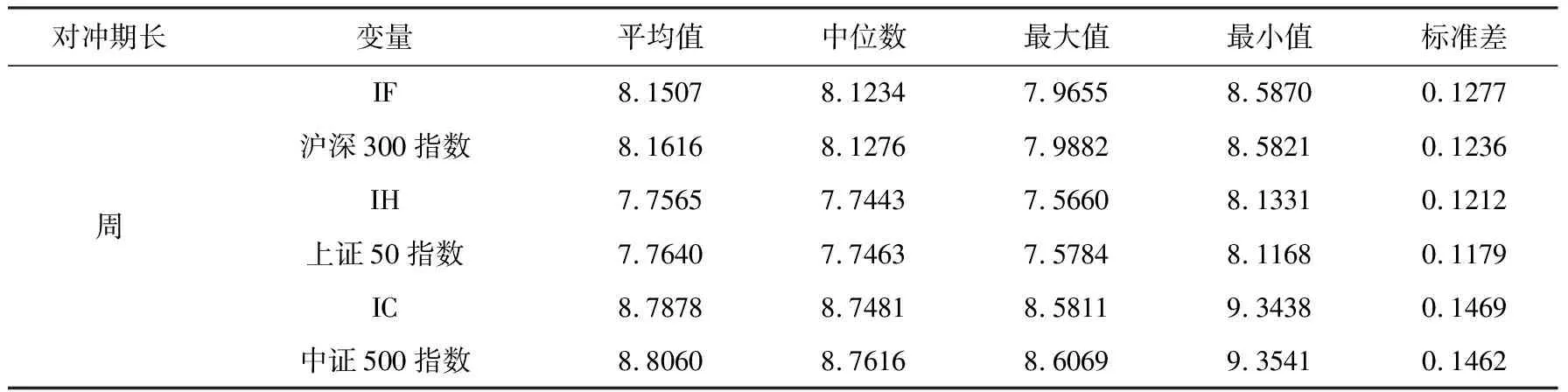
续表2 股指期货和标的指数对数收益率基本统计量

(二)分析过程

为防止虚假回归，首先对各股指期现货收益率数据进行单位根检验，对于不存在单位根的平稳序列，利用(3)进行分析；如果时间序列存在单位根，判断是否为同阶单整，对同阶单整序列进行协整检验；利用Durbin-Watson检验判断具有协整关系的收益率序列是否存在自相关，用AIC、BIC方法确定滞后阶数，并通过误差修正模型(5)进行回归分析。检验结果显示三支股指期货和标的指数时间序列是同阶单整的且存在协整关系，因此利用误差修正模型计算分位数对冲比率。

我们选取15个分位数水平：0.01、0.02、0.05、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、0.95、0.98、0.99。表3中是最小方差对冲比率hmv和分位数对冲比率的估计结果。不管是利用高频数据还是日、周数据，三支股指期货的最小方差对冲比率都随着对冲期限长度的增加而增大；上证50股指期货的hmv在各个期限均高于沪深300和中证500股指期货的hmv；具有相同对冲期限的hmv和分位数对冲比率仍有差异，并且极端分位数对冲比率与中间部分分位数对冲比率的差别也较大，这说明对冲比率取决于标的指数的已实现价格。

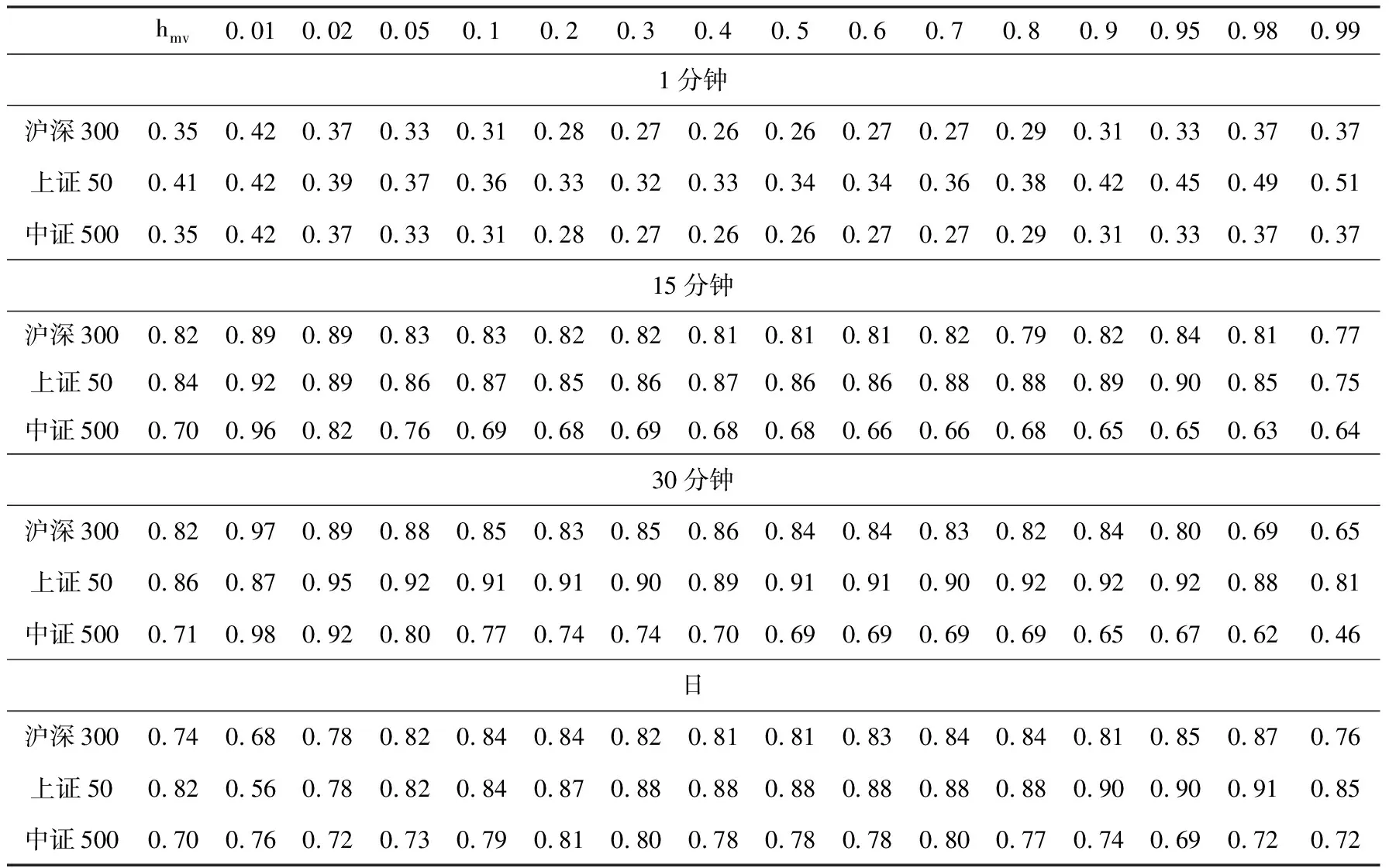
表3 分位数与最小方差对冲比率估计结果

续表3 分位数与最小方差对冲比率估计结果

图1至图5分别是不同对冲期限的分位数与最小方差对冲比率。从图1可以看到，分位数对冲比率呈现U型趋势，中间小两头大，说明当现货收益在中间分位数实现时，采用最小方差对冲比率会对冲过度，而在极端分位数(比如1%、99%)实现时又出现对冲不足；利用15分钟和30分钟数据得到的最小方差对冲比率与中间分位数对冲比率比较接近，但仍无法反映极端情况下的真实对冲比率。在图4和图5中，曲线呈现不明显的倒U趋势，中证500指数的分位数对冲比率波动比较剧烈。

与Lien et al.(2015)[17]中关于发达经济体金融市场股指期货对冲比率的研究结论不同，利用国内股指期现货日数据得到的最小方差对冲比率有效性并不高。为了更好地说明分位数与最小方差对冲比率的区别，我们利用Bootstrap方法检验两者之间差异的显著性，结果整理见表4。从表4可以看出，1分钟高频数据的分位数对冲比率与最小方差对冲比率的差别都比较明显，但15分钟和30分钟数据的结论表明差异不总显著；日数据的分析结果显示在10%以上的分位数水平，分位数与最小方差对冲比率差异较为明显，但周数据的结论显示两者差别不大。

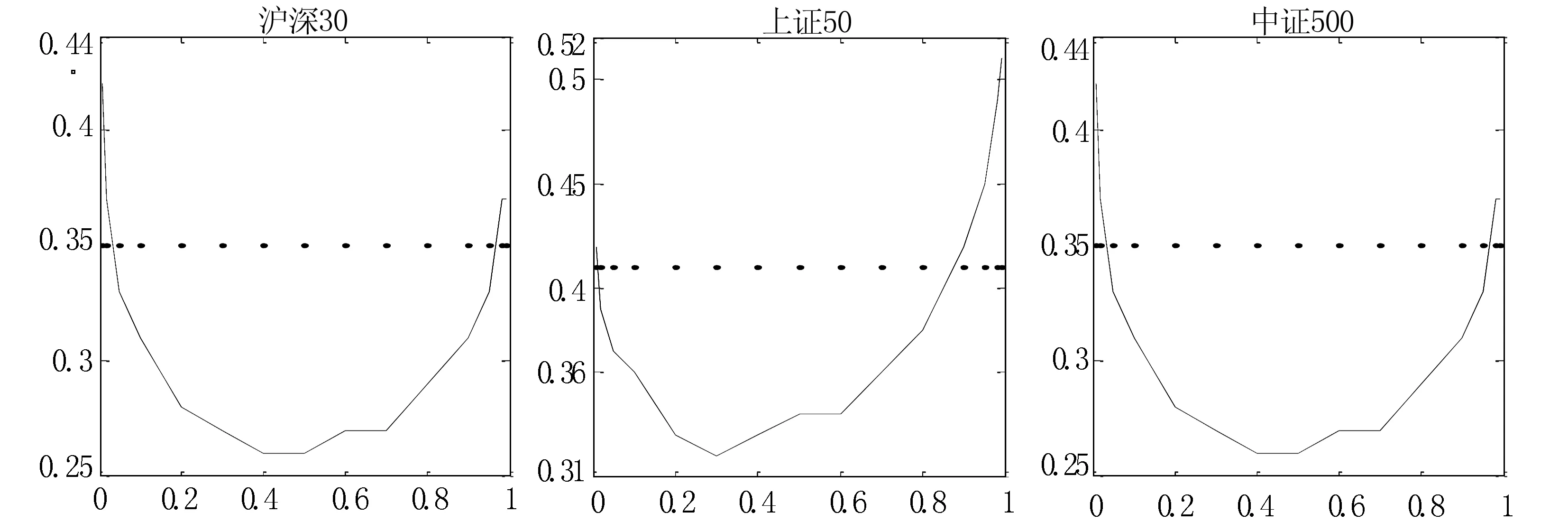
图1 分位数与最小方差对冲比率估计结果：1分钟数据

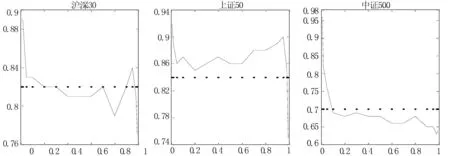
图2 分位数与最小方差对冲比率估计结果：15分钟数据

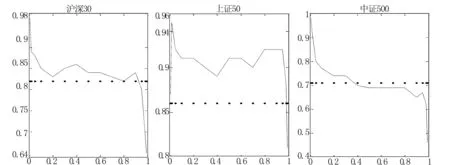
图3 分位数与最小方差对冲比率估计结果：30分钟数据

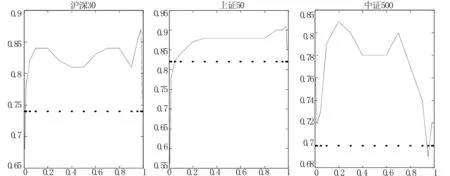
图4 分位数与最小方差对冲比率估计结果：日数据

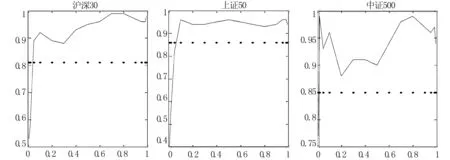
图5 分位数与最小方差对冲比率估计结果：周数据

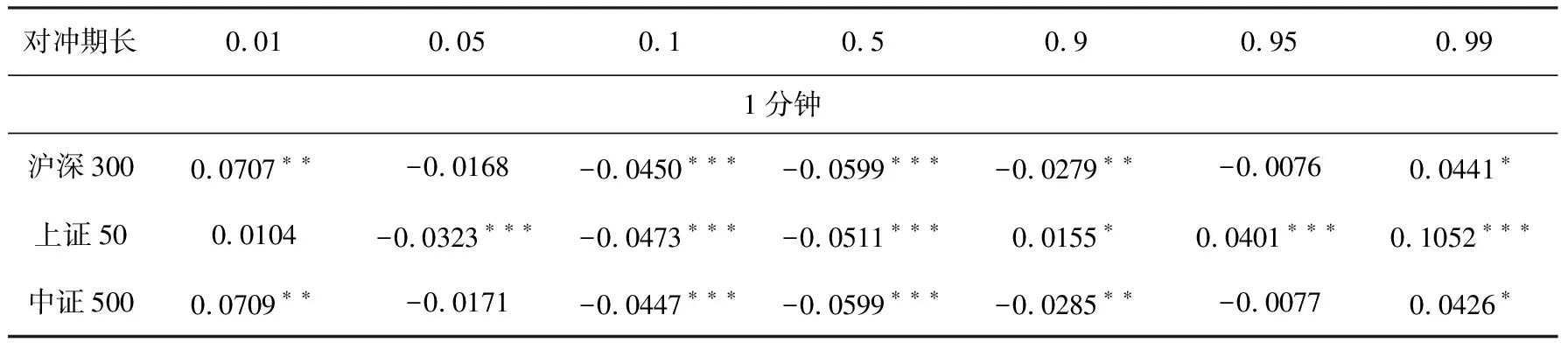
对冲期长0.010.050.10.50.90.950.991分钟沪深3000.0707∗∗-0.0168 -0.0450∗∗∗-0.0599∗∗∗-0.0279∗∗-0.0076 0.0441∗ 上证500.0104 -0.0323∗∗∗-0.0473∗∗∗-0.0511∗∗∗0.0155∗ 0.0401∗∗∗0.1052∗∗∗中证5000.0709∗∗-0.0171 -0.0447∗∗∗-0.0599∗∗∗-0.0285∗∗-0.0077 0.0426∗

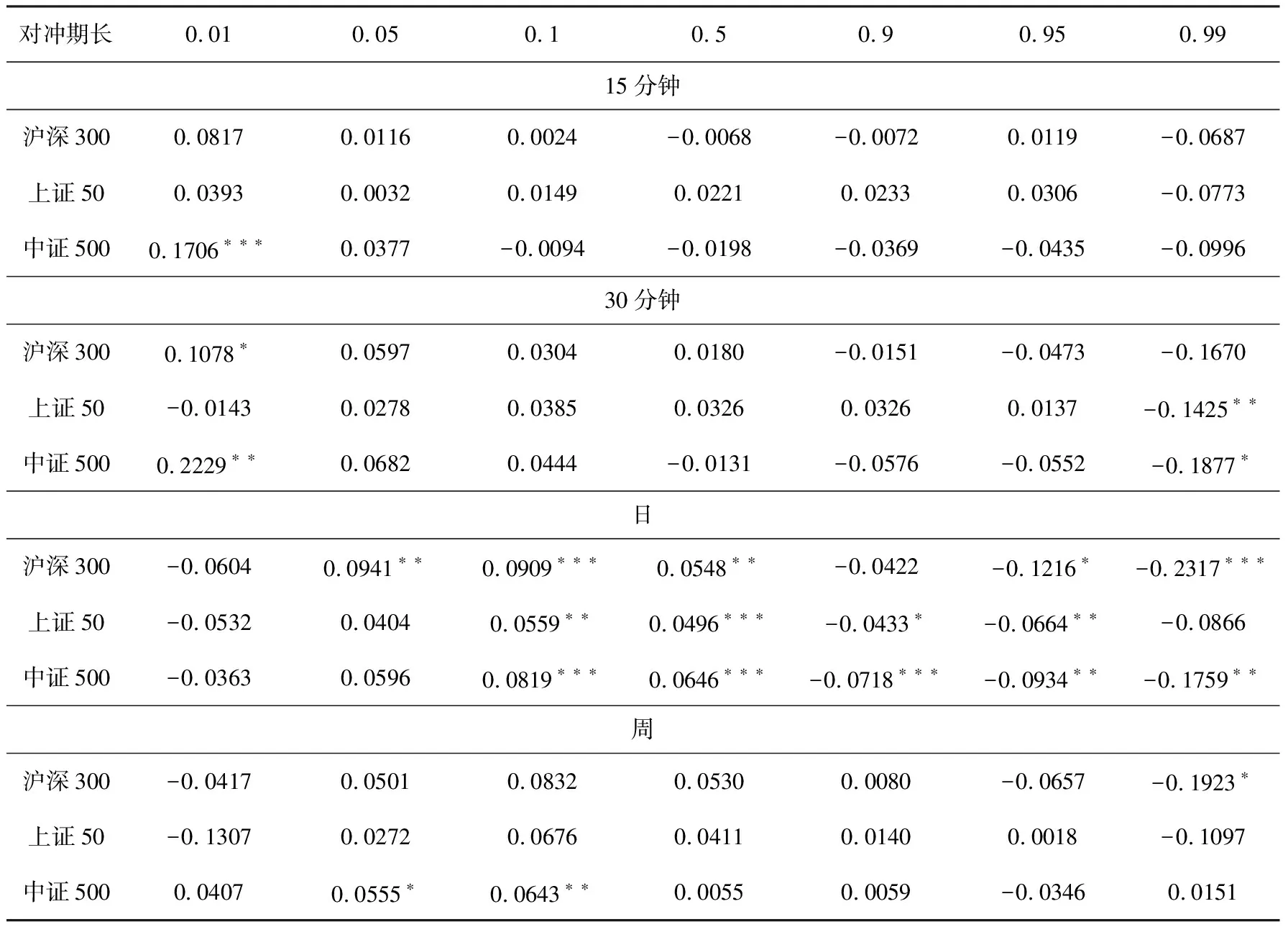
续表4 分位数与最小方差对冲比率之间差异的Bootstrap检验结果

注:*、**、***分别表示在 10% 、5% 和 1% 水平上显著.

四、结论与启示

本文利用国内三支股指期货和标的指数的1分钟、15分钟、30分钟、日和周数据，在误差修正模型基础上估计分位数对冲比率，并与最小方差对冲比率进行比较，主要研究结论有：

1. 使用1分钟高频数据得到的分位数对冲比率与最小方差对冲比率有明显差别，三支股指的分位数对冲比率都呈现U型分布，中间值小、两边值大，说明当现货收益在尾部极端值实现时最小方差对冲策略容易对冲不足，在中间分位数实现时容易对冲过度，因此不能进行有效对冲；

2. 利用日数据分析的结果显示，分位数对冲比率分布具有不明显的倒U型特征，当现货收益处于10%以上分位数水平时，分位数与最小方差对冲比率之间的差异显著;

3. 15分钟、30分钟高频数据和周数据的Bootstrap检验结果显示，分位数对冲比率与最小方差对冲比率的差别并不明显。

本文的研究结论说明，对冲比率的大小取决于标的指数已实现收益，单一取值的对冲比率不足以体现股指价格变化所带来的对冲策略改变，分位数对冲比率随标的指数收益分布的变化而变化，因此能够实现比最小方差对冲策略更高效的对冲。最小方差对冲比率的有效性与对冲期限长度有关，期限越长，有效性越高，这可能与期货价格关于股指价格变动的反应速度有关系。利用1分钟高频数据进行对冲时，股指期货价格都没有根据标的指数价格变动做出及时调整，三支股指期货的分位数对冲比率估计结果在分布上比较相似，随着对冲期限长度的增加，股指期货价格有充分的时间调整以反映现货价格变化，两种方法对冲结果之间差异的显著性降低。