规则波导中正规模式的特性研究

贺昌辉, 黎 静, 朱振波, 洪 亮

(空军预警学院， 湖北 武汉430019)

0 引言

规则波导中，满足边界条件的TE模和TM模有无穷多个，每一个模式均可看成是规则波导的基本模式，它们可以单独或同时存在，这些规则波导的基本模式又称为正规模式或正规波型，研究正规模式的特性具有很重要的意义[1]。如在分析不连续波导时，就常用正规波型的理论将波导横截面上的任意电磁场展开成波导中正规模式的叠加。能作如此处理的前提是正规模式必须具有正交性、完备性和对称性，这就是波导中正规模式的三个重要特性。但在一般的教材中却没有对这三个特性进行详细的分析。

本文详细推导了正规模式的三个重要特性，列举了这些重要特性在将规则色散传输系统等效为均匀传输线及波导模式激励的基本理论分析中的重要应用。

1 正规模式的正交性

由前已知，矩形波导中波动方程的解为简谐函数，圆波导中波动方程的解是贝塞尔函数和简谐函数的乘积，这些函数都是正交的，由这些函数表征的矩形波导和圆波导的正规模式也就具有正交特性[2]。这里用i和j代表两个任意的正规模(i，j为模式编号)，它们的正交性可表述如下：

1.1 不同TE或TM波的纵向场分量正交

∬SEziEzjdS=0

∬SHziHzjdS=0 (i≠j)

(1)

对于该正交性公式(式(1))可以利用电磁理论中的二维标量格林恒等式来加以证明。

二维标量格林第一恒等式为

(2)

式中u、v为两个标量函数,将u、v互相交换后的式子与上式相减，得二维第二恒等式

(3)

现不妨令u=Ezi，v=Ezj，可得

(4)

式中截面S为波导的横截面积，C为波导横截面的周线即边界。在波导的边界上Ez=0，于是上式可写为

(5)

若kci≠kcj，可得∬SEziEzjdS=0，得证。

若令u=Hzi，v=Hzj，同样可证当kci≠kcj时，有

∬SHziHzjdS=0

(6)

当kci=kcj时，由式(5)得不到正交关系，此时可以将这两个简并波型用它们的线性组合代替，形成正交的波型组。

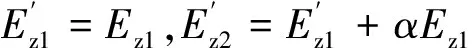
1.2 两个不同的TE波或TM波，或一个TE波和一个TM一个TM波的横向电场分量相互正交

∬SETi·ETjdS=0

∬SHTi·HTjdS=0 (i≠j)

(7)

1.3 两个不同正规模式的传输功率相互正交

传输功率相互正交可表示为

∬SETi×HTj·ndS=0, (i≠j)

(8)

证明：

(9)

式中，Zj为规则波导中第j个正规模式的波阻抗。

正规模式的正交性并不限于理想导体构成的空心波导中的TE和TM模式，对于规则波导中的任意模式，则有以下更一般的正交性公式。

1.4 能量正交性

不管波导壁是理想导体(或良导体)还是非理想导体，均有

(10)

此式可利用洛伦兹互易定理证明。

1.5 功率正交性

(11)

证明：麦克斯韦方程组

▽×H=J+jωD

▽×E=-jωB

(12)

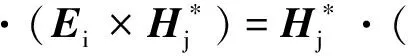
(13)

由式(12)可知

▽×Ei=-jωμHi

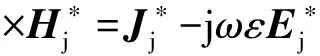
(14)

将式(14)代入式(13)有

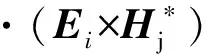
(15)

同理可得

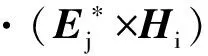
(16)

由式(15)和式(16)可知

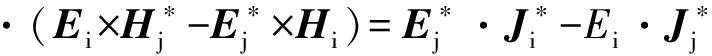
(17)

将上式两端取体积分，并对左端应用散度定理，可得

(18)

因电流源均在空间域V外，即空间域V内无源，右边为0，于是有

(19)

2 正规模式的完备性

当波导中出现任意不均匀体时，在不均匀区，单一模式的场分布不再能满足该处复杂的边界条件，但是我们总可以把这种任意的、复杂的待求场表示成有限个正规模式的叠加，即

(20)

式中ai、bi可用正交关系来确定。当N→∞时，若两者的均方误差趋于零，即

(21)

则正规模形成了一个完备的函数系。因为波导中正规模是满足波动方程和特定边界条件的特征函数，而特征函数系是完备的，所以正规模式构成了完备系。

3 正规模式的对称性

正规模式的电场和磁场对规则波导的纵向坐标(z)具有对称性或反对称性，具体地说，横向电场ET与纵向磁场Hz是坐标z的对称函数，而横向电场HT与纵向磁场Ez是坐标z的反对称函数，即：

(22)

式中，下标“1”代表沿z方向传输的电磁波对应的场量，下标“2”代表沿-z方向传输的电磁波对应的场量。

4 正规模式特性的应用

4.1 将规则色散传输系统等效为均匀传输线

对均匀传输线，线上的电压和电流分别单值地对应于TEM模的横向电场和横向磁场，它们都有确定的含义和确定的值。然而，对像金属波导那样的规则色散传输系统，因为只能传输色散波，传输系统中不存在测量电压和电流的对应端点，因此电压和电流的概念完全失去意义。由此可见，要使传输线理论适合于一切传输系统，必须引进等效参量来代替传输线理论中的电压和电流。这里以单模金属波导的等效为例进行讨论[4]。

设有一个任意截面、无耗传输的单模金属波导,令其横向电磁场为ET(u,v,z)和HT(u,v,z)。为定义单模金属波导某参考面上的等效电压和等效电流，可利用金属波导中(正规)传输模式的以下几个主要特性:

(1)电压和电流分别与ET和HT成正比；

(2)(平均)传输功率等于电压和电流共轭乘积的实部的一半，且在传输若干个波导模式的无耗传输系统中，传输的总功率一定等于各个传输模式的传输功率之和；

(3)行波电压与电流之比等于(选定的等效)特性阻抗ZC(简称等效阻抗)。

根据正规模式的对称性，可写出沿±z方向传输的任意波导模式(包括混合模)的电磁场的一般表达式为

E+(u,v,z)=A+e(u,v)e-jβz+A+ez(u,v)e-jβz

H+(u,v,z)=A+h(u,v)e-jβz+A+hz(u,v)e-jβz

E-(u,v,z)=A-e(u,v)ejβz-A-ez(u,v)ejβz

H-(u,v,z)=-A-h(u,v)ejβz+A-hz(u,v)ejβz

(23)

式中，A+、A-是波导模式的电磁场的振幅；e(u,v)、h(u,v) 和ez(u,v)、hz(u,v)都是二维矢量函数，代表了横向场和纵向场的分布，它们都不是唯一的。因为它们与色散传输系统中的传输模式有关，故称为矢量模式函数。但对于规则单模金属波导而言，波导中的传输模式则是TM或TE模式，此时ez和hz对应为零，这样根据特性1则可将规则单模波导中的横向电磁场表示为以下形式：

ET(u,v,z) =(A+e-jβz+A-ejβz)

(23a)

HT(u,v,z) =h(u,v)(A+e-jβz-A-ejβz)

(23b)

式中，C1=U+/A+=U-/A-，C2=I+/A+=I-/A-，为比例常数(实数)。由于横向电场ET和和横向磁场HT与模式的波阻抗Zw(即ZTM或ZTE)相联系，因此对沿+z方向传输的单向电磁波，e(u,v)和h(u,v) 可按以下关系选取：

(25)

当然，由于e(u,v)和h(u,v)不是唯一的，因此上式中的Zw一般应选定为波导的等效(特性)阻抗。

根据式(23)，即可定义一维标量复函数U(z)和I(z)分别为

U(z)=U+e-jβz+U-ejβz

(26a)

I(z)=I+e-jβz-I-ejβz

(26b)

U(z)和I(z)分别为反映了横向电磁场的导波沿传播方向的变化规律，又因为它们也与传输模式有关，因此称为金属波导中传输模式的等效电压和等效电流(简称为模式电压、模式电流或等效电压、等效电流,或更简称为电压、电流)。

根据特性2可推导出

(27)

根据特性3,假定选定的特性阻抗为ZC，有

C1/C2=ZC

(28)

由此可见，只要用单模金属波导的等效电压和等效电流代替均匀传输线上的电压和电流，则可将单模金属波导等效为均匀传输线。

4.2 用于波导模式激励的基本理论分析

《微波技术与天线》教材中只介绍了金属波导中的模式转换(即金属波导的激励和耦合)，但并未对金属波导的激励和耦合问题作必要的理论分析。下面就利用正规模式的特性来分析金属波导中电流源、磁流源和小孔激励的基本理论。

如图1所示，在无限长金属波导中z1和z2处的两个横截面之间存在(体)电流源J。假设波导中由电流源J产生沿±z方向传输的电磁波的场分别为E+、H+和E-、H-，则根据正规模式的完备性和式

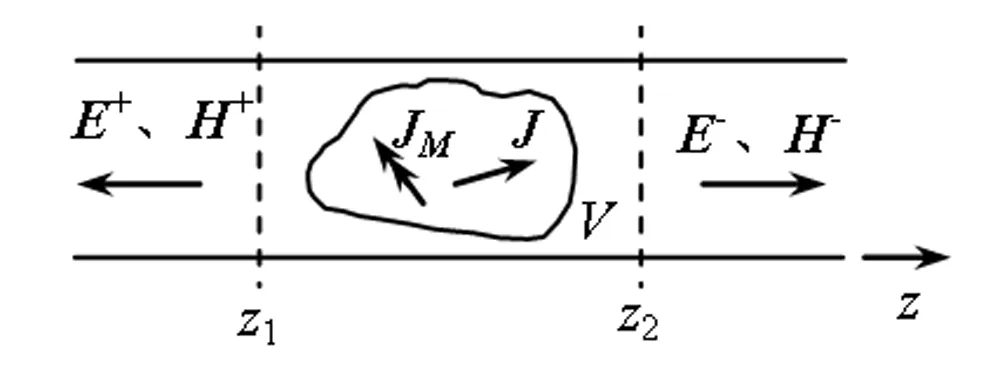
图1 任意电流源或磁流源的模式激励

(24)，可将E+、H+和E-、H-分别表示为

(29a)

(29b)

(29c)

(29d)

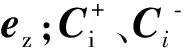
对已知的电流源J，若一体积为V的区域中(体)磁流密度JM1=JM2=0，由互易定理可知

(30)

式中，S为所包围的体积V的封闭面，E1和E2为电流源J1和J2产生的场。于是，取体积V为波导内壁和两个横截面z1及z2所围成的区域，旦令z≥z2或z≤z1区域中的E1=E±，H1=H±，并设E2和H2是沿-z向传输的第i个波导模式的场，即

将它们代入式(30)，并令J1=J、J2=0，可得

(31)

式中，en为体积V的外法向单位矢量。

由于波导内壁表面上切向电场为零，因此关于波导内壁表面的面积分等于零，从而式(31)左端的面积分简化为z1及z2处的两个横截面St上的面积分。又考虑到在波导横截面上波导模式相互正交，即

(32)

利用式(29)及式(32)可将式(31)化简为

(33)

式中St1、St2分别为z1及z2处两个横截面的面积，化简得正向传输电磁波的振幅系数Ai+为

(34)

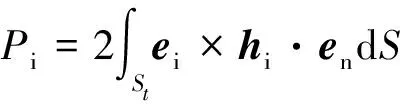
同理可求得

(35)

若金属波导中存在(体)密度为JM的磁流源,由于磁流源同样可在波导中产生正向和反向传输的导波，因此也可采用同上述完全类似的思路导出第i个波导模式正、反向传输波的振幅系数分别为

(36)

上述公式既适用于金属波导中的线电流(探针)激励、电流环(磁环)激励，也适用于金属(薄)壁上的孔缝(小孔)激励。

5 结语

本文推导了规则波导中正规模式的正交性、完备性和对称性三个重要特性，列举了这些重要特性在将规则色散传输系统等效为均匀传输线及波导模式激励的基本理论分析中的重要应用，可见研究规则波导中正规模式的特性在理论与实际中都具有很重要的意义。