复数域傅里叶级数研究性教学改革探索

张 琳， 江 明

(中山大学 电子与信息工程学院， 广东 广州 510006)

0 引言

1998年，美国博耶研究型大学本科生教育委员会的报告《重建本科教育：美国研究性大学发展蓝图》提出：教学应与研究相结合，学生的学习应基于研究，应建立以研究为基础的教学模式[1]。这一报告提出了研究性教学的教学理念，并被贯彻实施于本科教学中。

研究性教学理念起源于20世纪初的中小学教育，随后1910年科普兰(Copeland D.)将其引入哈佛商学院的教堂，采用案例讨论研究讲授工商管理专业知识[2]。1916年杜威提出了“问题教学法”，提倡“从做中学”，论证了教学与科学研究结合的必要性。在此基础上，克伯屈创建了“设计教学法”，“尽可能放手让学生自己管理自己”。1959年和1961年，布鲁纳和施瓦布提出“探究和发现”的方法，倡导学生自己去发现。近年来，各国都在极力发展教育，研究性教学理念及教学方法实施也在不断的得到充实和发展。

笔者对电子与信息领域工程数学课程的研究性教学以及Matlab课程的应用性教学实践进行了探索，分别探究了研究性、应用性教学方法，并以复数域傅里叶级数的教学为例，对其教学目标、教学方案、教学内容进行了设计，还通过Matlab仿真实践进行了验证。此外，本文依据学生的特点，以音乐重构问题为例，详细设计了复数域傅里叶级数的推算及应用的教学实践内容。

1 研究性教学概述

研究性教学强调研究性讲授和研究性学习，在研究性讲授过程中，不仅要解决“该知识点是什么”，还要解决“该知识点是怎么得来的”、“它怎样应用”以及“应用到哪里”的问题；在研究性学习过程中，能够发展学生的认知和创新能力学生的潜能得到充分的发挥，能够深刻认识事理，更加具有主动性。研究性教学具有创造价值：教学过程中，教师和学生的注意力集中，对研究课题的背景知识有深刻认识，容易产生新观点、得出新结论。

研究性讲授与研究性学习本质上就是为了实现学生的发展，培养他们的创造性[3]。

常用的研究性教学方法包括：

(1)案例教学法：教师与学生直接参与，共同对案例或是问题进行讨论的教学方法；

(2)基于问题解决的学习法：由学生提出问题，然后学生通过解决问题获得相应的理解，因此，学生提出问题是这种教学方法的核心；

(3)基于问题的学习法：基于问题的学习法与基于问题解决的学习法不同，前者是在解决一个问题的过程中去学习所需要的新知识，而后者的问题则由教师提供。它强调把学习设置在复杂的、有意义的问题情境中，通过让学习者合作解决真实性问题，来学习隐含于问题背后的科学知识，形成解决问题的技能，并形成自主学习的能力。

本文将采用基于问题的学习教学方法，面向学生这一教学对象，对学生的知识储备及培养需求进行了分析，并选取音乐片段重构为问题对象，讲解了复数域傅里叶级数的数学机理，并启发学生运用复数域傅里叶级数完成音乐片段的重构。

2 复数域傅里叶级数研究性教学设计

依据基于问题的学习的教学方法，我们首先分析了学生的知识储备及培养需求的特点，设计了知识领域、技能及能力领域、情感态度领域的教学目标[4]。在此基础上，我们设计了教学方案、教学目标及授课内容，具体如下所述。

2.1 授课对象分析

复数域傅里叶级数的授课对象是大学二年级上学期的学生，处于基础课与专业课学习的转折阶段。一方面，经过一年级对于“高等数学”、“线性代数”、“大学物理”等课程的学习，学生已具备了微积分计算能力、矩阵及向量组计算能力及物理现象观察与分析能力；另一方面，学生对自己的专业认识尚模糊，学习目标不明确，还未建立数学工具与专业应用之间的关联。为此，依据学生的特点，在复数域傅里叶级数的教学中，将建立数学工具与电子通信领域工程应用的认知和关联，培养学生探索、分析和解决问题的能力。

2.2 教学目标设计

依据授课对象特点，在知识领域、技能及能力领域、情感态度领域，教学目标如表1所示。

表1 复数域傅里叶级数教学目标

2.3 教学方案

基于表1所述的教学目标，我们对复数域傅里叶级数的研究性教学内容进行了设计，教学流程图如图1所示：

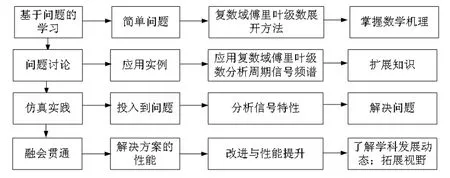
图1复数域傅里叶级数研究性教学流程图

1)音乐频谱分析问题

一段音乐是由一系列具有不同幅度和频率的正弦波叠加而成[5]，借助于Matlab的wavread等函数，可观察到这一段音乐信号可分解为具有不同参数的正弦波分量。这是由于乐器的琴键或是琴弦等发音器件产生的声音与频率点是一一对应的，这就为音乐的人工合成与量化分析提供了可能[5]。

例如，设定频率点和波形，我们可生成如图2(a)所示的音乐片段，为清晰起见，图2(b)给出了放大的波形。该波形可通过应用软件的声音播放函数例如Matlab中的soundsc函数进行播放。进一步，应用复数域傅里叶级数对该音乐片段波形进行分析，即可得到该波形的频谱，如图2(c)所示。

图2(a) Matlab生成的音乐片段波形

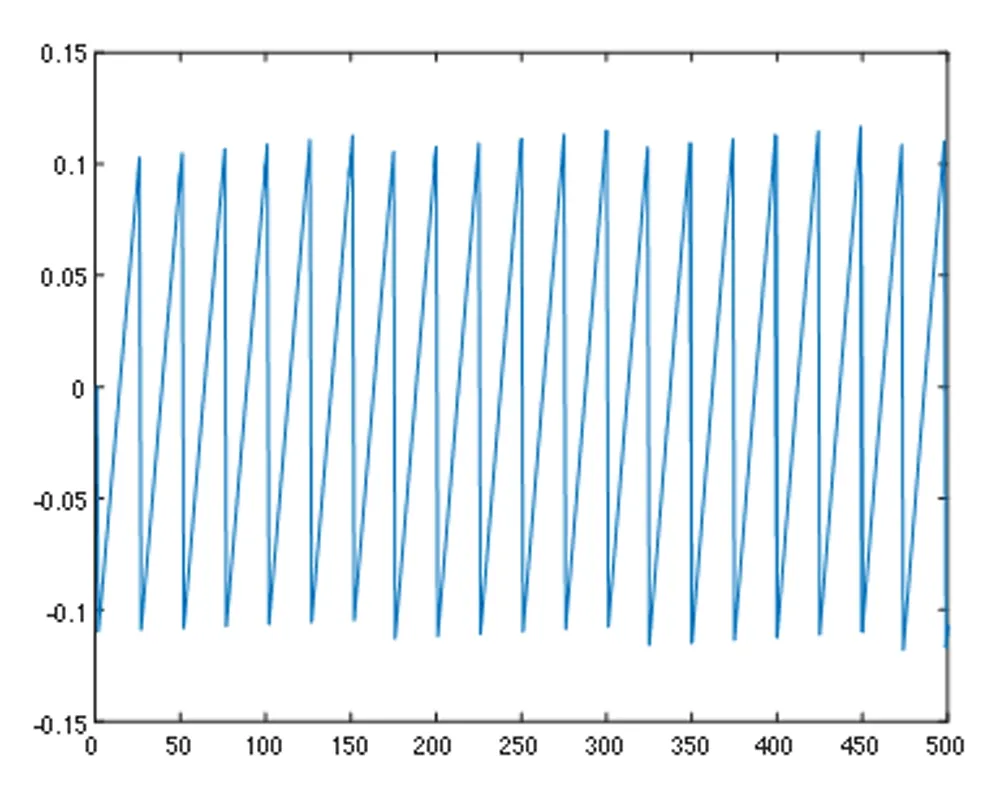
图2(b) [0,500] 对应的音乐片段波形

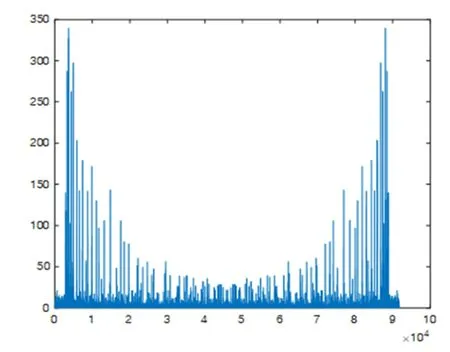
图2(c) 音乐片段的频谱分布图

2)问题讨论

观察图2(a)所示的音乐片段波形，可以看到，该波形具有周期性。对于周期性波形，复数域傅里叶级数可由实数域傅里叶级数推算得到。具体步骤如图3所示：

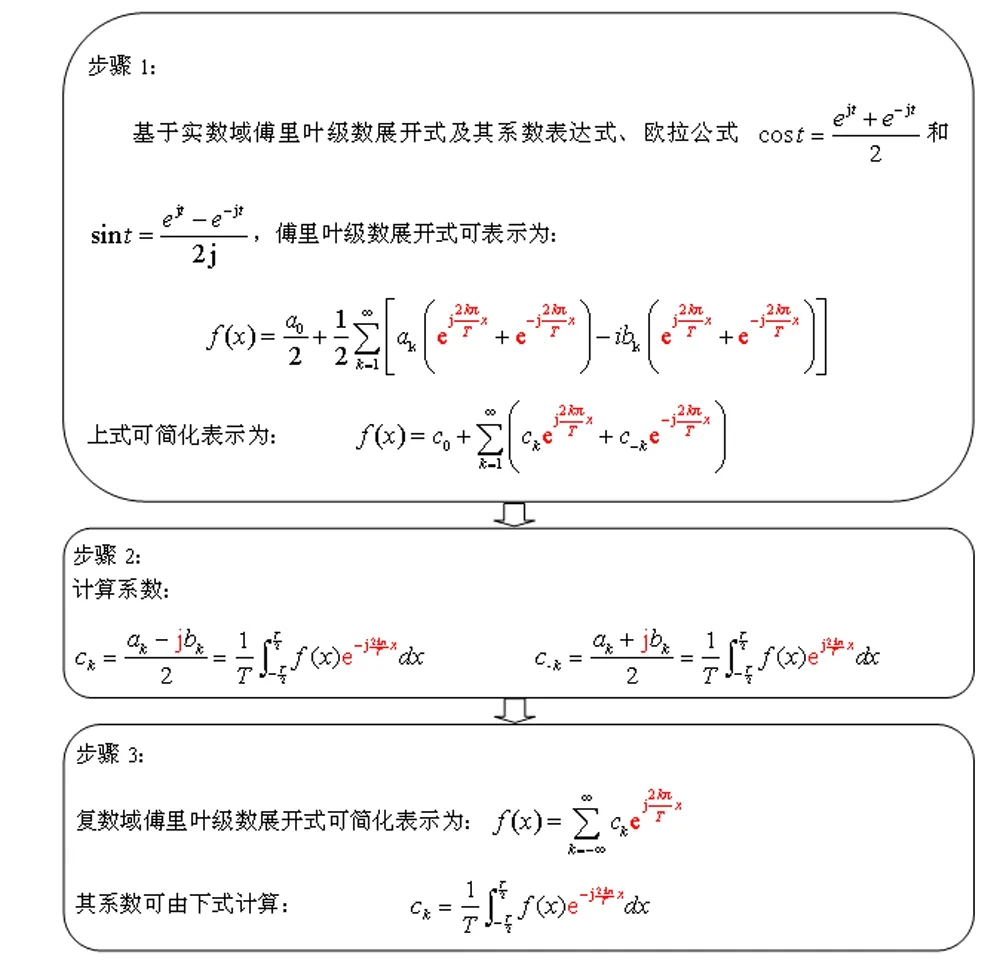
图3 复数域傅里叶级数计算步骤示意图

3)仿真实践

为了验证前述研究性教学的效果，结合Matlab课程的应用性教学实践内容，我们研究了音乐片段及其傅里叶级数展开式的系数模值|ck|的Matlab代码，并在基于Intel i5处理器、8G内存的PC机上进行仿真测试实践[5]。

主要代码如下：

Fs=8192; %样本音符频率

n(1,:)=[5 8 10 5 8 3 5 7 10 13 10 8 1 5 3];

%不同频率点音符的播放顺序

n(2,:)=[0.5 0.5 3 0.5 0.5 3 0.5 0.5 0.5 1 0.5 0.5 1 0.5 3]; %时延数

f=[261.63 277.18 293.66 311.13 329.63

349.23 369.99 392 415.3 440 466.16 493.88 523.25];

%音乐发声频率

ys=0;

%音乐片段函数

for k=1:length(n(1,:));

%生成音乐片段

delay=0.7*n(2,k);

t=linspace(0,delay,round(Fs*delay));

y=sawtooth(2*pi*f(n(1,k))*t);

%生成锯齿波

t=linspace(0,0.7*n(2,k),length(y));

envelope=(t+0.2).*exp(-3*(t+0.2)).*cos(2*t);

%生成信号包络

y=y.*envelope;

ys=cat(2,ys,y);

%生成音乐片段

end

soundsc(ys,Fs);

subplot(2,2,1);

plot(ys);

%绘制音乐片段波形

fft_u=abs(fft(ys)); %计算复数域傅里叶级数展示式系数的模值的绝对值

subplot(2,2,2);

plot(fft_u);

%绘制各频率分量及其幅值

4)物理意义拓展

将复数域傅里叶级数展开式中的系数ck可表示为：ck=rkejθk，其中rk表示ck的模值，θk表示其幅角。代入到傅里叶级数展开式中，可得：

(1)

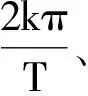
综上所述，以音乐片段为例，我们引入了音乐的频谱分析问题，引导学生思考如何运用复数域傅里叶级数及其频谱分析方法，获得音乐片段的频谱分布。此外，本文借助Matlab软件，对音乐片段的波形及其频谱分布进行了展示，引导学生与机器对话，运用机器理解并掌握数学问题的图形表述方法，并进一步解决频谱分布问题。

3 结语

本文采用基于问题的学习的教学方法，设计了复数域傅里叶级数的研究性教学策略，制订了知识领域、技能及能力领域、情感态度领域的教学目标。在此基础上，以音乐片段的频谱分析为题，设计了复数域傅里叶级数的数学机理推演过程及其物理意义的授课内容，并进行了Matlab课程的教学实践仿真，以提高学生应用数学及计算机工具解决实际问题的能力。我们在教学中实施了该教学方案，取得了较好的教学效果，未来将引入科学合理的评估体系对相关课程教学的效果进行进一步的量化评估。