一个习题“定理”及应用：摩擦力做功的等效性

杨天才

(重庆市第三十七中学校 400084)

推导 如图1，质量为m的物体沿倾角为θ的粗糙斜面AB下滑，相同的物体沿粗糙的水平面OB运动(已知斜面和水平面的摩擦因数处处相同)，两种情况下摩擦力做的功的大小分别为：

结论 若摩擦因数相同，物体沿斜面(AB段或AC段)运动摩擦力做的功等效于物体沿其水平面投影(OB段或OC′段)运动摩擦力做的功.与物体质量、物体所受摩擦力、斜面倾角、位移大小、高度大小、物体的运动状态等其他物理量无关.若带电物体受到恒定向下的电场力作用，该结论仍然成立.

结论的应用

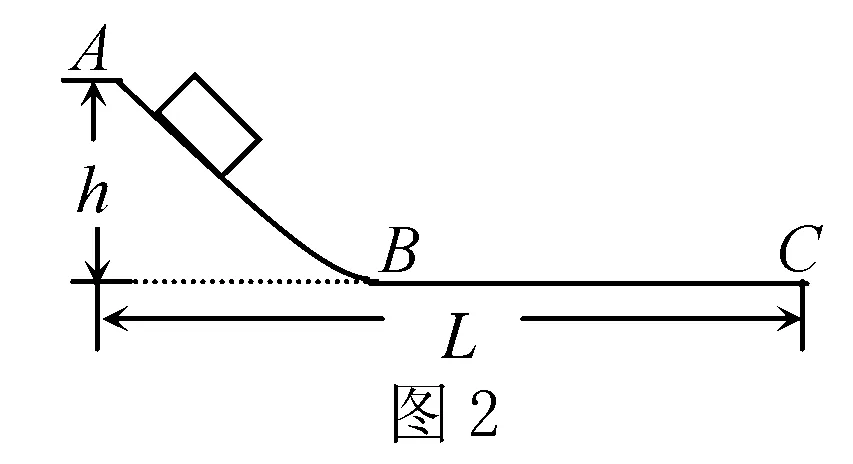
例1 试证明：如图2所示，物体由斜面上高为h的位置滑下来，滑到平面上的另一点停下来，若L是释放点到停止点的水平总距离，则物体与滑动面之间的摩擦因数μ与L，h之间存在关系μ=h/L.

解析 对m，从A→C由动能定理，mgh-WfAB-WfBC=0 ①

由结论化简得：mgh-μmgL=0 ② ∴μ=h/L③

例2 如图3所示，一物块从图中斜面上的A点由静止滑下，又在水平面上滑行一段距离，接着滑上右边斜面并停于B点.若各处的动摩擦因数μ都相等，又测得AB连线与水平面的夹角为θ，试：证明动摩擦因数μ=tanθ.

图4

解析 如图4所示，设AB段的水平长度为x，竖直高度差为h，AC的倾角为α，BD的倾角为β，对m，从A→B由动能定理，mgh-WfAC-WfCD-WfDB=0 ①

例3 如图5所示，DO是水平面，初速为v0的物体从D点出发沿DBA滑动到顶点A时速度刚好为零.如果斜面改为AC，让该物体从D点出发沿DCA滑动到A点且速度刚好为零，则物体具有的初速度.(已知物体与路面之间的动摩擦因数处处相同且不为零.)

A．大于v0B．等于v0

C．小于v0D．取决于斜面的倾角

对m，从D→C→A由动能定理，

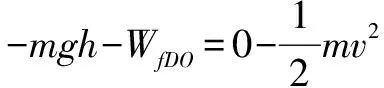
两式相比得v=v0④

例4 (2017年成都一诊)如图6所示，ABCD是固定在地面上，由同种金属细杆制成的正方形框架，框架任意两条边的连接处平滑，A、B、C、D四点在同一竖直面内，BC、CD边与水平面的夹角分别为α、β(α>β)，让套在金属杆上的小环从A点无初速释放.若小环从A经B滑到C点，摩擦力对小环做功为W1，重力的冲量为I1,若小环从A经D滑到C点，摩擦力对小环做功为W2，重力的冲量为I2.则( ).

A．W1>W2B．W1=W2C．I1>I2D．I1=I2

解析 由摩功等效结论，环在AB与CD，AD与BC上运动过程中摩擦力做的功相等，从而环从ABC、ADC运动过程中摩擦力对小环做功相等，选项B正确，由v-t图知，环从ABC路径运动时间较长，重力的冲量较大，如图7，选项C正确.

例5 如图8所示，一个带正电荷的物块m，由静止开始从斜面上A点下滑，滑到水平面BC上的D点停下来．已知物块与斜面及水平面间的动摩擦因数相同，且不计物块经过B处时的机械能损失．先在ABC所在空间加竖直向下的匀强电场，如图9，第二次让物块m从A点由静止开始下滑，结果物块在水平面上的D′点停下来．后又撤去电场，在ABC所在空间加水平向里的匀强磁场，如图10，再次让物块m从A点由静止开始下滑，结果物块沿斜面滑下并在水平面上的D″点停下来．则以下说法中正确的是( ).

图8 图9 图10

A．D′点一定在D点左侧 B．D′点一定与D点重合

C．D″点一定在D点右侧 D．D″点一定与D点重合

解析 由结论知，D′点一定与D点重合；加磁场时，根据动能定理得：mgxABsinθ-μxAB(mgcosθ-qvB)-μxBD(mg-qv′B)=0 不加磁场时，根据动能定理得：mgxABsinθ-μxABmgcosθ-μxBDmg=0,比较两式可得xBD″>xBD，所以D″点一定在D点右侧，故C正确.