混响空时二维特性产生原理及仿真实现

夏 雪 吴 芬

(91388部队41分队1) 湛江 524000) (91917部队2) 延庆 102100)

0 引 言

混响是声呐主动工作方式下的特有干扰，如何抑制混响是声呐信号检测的关键问题.置于载体平台上的声呐基阵接收到的混响，是处于不同方位的大量无规则散射体的后向散射信号在声呐基阵接收点的叠加[1].主动声呐多采用宽波束发射技术，因此，对发射信号进行散射的散射体具有一定的空间分布.当平台运动时，声呐接收到的混响多普勒频率发生扩展，可能使目标回波的频谱与混响的扩展谱混叠在一起，导致常规的检测手段性能下降.

运动平台上的声呐接收到的混响与机载雷达的地杂波具有相似的特性[2-3]，由某散射体反射的混响多普勒频率与入射角之间具有解析的函数关系，即空时二维耦合特性，这使得具有一定运动速度的目标得以与散射元区分开来，可以用空时自适应(STAP)方法进行抑制[4-5].研究混响的空时二维特性对使用空时自适应方法进行声呐信号检测[6-8]具有重要意义.

1 混响空时二维特性及其产生机理

海体中某一散射元与接收阵列的相对位置见图1.

图1 散射元与基阵的几何关系图

图1中标示的黑色粗线为基阵，坐标系原点在基阵相位中心处，载体平台运动方向为X轴正方向，基阵轴向与载体平台运动方向确定的平面为XOZ平面；Y轴垂直于XOZ平面.图中标示的黑色圆点为散射元S；散射元到坐标原点的距离为R；基阵轴向与OS连线夹角为α，称为空间锥角；基阵轴向与OS连线在XOZ平面投影的夹角为φ，称为方位角；基阵轴向与X轴夹角为δ；OS连线与X轴夹角为β；OS连线与其在XOZ平面投影的夹角为θ，称为俯仰角；则经该散射元散射的回波多普勒频率为

fd=fdmcosβ

(1)

cosβ=cos (φ+δ)cosθ

(2)

cosα=cosθcosφ

(3)

将式(2)(3)带入(1)中可得：

fd=fdm(cosθcosφcosδ-cosθsinφsinδ)=

(4)

整理得：

sin2δcos2θ

(5)

式(5)给出了对最大多普勒频率进行归一化后的归一化多普勒频率与α，θ，δ之间的关系，其中，δ是由声呐基阵的布置方式决定的.由于使用的目的和方式不同，基阵的布置方式也是不同的.δ=0°时称为正侧视声呐，典型代表有舷侧阵、拖曳线阵等；δ=90°时称为前视阵声呐，典型代表有球鼻艏、鱼雷制导声呐等；0°<δ<90°时称为非正侧视阵声呐.

1.1 不同声呐布置方式下的混响空时二维分布

当δ=0°时：

(6)

图2为δ=0°时，混响在空时二维平面中的分布

图2 δ=0°时混响的空时分布

由图2可知，δ=0°时的多普勒频率扩展为-fdm～fdm.

当δ=90°时：

(7)

图3 δ=90°时混响的空时分布

由图3可知，δ=90°时的多普勒频率扩展为0～fdm.

当0°<δ<90°时：

(8)

由式(8)可知，当0°<δ<90°时，混响的空时二维分布为一个椭圆，其形状随δ的变化而变化.且由于主动声呐基阵一般处理迎着运动方向接收到的回波信号，实际的空时分布见图4.

图4 δ=45°时混响的空时分布

由图4可知，当0°<δ<90°时，混响在空时二维平面的分布形状为旋转的椭圆形，且旋转角度随δ变化，且其多普勒频率扩展小于2fdm.

以上讨论了不同声呐布置下的混响空时二维分布，当δ=0°时，为斜线分布，其多普勒频率扩展为-fdm～fdm；当δ=90°时，为半圆形分布，其多普勒频率扩展为0～fdm；0°<δ<90°时，为不完整的旋转椭圆形分布，其多普勒频率扩展介于正侧视布置和前视布置之间.然而实际情况中，混响的空时分布不是线状，而是有一定宽度的带状，下面从散射元与基阵俯仰角变化的角度来分析这种展宽产生的机理.

1.2 俯仰角变化对混响空时二维分布的影响

实际接收到的混响是由空间分布的散射体散射产生的.因此，混响的分布形状也受到入射角度变化的影响.

δ=0°时，锥角α一定的情况下，俯仰角θ变化对混响空时分布产生的影响见图5.

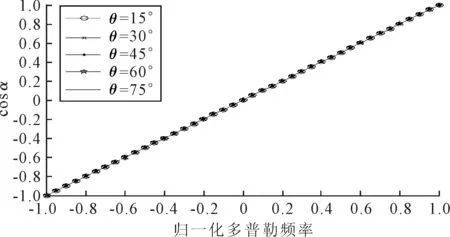
图5 当δ=0°时，θ对混响空时分布的影响

由图5可知，声呐基阵正侧视布置时，当θ变化，混响的空时分布不受影响，扩展仍然为-fdm到fdm.但考虑到实际散射体随机起伏会造成多普勒展宽，实际的混响分布应为斜带状.

当δ=90°，且锥角α一定的情况下，俯仰角θ变化对混响空时分布产生的影响见图6.

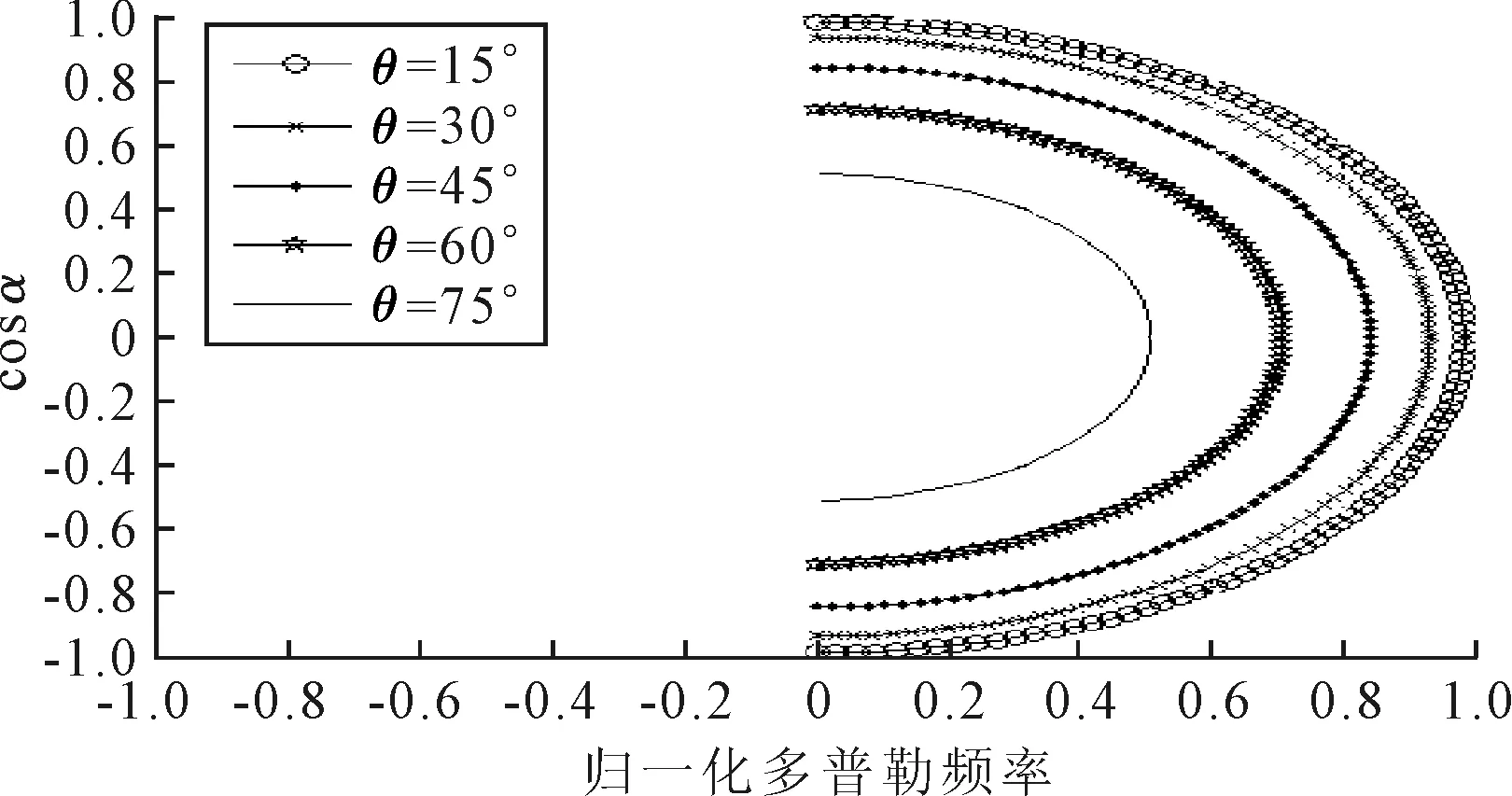
图6 当δ=90°时，θ对混响空时分布的影响

由图6可知，声呐基阵前视布置时，当θ变化，混响的空时分布也随之变化，形成大小不一的圆环，混响的多普勒扩展在0～fdm范围内.这些圆环构成了前视布置下的混响多普勒展宽.

当0°<δ<90°时，且锥角α一定的情况下，俯仰角θ变化对混响空时分布产生的影响见图7.

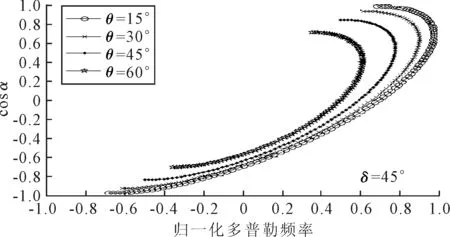
图7 当δ=45°时，θ对混响空时分布的影响

由图7可知，声呐基阵斜视布置时，当θ变化，混响的空时分布也随之变化，多普勒扩展在-fdm～fdm范围内，形成了大小不一的椭圆环，也即俯仰角θ变化使得混响的多普勒扩展发生变化，这些圆环构成了斜视布置下的混响多普勒展宽.

2 混响空时二维特性仿真

2.1 仿真原理

某一散射元与基阵某一阵元的位置关系见图8.

图8 散射元与阵元的位置关系

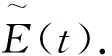
(9)

所有散射元反射的信号叠加在一起即为混响.

(10)

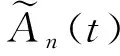
本文采用的混响仿真数据基于以上混响产生机理，并假设：分布于界面及海水中的散射元是随机的，散射特性是均匀的；只考虑散射元的一次散射，信号沿直线传播；在一个脉冲宽度时间内，接收阵元接收到的某一散射元回波的多普勒频移是不随时间变化的.

通过仿真数据，可以进一步分析检验混响的空时二分布，选择采用最小方差(MV)谱来观察混响的空时特性.最小方差谱是通过求解式(11)描述的方程得到的.

(11)

解之得：

(12)

式(11)～(12)中：e(ωt,fd)为空时导向矢量，为空域角频率ωt和时域多普勒频率的Kronecker积.

2.2 混响仿真数据空时二维谱图

仿真试验相关参数：声呐基阵采用阵元数为20的均匀线阵(ULA)，海深100 m，声呐阵距海底43.5 m，黏土底质，风速为6 kn，发射脉冲为频率为3 000 Hz的单频信号，脉宽为0.1 s，平台运动速度为10 kn，采样频率为7 000 Hz，混噪比-20 dB.当声呐基阵轴线方向与运动方向分别成δ=0°，δ=90°，0°<δ<90°时，仿真的混响散射体分布见图9.

图9 声呐基阵分别为正侧视、前视和斜视时的混响散射体分布图

图9中Y轴为运动方向，散射体分布呈U形，随机分布在水体和界面中.

当δ=0°时的仿真混响空时二维MV谱见图10.

图10 δ=0°时混响空时二维最小方差谱

由图10可知，多普勒频率ft随空间锥角的余弦cosα在空时二维平面上呈斜带扩展，与分析结果相符合.但是由于散射体的随机起伏，使得混响的频谱展宽比较大，也即斜带较宽.

当δ=90°时的仿真混响空时二维MV谱见图11.

图11 δ=90°时混响空时二维最小方差谱

当0°<δ<90°时的仿真混响空时二维MV谱见图12.

图12 0°<δ<90°时混响空时二维最小方差谱

由图12可知，混响多普勒频率ft随空间锥角的余弦cosα在空时二维平面上呈带状半椭圆环扩展，与分析相符，且由于散射体随机起伏造成了比较宽的频谱展宽.

3 结 束 语

本文对放置于运动载体平台上的声呐基阵接收到的混响进行了研究.当载体平台运动时，声呐与散射体之间具有相对运动，所以处于不同空间锥角方向上的散射体相对与声呐平台的速度不同，因此从不同方向入射的混响多普勒频率也不同，表现为频率轴上的多普勒扩展，这种扩展就是混响的空时二维耦合特性.进一步研究发现，混响的空时二维耦合特性表现在空间锥角cosα与多普勒频率ft二维平面上具有特定的分布，具体的分布形状取决于声呐基阵轴向与载体平台运动方向的夹角δ.当δ=0°时，混响的空时二维分布是一条斜线；当δ=90°时，混响的空时二维分布是一个圆，考虑到主动声呐一般处理迎着运动方向接收到的回波信号，则其空时二维分布是一个半圆；当0°<δ<90°时，混响的空时二维分布是一个椭圆，同样考虑主动声呐一般处理迎着运动方向接收到的回波信号，则它的混响空时二维分布是一个半椭圆.

而当俯仰角θ变化时，正侧视阵声呐的空时二维分布不随俯仰角变化而变化，前视阵和斜侧视阵声呐的空时二维分布会出现频率的展宽，表现为空时二维分布具有一定的宽度，然而，这种宽度还与散射体的随机起伏等其他不确定因素有关，因此实际的混响空时二维分布是具有一定形状和宽度的不规则带状.

最后利用仿真混响的空时二维谱进行了研究分析，验证了理论分析的结果，为使用空时方法进行混响抑制奠定了理论基础.