不同降雨类型与库水位波动耦合作用下的土质滑坡稳定性分析

2018-12-27秦世伟

中国地质灾害与防治学报 2018年6期

王乐，秦世伟

(上海大学土木工程系，上海 200444)

0 引言

影响库区滑坡稳定性的原因较多，其中降雨与库水位变动是导致滑坡失稳的主要外部因素[1-4]，如1963年的意大利Vajoint边坡，在降雨与库水位变动的情况下，发生了大规模的滑坡失稳事件[5]。库水位骤降与降雨条件下使得滑坡内部的含水量与孔隙水压力变动较大，降低了滑坡土体的强度参数[6-7]，从而导致滑坡灾害的产生，对库岸附近的居民的生命财产安全以及库区的安全运行带来了很大挑战，因此，对于此类问题滑坡的稳定性研究显得十分必要。

库水位与降雨条件下滑坡的渗流特性以及稳定性的研究较多，如方景成等[8]针对库水位骤降速率以及降雨强度两个因素，对边坡稳定性进行了单因素敏感性分析；郭子正等[9]利用灰色模型对三峡库区某堆积滑坡体进行了库水位和降雨联合作用下的安全性评价；唐扬等[10]等基于HYDRUS-1D软件对三舟溪边坡降雨与库水位变动进行了模拟，梁学战等[11]利用Geostudio软件对三峡库区库水位升降作用下滑坡体浸润线变化规律以及滑坡的稳定性；Tang H等[12]对三峡库区黄土坡滑坡在降雨以及库水位变动情况下的变形规律进行了研究；Yin Y P等[13]对三峡库区库水位变动下的滑坡变形特征进行了探讨。但是，对于不同类型降雨叠加库水位骤降条件下滑坡深层浅层滑动的研究还较少，事实上，滑坡在降雨条件下的失稳模式是前期的浅层滑坡，而后产生整体滑动变形，如罗渝等[14]对四种不同类型降雨影响下的边坡深层与浅层滑坡的稳定性进行了研究；王一兆等[15]对降雨入渗条件下边坡深层与浅层的渗流特性以及稳定性进行了探讨，均发现边坡的失稳模式为前期的局部失稳到后期的整体垮塌，鉴于此，有必要对不同类型降雨联合库水位骤降下深层浅层滑坡的渗流特性以及稳定性展开进一步的探讨。

本文以某自拟滑坡为算例，利用加拿大著名岩土有限元计算软件Geo-slope2012，对不同降雨类型联合库水位骤降情况下的滑坡失稳模式，即深层浅层滑坡的渗流特性以及稳定性进行了分析研究，研究成果为相应工况的滑坡稳定性提供了参考。

1 计算原理

1.1 饱和-非饱和渗流原理

以压力水头表示的饱和-非饱和微分方程可以表示为如下形式：

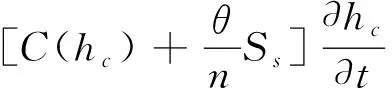
(1)

式中:kij——饱和渗透张量；

kr——相对透水率；

hc——压力水头；

Q——源汇项；

C(hc)——容水度；

θ——与压力水头相关的函数；

n——土体内部的孔隙率；

Ss——单位贮水量。

土水特征曲线是表征土体基质吸力与渗透系数(体积含水量)之前的函数关系的曲线，比较广泛应用于土体非饱和渗流计算的模型是Fredlund&Xing[16]模型，控制方程可以表示为：

(2)

式中：θw——体积含水量；

Cφ——修正函数，本文取为1；

θs——饱和体积含水量；

e——自然对数；

φ——负孔压。

a，m，n为拟合参数，a是体积含水量函数的拐点，其值略大于进气值，单位为kPa，m控制了残余含水量，n控制了体积含水量函数的斜率，表达形式如下：

a=φi

(3)

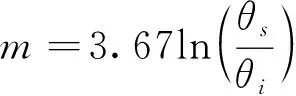
(4)

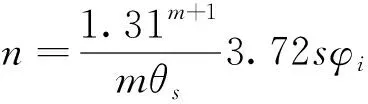
(5)

其中：φi——拐点对应的基质吸力；

s——拐点处的斜率。

根据Fredlund&Xing的体积含水量函数[17]，已知土体的饱和体积含水量θs，便可估算出渗透系数函数：

(6)

其中：kw——负的孔隙水压力所得的渗透系数;

ks——饱和渗透系数;

y——虚拟变量;

i——j到N之间的间距;

j——最小负孔隙水压力;

N——最大负孔隙水压力;

Ψ——对应于第j步的负孔压;

θ0——起始值。

1.2 非饱和抗剪强度理论

非饱和抗剪强度理论采用Fredlund双应力变量公式[17]：

s=c′+σntanφ′+(ua-uw)tanφb

(7)

式中:c′与φ′——有效强度参数；

σn——法向总应力与孔隙气压力的差值；

ua——孔隙空气压力；

uw——孔隙水压力；

φb——表征由负孔隙水压力而提高的强度。

2 计算模型即边界条件

2.1 计算模型

某滑坡体平均坡度约为28°，滑坡体长约为83.5 m，平均厚度为18.2 m，该库区死水位高程为145 m，正常蓄水位高程为175 m，滑坡典型剖面图如图1所示。相应的网格剖分图如图2所示。全局单元尺寸约为6 m，单元类型为四边形单元与三角形单元，整个模型一共剖分为2 564个节点，1 892个单元。为实时监测滑坡不同部位孔压变化，在滑坡体不同位置设置三个监测点，如图1所示，同时，为探究深层浅层滑坡的失稳规律，在模型中设置三个特征滑动面，上部浅层滑动面与下部浅层滑动面为指定的浅层滑动面，而深层滑动面为软件自动搜索的滑动面。

2.2 初始条件以及边界条件

初始条件：以ef边界190 m水头，cb为相应高程水头边界计算所得的稳定渗流场作为各个工况的初始条件。

边界条件：(1)模型ef为零流量边界，abc为水位变动边界，根据Geo-slope2012[17]：cb边界上每一节点的水头值随时间不断变化，软件每运行一步便判断节点水头是否小于节点高程，若条件成立，则该节点的流量Q便被赋予为0；(2)模型dc为降雨入渗的流量边界，当降雨强度大于渗透系数时，入渗强度为土体渗透系数大小，当降雨强度小于入渗强度时，入渗强度为降雨强度；(3)af，de为不透水边界，边界上流量Q被赋予为0。

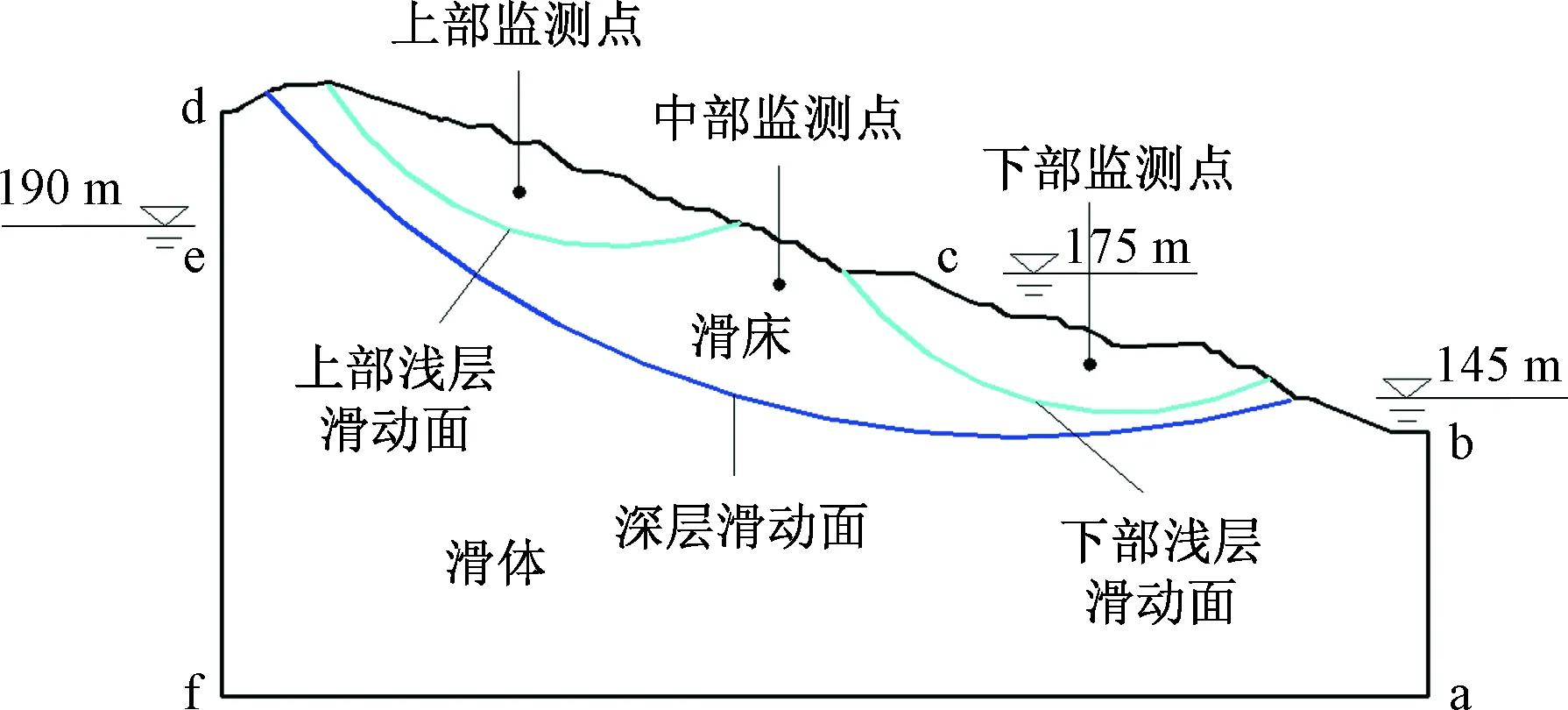
图1 计算模型Fig.1 Calculation model

3 土体参数及计算工况

3.1 土体参数

滑体与滑床的土体参数见表1，非饱和土体积含水量函数曲线根据式(2)～(5)进行拟合，已知参数a，m，n的值，便可由式(2)绘制出体积含水量随基质吸力的变化曲线，见图3(a)，同时，由(2)式得到的体积含水量函数曲线根据式(6)便可绘制出渗透系数曲线，即土体渗透系数随基质吸力的变化曲线，见图3(b)。

表1 材料物理力学参数Table 1 Physical Mechanical Parameters of Materials

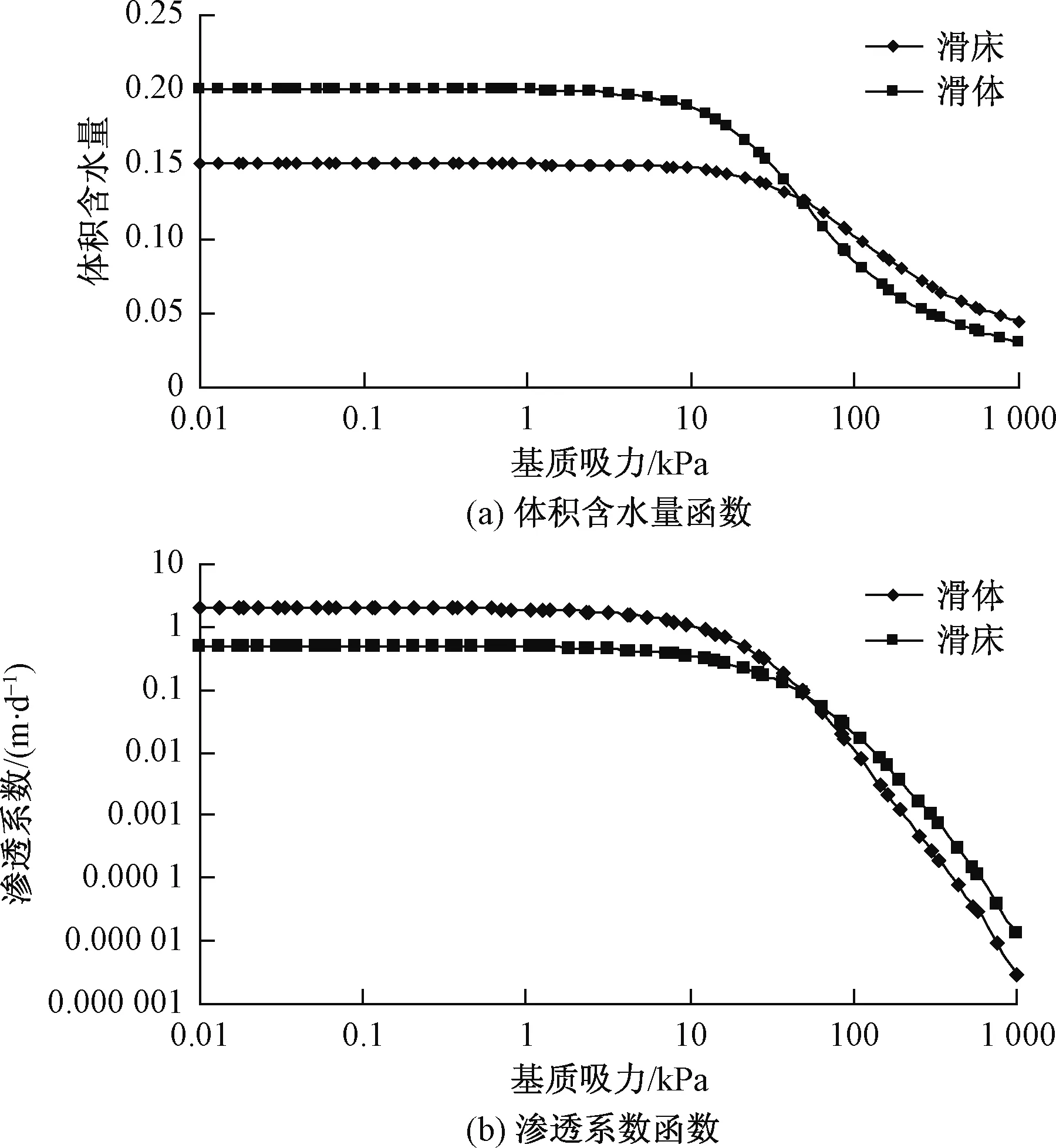
图3 土水特征曲线Fig.3 Soil-water characteristic curve

3.2 计算工况

为研究不同降雨类型对库水位骤降下的深层浅层滑坡失稳规律，本文选取以下三类典型工况：(1)不同库水位下降速率情况下的滑坡渗流特性及浅层滑坡与深层滑坡稳定性分析；(2)静库水位联合不同类型降雨条件滑坡渗流特性以及深层滑坡与浅层滑坡的稳定性分析；(3)库水位骤降联合不同时刻降雨条件下滑坡的渗流特性以及深层与浅层滑坡的稳定性分析。降雨类型根据以往的文献[18-19]，降雨强度根据三峡库区暴雨情况，保持10 d降雨总量一定，选取典型的四种降雨类型-平均型，前峰型，中峰型以及后峰型降雨，降雨时程曲线见图4，相应的计算工况见表2。

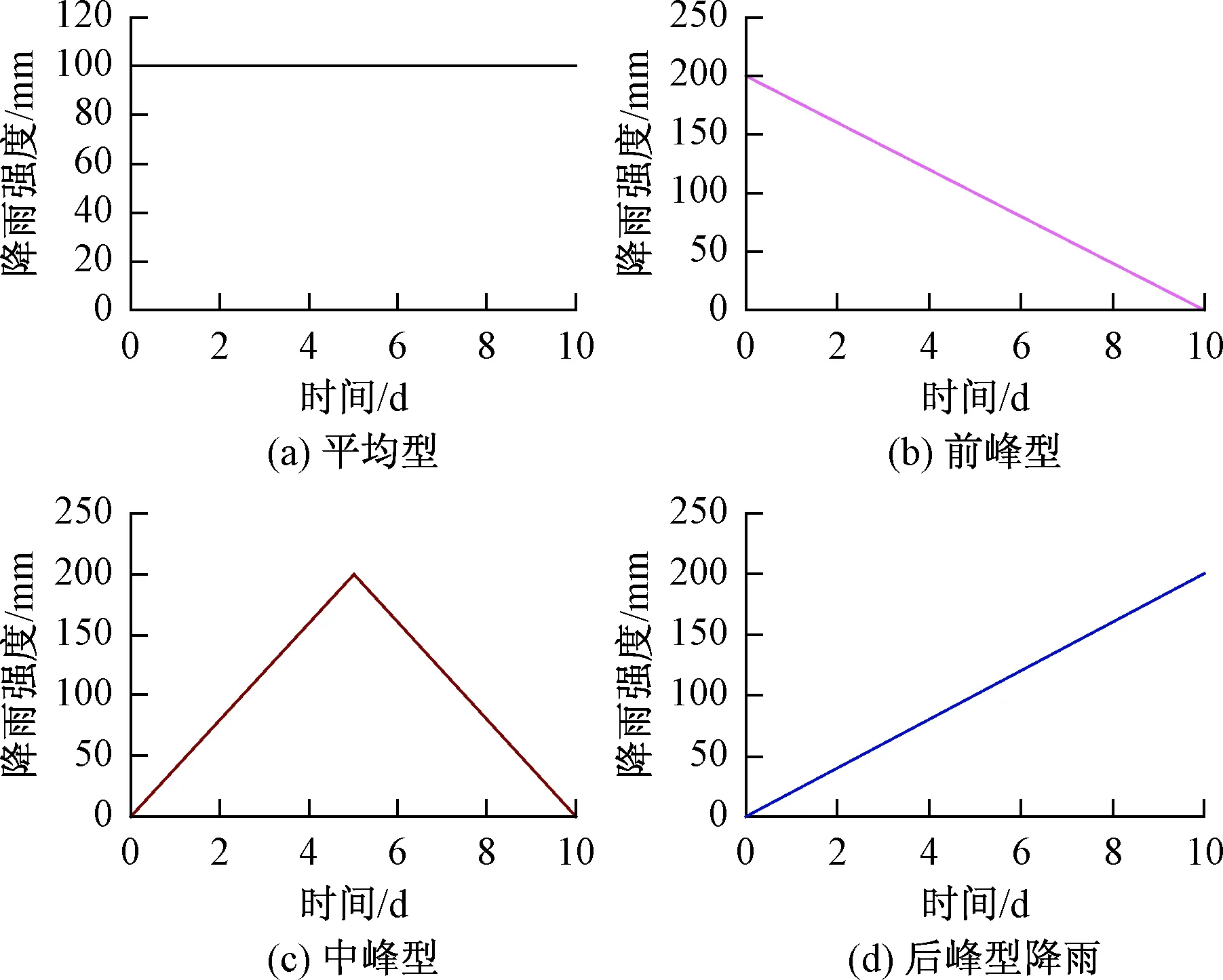
图4 降雨历程曲线Fig. 4 Rainfall history curve

编号计算工况库水位降雨库水位/m下降速度/(m·d-1)降雨类型发生时刻/d工况1不同速率库水位骤降175→1450.51.01.5——工况2静库水位+不同类型降雨1650(1),(2),(3),(4)0～10工况3库水位骤降+不同时刻降雨175→1450.5(1)0～26～812～1418～2024～2630～3236～3842～4448～5054～56

注：(1)，(2)，(3)，(4)分别代表平均型、前峰型、中峰型以及后峰型降雨。

4 计算结果

4.1 库水位骤降工况

库水位从175 m高程下降到145 m高程，骤降速率为0.5 m/d，1 m/d，1.5 m/d情况下，三个测点的孔压变化如图5所示。

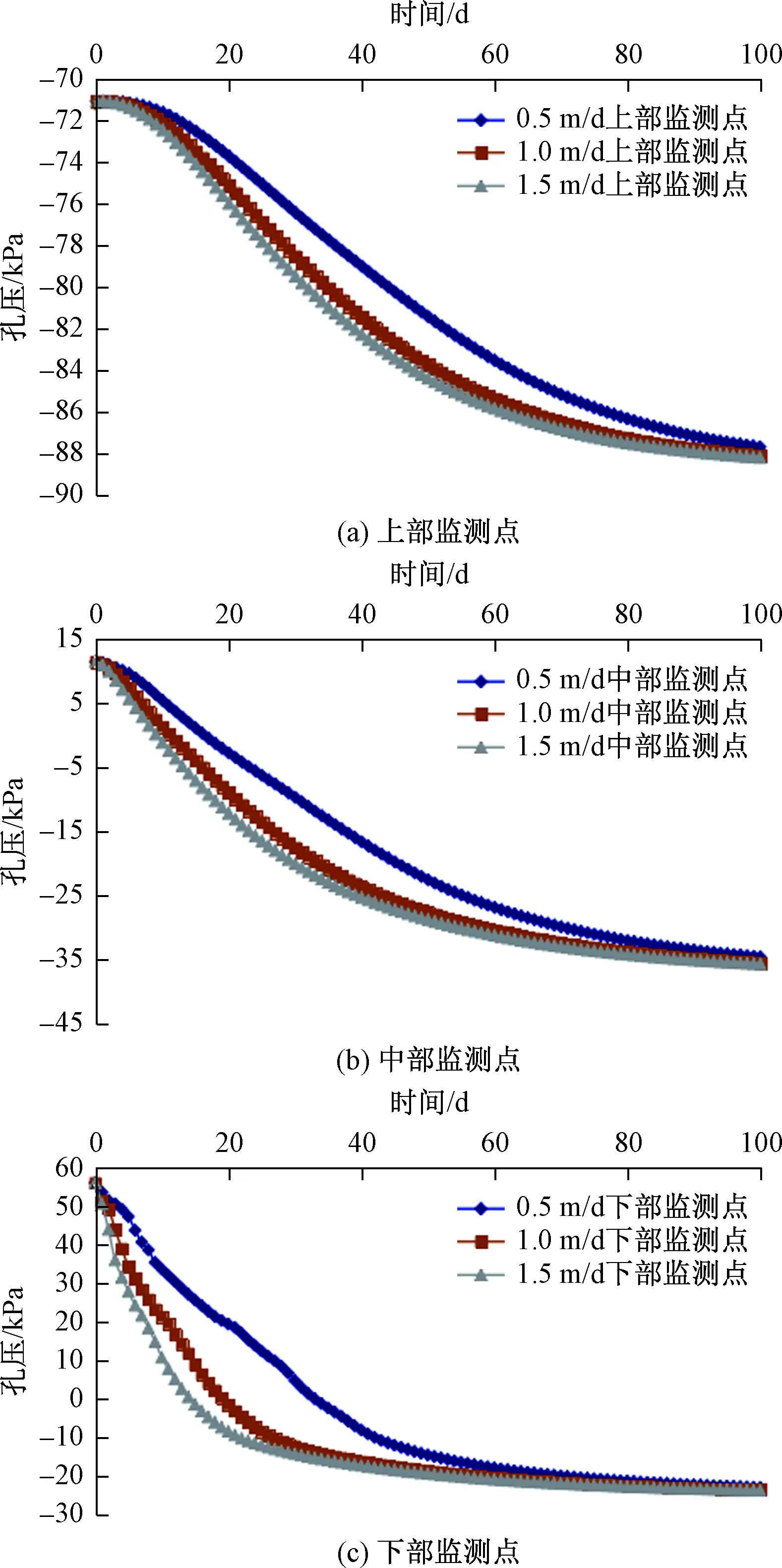
图5 工况1监测点孔压变化Fig.5 Change of pore pressure at monitoring point under calculation condition 1

由图5可见，孔压变化规律总体上是随着库水位下降而逐渐下降，但是不同监测点的孔压变化规律稍有差异，上部监测点距离库岸的距离最远，孔压在10 d前几乎不变，而在10 d之后开始下降，中部监测点距离库岸较近，孔压在前3 d几乎不变，而在3 d之后开始下降。下部监测点离库岸最近，在库水位骤降开始便随时间呈现下降的趋势，说明随着滑坡内部监测点距离库岸的距离增加，滑坡内部的“延迟”效应也越来越明显。同时，库水位骤降情况下不同滑坡体内部的孔压变幅也随监测点距库岸的距离的不同而不同，如上部监测点变幅为15 kPa，中部监测点孔压变幅为46 kPa,而下部监测点孔压变幅最大为77 kPa，可见随着边坡体内的监测点距库岸越远，孔压的变幅也越小。同一监测点不同库水位下降速率下孔压变化也稍有不同，库水位下降速率越大，孔压在前期下降速率越大，表现为图5中曲线中斜率较大的情况，在库水位下降完成后期，监测点的孔压趋于一致，即库水位下降速率影响了监测点孔压的变化速度，而对监测点孔压最终的状态无影响。

不同库水位下降速率下的深层浅层稳定系数如图6所示。

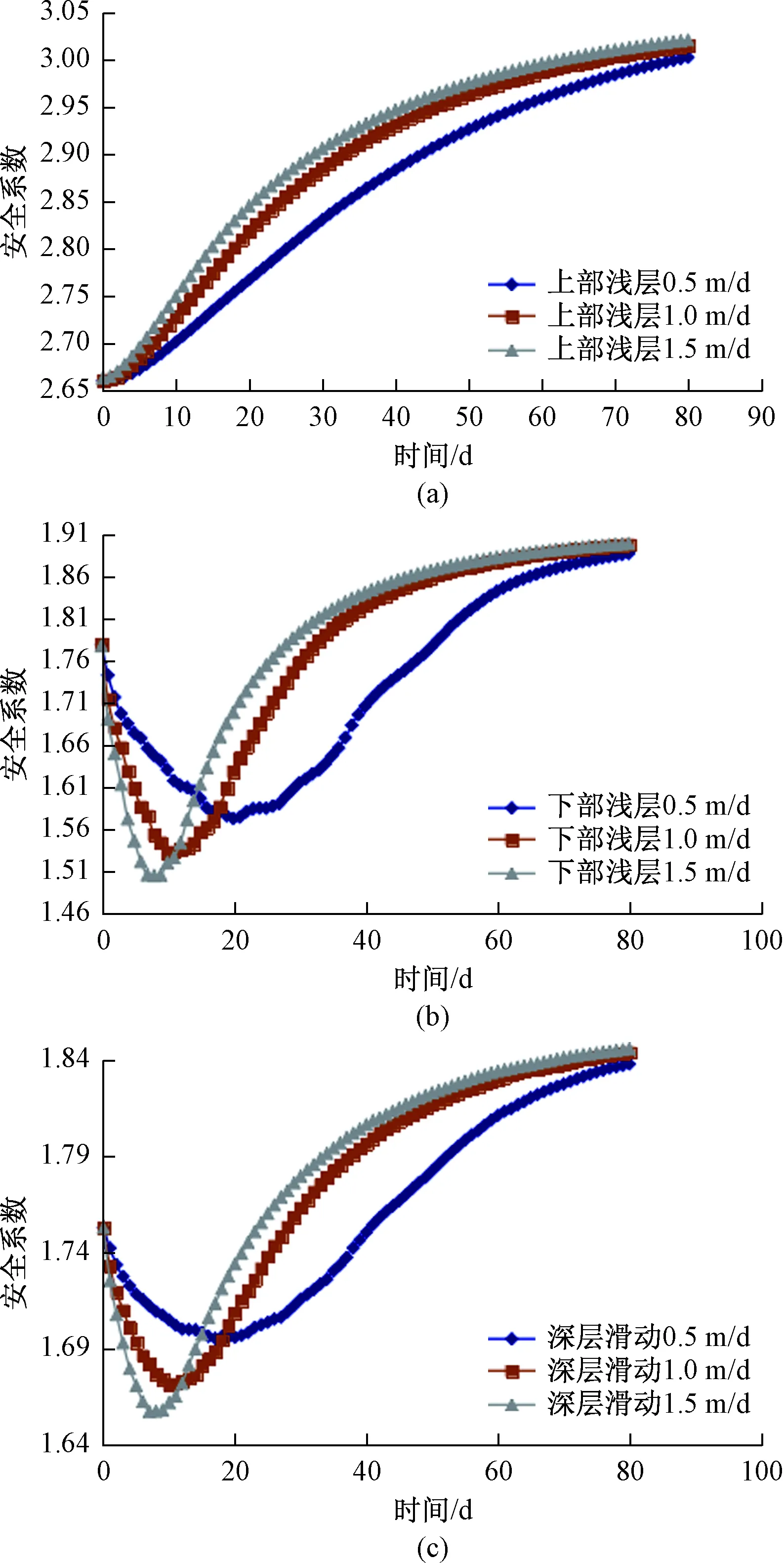
图6 工况1深层浅层滑坡稳定系数变化Fig.6 Variation of stability coefficient of deep and shallow landslide under calculation condition 1

由图6可见，不同位置滑坡在库水位骤降情况下的稳定系数变化有较大差异，对于上部浅层滑坡来说，库水位下降过程中上部浅层滑坡的稳定系数随着时间呈现不断增大的趋势，这是因为随着库水位下降，上部浅层的地下水位线逐渐下降，土体的强度及有效应力不断增大，从而上部浅层的稳定系数不断增大，同时发现库水位下降速率越大，上部浅层滑坡的稳定系数上升越快，但是最终稳定系数趋于一个稳定的值；对于下部浅层来说，稳定系数随时间呈现先下降后升高的趋势，这是因为库水位骤降过程中，库岸边坡存在一个水压卸载的过程，故稳定系数先下降，在库水位下降后滑坡内部的水位逐渐下降，从而土体的强度参数以及有效应力升高，从而稳定系数逐渐增大。库水位下降速率越大，最小稳定系数出现的时间越早，最小稳定系数也越小，最终不同库水位下降速率下稳定系数趋于一致。深层滑坡的稳定系数变化规律与下部浅层滑坡的稳定系数变化规律较为一致，但是稳定系数值有一定差异，下部浅层滑坡的最小稳定系数要小于深层滑坡的最小稳定系数，说明下部浅层在库水位骤降过程中先容易失去稳定，随后是深层滑坡的失稳，而上部浅层滑坡较为稳定。

4.2 静库水位+不同类型降雨工况

165 m静库水位联合不同类型降雨下不同监测点的孔压变化规律见图7。

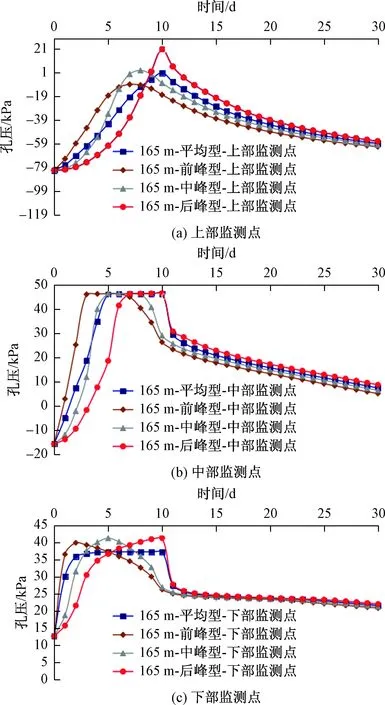
图7 工况2不同监测点孔压变化Fig.7 Variation of the pore pressure of different monitoring point under calculation condition 2

由图7可见，不同监测点在不同类型降雨条件下的孔压总体变化规律较为一致，即随着降雨的进行呈现先增大后降低的趋势，对于不同的监测点，孔压变化规律稍有差异，体现在最大孔压的出现时间以及最大孔压的值上。对于上部监测点，最大孔压达到最大的时间的先后顺序分别是前峰型、中峰型、后峰型、平均型，其中平均型所达到的最大孔压最大，中峰型与后峰型达到的最大孔压其次，前峰型最小；对于中部监测点，最大孔压达到最大的时间的先后顺序分别为前峰型、中峰型、后峰型、平均型，四种雨型所达到的最大孔压并无差异；对于下部监测点，最大孔压达到最大的时间的先后顺序分别是前峰型、中峰型、后峰型、平均型，前峰型、中峰型、后峰型降雨最大孔压较为一致，而平均型降雨最大孔压较小。

不同类型降雨条件下的滑坡深层浅层稳定系数变化曲线见图8。

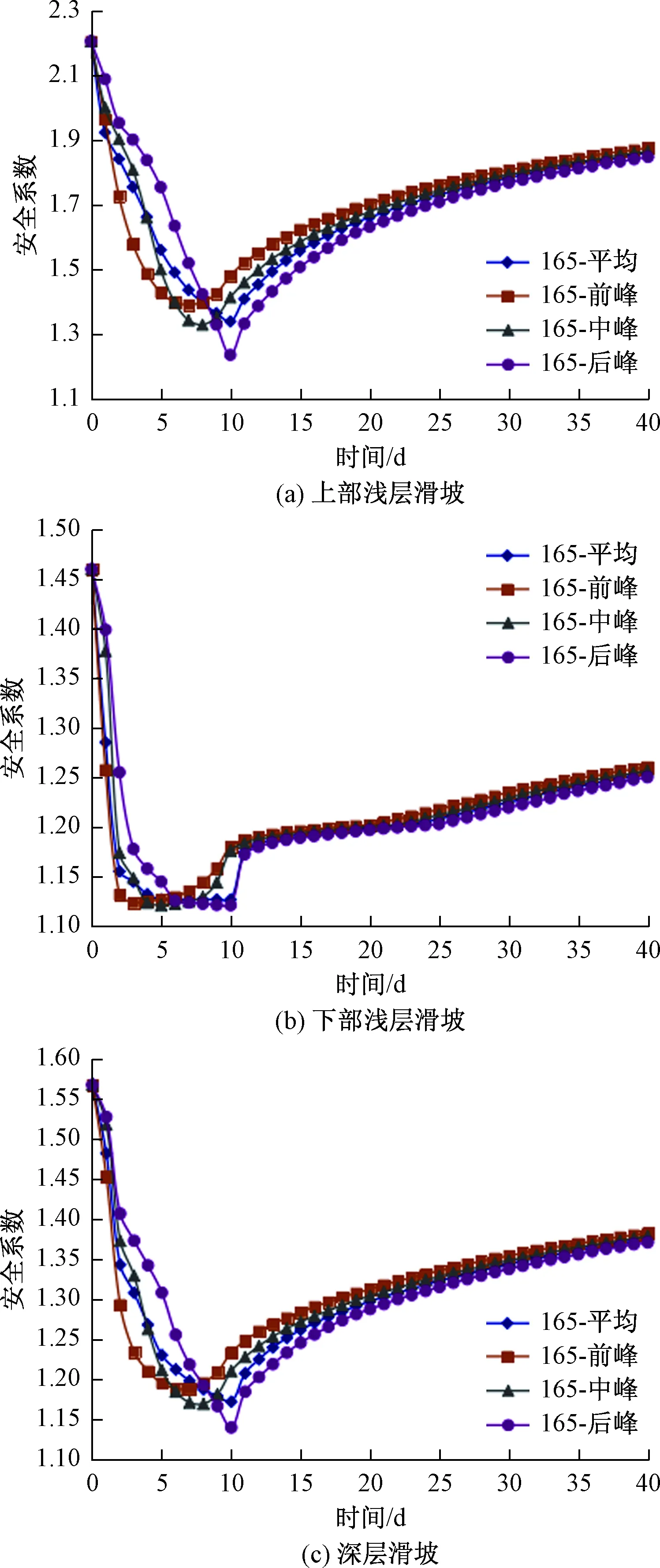
图8 工况2深层浅层滑坡稳定系数变化Fig. 8 Variation of stability coefficient of deep and shallow landslide under calculation condition 2

由图8可见，随着降雨的进行，不同类型滑坡的稳定系数随时间呈现先下降后上升最后趋于稳定的趋势，对于上部浅层滑坡来说，前峰型降雨最小稳定系数到达的时间最快，中峰型次之，后峰型再次之，平均型最慢，最小稳定系数数值前峰型最大，中峰型与平均型次之，后峰型最小；对于下部浅层滑坡来说，最小稳定系数到达的时间的快慢顺序依次为前峰型、中峰型、后峰型、平均型，最小稳定系数的数值几乎相等；对于深层滑坡来说，稳定系数变化规律与上部浅层滑坡较为类似。值得注意的一点是，同一工况的最小稳定系数大小分别是上部浅层滑坡>深层滑坡>下部浅层滑坡，表明不同类型降雨条件下滑坡失稳规律为先是下部浅层的局部垮塌，然后是滑坡的整体滑动。

4.3 库水位骤降+不同时刻降雨

由4.2节可知，不同类型降雨对滑坡监测点孔压的整体变化规律以及对滑坡的稳定性的变化规律影响较小，在本节工况中不考虑不同类型降雨的影响，仅仅以平均型降雨发生在库水位不同时刻进行讨论，不同监测点孔压变化规律见图9。

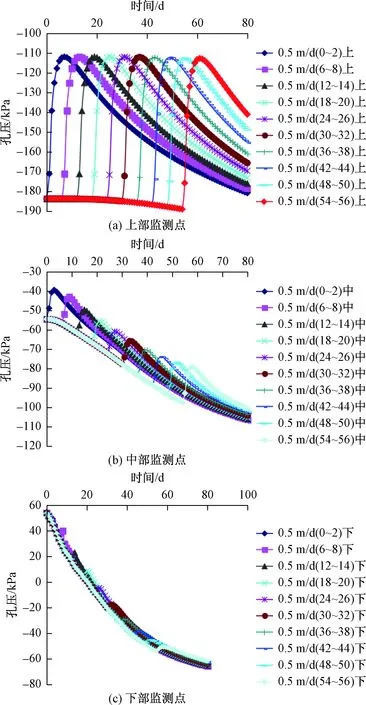
图9 工况3不同监测点孔压变化Fig.9 Variation of the pore pressure of different monitoring points under calculation condition 3

由图9可见，降雨发生在库水位不同时刻下不同监测点的孔压变化规律较为一致，即在库水位下降降雨发生时刻孔压有一个突然上升的过程，在降雨结束后孔压逐渐消散，对于上部监测点来说，降雨条件下孔压上升幅度较大，平均上升幅度为70 kPa，对于中部监测点来说，降雨条件下孔压上升幅度较小，平均孔压上升幅度为20 kPa，对于下部监测点来说，平均孔压上升幅度为5 kPa,可见随着监测点距离库岸的距离越近，降雨对滑坡体的影响逐渐削弱，而库水位对滑坡体的影响逐渐变大。

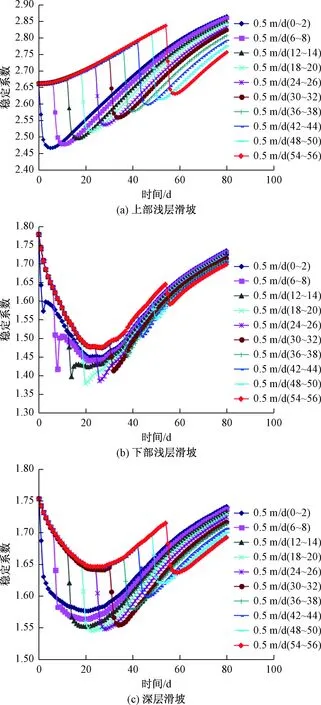
图10 工况3深层浅层滑坡稳定系数变化Fig. 10 Variation of stability coefficient of deep and shallow landslide under calculation condition 3

相应的稳定系数变化曲线见图10。由图10可见，稳定系数总体变化规律差异较大，对于上部浅层滑坡来说，稳定系数先增大，降雨发生时刻有一个明显的突降，停雨后缓慢上升，并且降雨发生的时刻越早，最小稳定系数出现的时间也越早，同时最小稳定系数越小；对于下部浅层滑坡来说，总体上稳定系数呈现先减小后增大的趋势，同时在降雨发生时刻有一个明显的下降，对于本次工况来说，当降雨发生在18～20 d时，最小稳定系数最小为1.37；对于深层滑坡来说，稳定系数变化规律与下部浅层滑坡较为一致，但是数值略有差异，最小稳定系数发生时刻也为降雨18～20 d，最小稳定系数为1.53，略大于下部浅层滑坡，可见下部浅层滑坡在降雨条件下失稳要先于深层滑坡。