海水位上升条件下软土地基竖向位移数值模拟分析

杨 逾,袁 杰,王树达

(辽宁工程技术大学土木工程学院，辽宁 阜新 123000)

0 引言

在过去的几十年里，潮汐所产生的效应一直受到相关领域的关注，关于潮汐产生能量的利用已取得了显著的成果，例如潮汐发电站的应用遍布各地。专家学者们对地基受潮汐作用的影响及软土地基加固处理技术这一问题的研究从未停步。潮汐对地基的影响主要表现在涨潮过程中海水水位不断上升导致地基中土体孔隙率提升，孔隙水压力增大，地基固结度增加，严重情况甚至威胁到地基的稳定。自1856年达西(Darcy)经大量的试验研究总结出渗透能量损失与渗流速度之间的关系定律以来，渗流力学在各个工程领域都取得了长足的发展，并在实际应用中取得显著成效[1～6]。刘杰等[7]依据国内外岩土渗流参数反问题研究现状，对参数辨识不适定性展开讨论，并提出初浅看法；刘占芳、刘全虎等[8]依据混合物理论的两相多孔介质理论，充分考虑固结过程中的水土耦合作用，通过建立数值模型，对饱和软土的弹塑性固结沉降过程进行分析研究；赵瑜、李晓红等[9]通过数值模拟，基于现代分形理论，分析了地下水在岩体内的运动规律；张冬梅、张印等[10]基于复变函数的映射变换，分析了不同渗流条件下孔隙水压力分布及地层和隧道长期沉降发展规律；董建军等[11]研究了随河水水位上升，河水径向渗流对河岸基坑及土体位移规律；杨天鸿等[12]总结了破碎岩体渗流突水的研究现状，得出破碎岩石渗流规律。但就在海水涨潮过程中，渗流作用对经加固后地基的影响鲜有研究。

采用数值模拟对经加固后的地基进行反演预测可能会存在土性参数选取不够精确，土层分布与实际情况存在差异等情况，但通过模拟，利用已有数据和相似模拟实验等相关资料，建立合理的数值模拟模型，通过不断修正与改进，对未来几年甚至十几年的情况进行预测，给实际施工方案提供依据和施工思路。本文以深圳市某填海区为例，针对软土地基选取一种加固措施，通过室内试验确定各土层土性参数，以FLAC3D软件为平台就地基在加固后受渗流作用的情况进行模拟，对地基竖向位移进行预测，分析了随海水水位上升，渗流作用对地基竖向位移的影响规律，对实际工程的地基沉降问题提供有益的借鉴和研究依据。

1 工程概况

1.1 工程背景

深圳市后海湾填海区总计划面积达4.2 km2，填海区原地质条件为海相沉积带，场地淤泥面标高为-0.50～1.50 m，并沿渗流方向缓慢降低，海水平均深度2.7 m，最高潮位为1.8 m，平均高潮位0.3 m，最低潮位-2.23 m，平均低潮位为-1.06 m，大多数的淤泥面出现在低潮位，现场实测土性参数见表1。

软土地基具有含水率高、渗透系数小、承载能力差等特点，沿岸土体表现更为明显，导致软土地基的加固难度大大提升。后海湾地区由于受潮汐对地下水位的影响，软土在含水量高时极易发生压缩变形，引起基础较大沉降，从而影响地基的稳定性。为提高地基承载力，施工中常常采用对地基进行加固的方法力求降低沉降对土体的影响。软土地基加固方法主要是强致密实、化学加固换置垫层、排水固结、四大类措施。传统夯实法施工，机器产生的噪音较大，引起的振动更有可能造成周围居民的不适；化学加固法成本高，施工要求严格，不适宜大面积施工；换置垫层法对于荷载不大的建筑物地基更为有效。根据后海湾地区地形、地质、地貌情况，由于占地范围广、区域划分多，需要大量填方材料，考虑到淤泥层和人工填土层，结合软土地基加固方式及工程、水文地质条件，应采用真空联合堆载预压法对软土地基进行加固[13-14]。真空联合堆载预压法是通过在软土地基中打设竖向排水通道(PVD)，并在软土地基土体通过真空泵施加负压，将软土地基内部水、气排出，加速软土地基的固结速率，达到提升地基承载力的目的。在荷载作用下，土体孔隙率减低，地基发生沉降，土体强度得以提高，地基承载力得到显著提升。真空联合堆载预压法加固机理为：排水固结作用、软土再固结作用、压密作用。其中，施工期180天，真空联合堆载预压期180天，卸载期30天，验收期30天。施工示意图如图1所示。

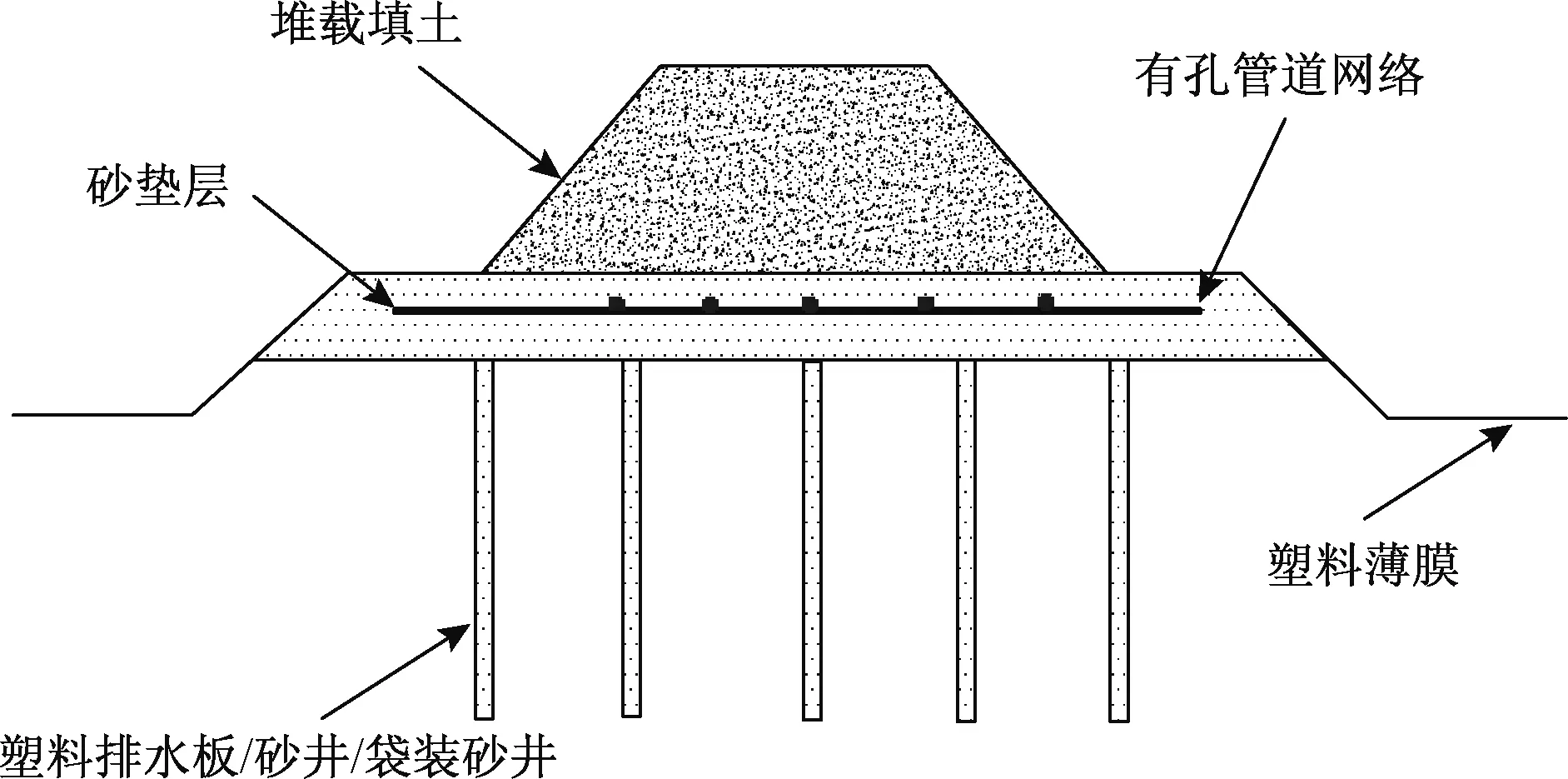
图1 真空联合堆载预压施工示意图Fig.1 Schematic diagram of combined vacuum and surcharge preloading

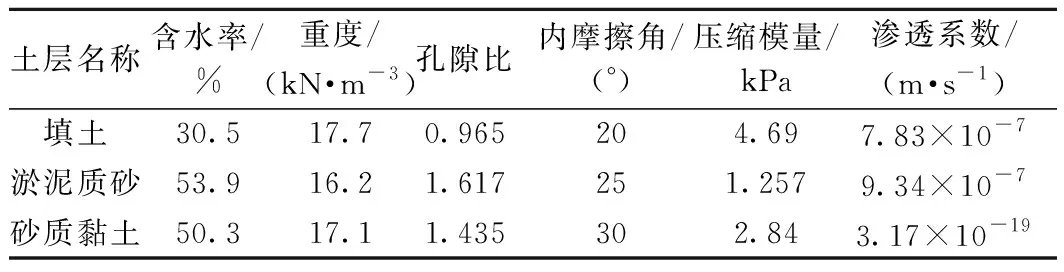
土层名称含水率/%重度/(kN·m-3)孔隙比内摩擦角/(°)压缩模量/kPa渗透系数/(m·s-1)填土30.517.70.965204.697.83×10-7淤泥质砂53.916.21.617251.2579.34×10-7砂质黏土50.317.11.435302.843.17×10-19

1.2 室内试验

以填海区某试验段位置采取的土样为原样，加工试件规格Φ×H(直径×高度)为50 mm×100 mm，试样分3组，每组制备场区不同土层试件5个，共计15个试件，为尽可能真实的还原填海区地质情况，将试样分别在不同的围压下固结稳定，施加不同的围压目的在于针对不同的深度。

试验得出地基经加固后各土层土性参数见表2。

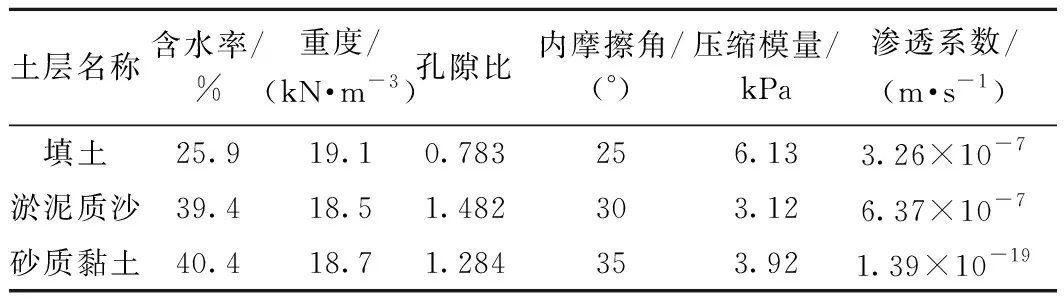
表2 加固后土性参数Table 2 Physical and mechanical parameters of the strengthened soil

2 渗流作用下数值模拟

2.1 模型建立假定

潮汐对地基的作用为非稳定渗流，即在渗透过程中，水头和流速均随时间发生变化。数值模型建立时，为简化计算，便于研究工程实际问题，作出如下五个假定：

(1)地基中各土层沿其长度方向是等厚度的；

(2)地基中各土层均为各向同性的均质体；

(3)各土层中的渗流均符合达西(Darcy)定律；

(4)考虑到地基中相邻土层之间的水量交换不大，可忽略不计；

(5)不考虑土和水的压缩性。

2.2 渗流理论

1856年，达西(Darcy)在装满砂的圆桶中进行试验，得出：

(1)

式中：V——断面平均流速(cm2)；

Q——流量(cm3·m-1)；

A——垂直于水流方向的过流断面面积；

K——渗透系数；

J——水力梯度(cm·m-1)。

1950年，雅各布(Jacob)提出土和水均为弹性体可压缩，并经推导得出：

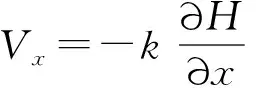
式中：α——土体压缩系数;

β——水压缩系数。

(3)

式中:μs——贮水系数。

2.3 模型建立

取填海区试验段某位置建立三维可视化模型，模型的长、宽、高分别设置为140 m、140 m、18 m。按场区条件整个模型分：第四系上更新统冲洪积层、第四系全新统海相沉积层、人工填土层共取3个层位。模型竖向施加自重应力，顶面为应力边界，底面施加约束，模型两侧面设置为自由边界。除施加自重产生的侧压以外，还施加了具有一定梯度的水平应力，将室内试验得出的土性参数进行折减[15]，调整为适用于模拟的力学参数，模型初始平衡采用Mohr-Coulomp模型进行计算，非稳定渗流模拟过程中，建立Drucker-Prager弹塑型模型，采用显示渗流算法，并通过编辑fish语言模拟潮汐的涨潮过程，以每天2∶00和14∶00为涨潮时间，编译流体时间(fluid flow time)、流体时间步(fluid flow timesteo)及不平衡流体变化率(current unbanlanced fluid flow ratio)控制时间参数，忽略土和水本身的压缩性，渗流模拟流程见图2。

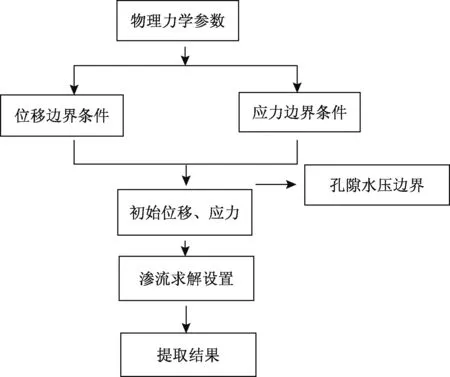
图2 渗流模拟流程图Fig.2 Flowchart of seepage simulation

2.4 数值模拟结果

设置孔压边界条件，模拟在初始水位和水位上升的0.3 m、0.6 m、0.9 m、1.2 m、1.5 m、1.8 m共七种情况下，渗流力对地基的影响。

(1)孔隙水压力

在涨潮时，随水位上升孔隙水压力的变化过程如图3所示。从图3中可以看出，在初始水位时，地基保持稳定状态；当水位上升0.3 m时，孔压值有聚增现象，在随后的水位上升过程中，孔隙水压力逐渐趋于平稳。最大孔隙水压力出现在地基临水面下部距地表5 m以下的范围内，水位突然上升时，地基内外水头差增大。孔隙水压力随地基深度的增加而增大。

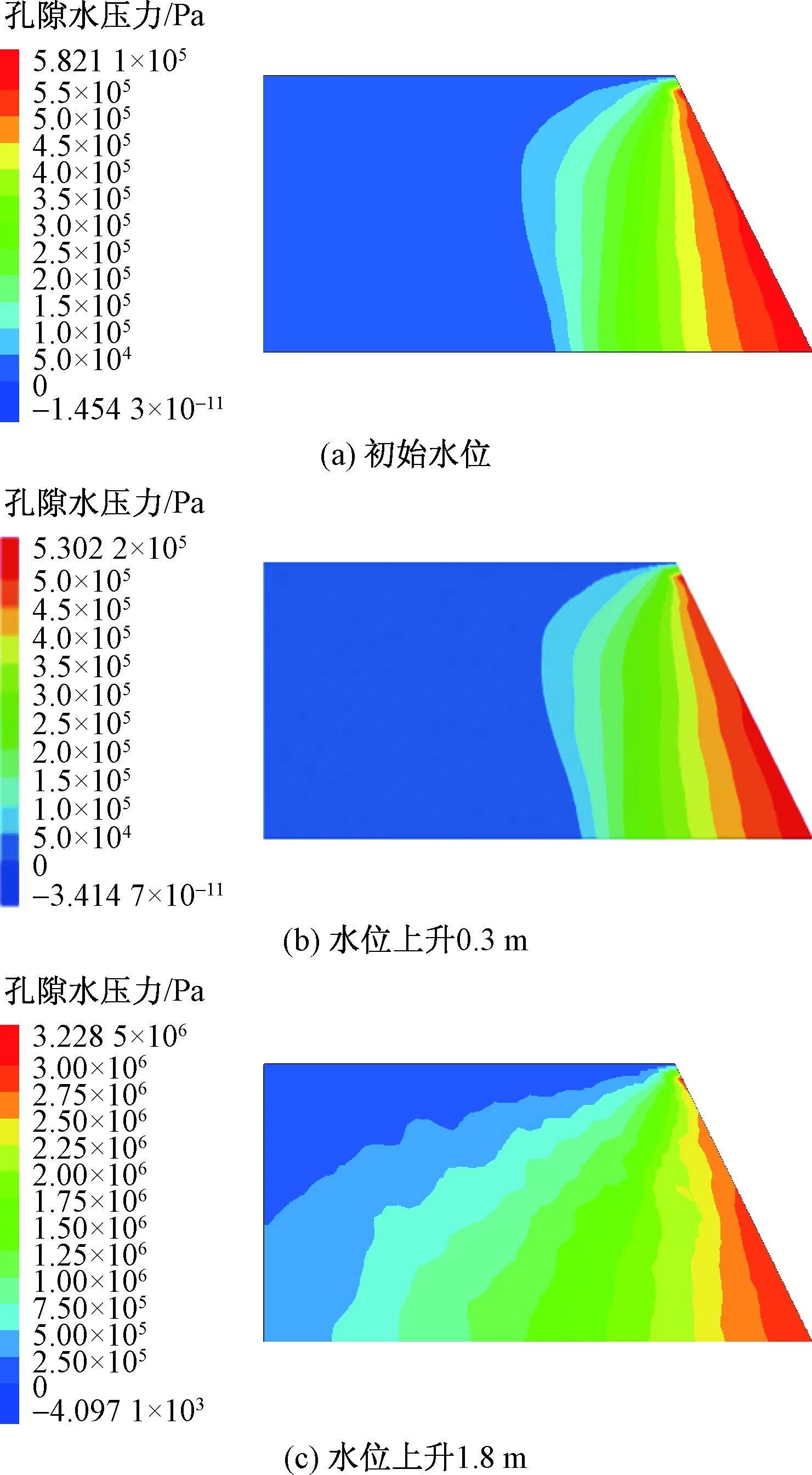
图3 土体孔隙水压力云图Fig.3 Contour of pore pressure of soil

(2)土体沉降

在涨潮时，随水位上升地基竖向位移变化如图4所示。从图4中可以看出，初始水位时，地基保持稳定状态，最大竖向位移出现在地基临水面坡顶处，并沿渗流方向呈阶梯式递减；水位上升过程中，竖向位移逐渐增大直至趋于平稳。

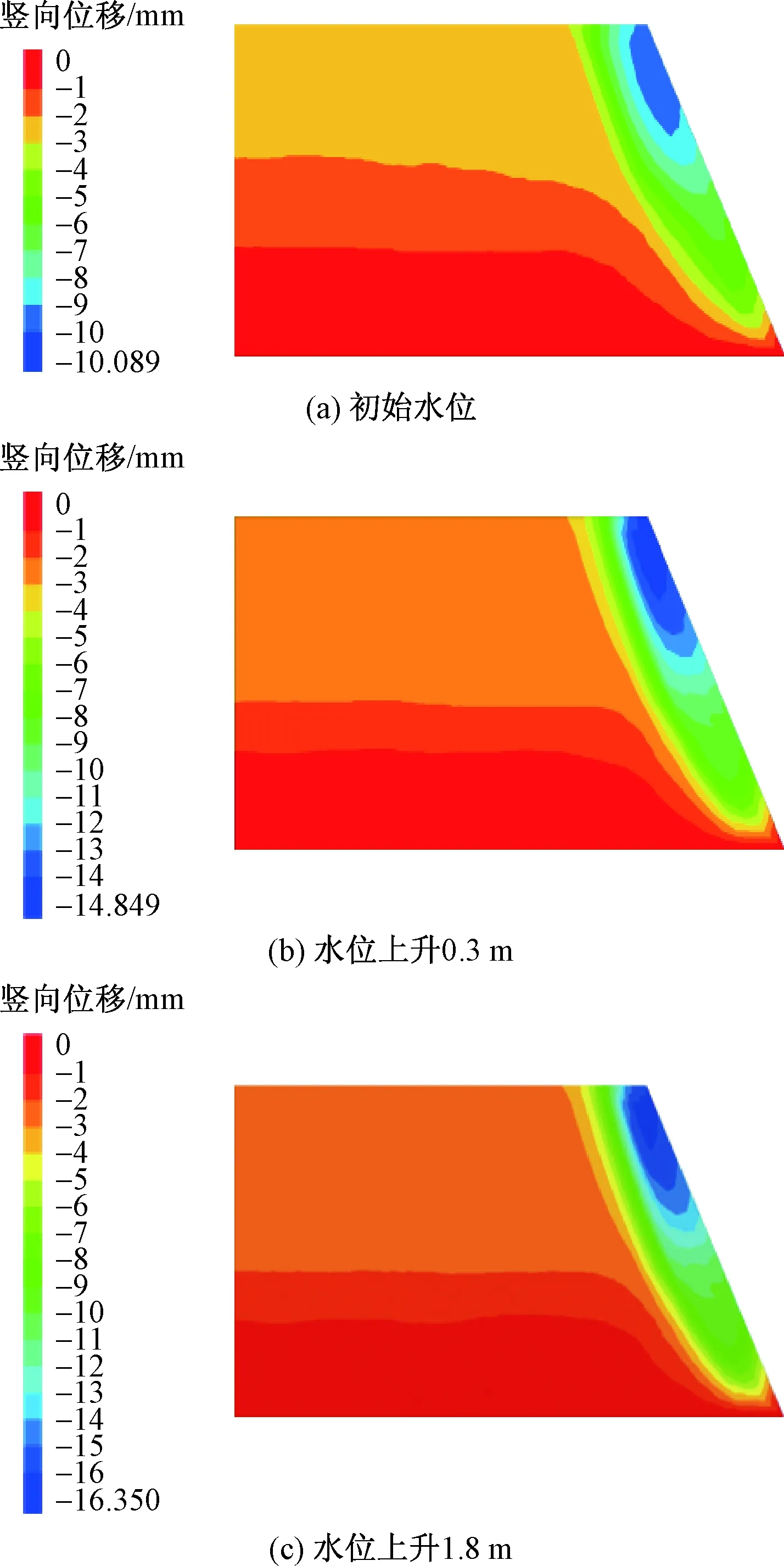
图4 土体竖向位移云图Fig.4 Contour of vertical displacement of soil

3 地基竖向位移分析

3.1 土体应力

土体应力的变化能够反映地基的稳定状态，土体应力随水位上升的变化规律如图5所示。图5(a)显示了土体最大剪应力随水位上升的变化规律。在水位上升0.3 m至0.9 m过程中，渗流作用对剪应力影响显著，剪应力增量与初始水位相比变化较大；在水位上升0.9 m至1.8 m的过程中，虽然剪应力继续增大，但增量逐渐减小直至趋于平稳。

图5(b)显示了地基最大水平应力随水位上升的变化规律。在地基斜坡坡顶，会出现明显的应力集中现象。相对于初始水位，水位上升0.3 m时，最大水平应力增加最为明显; 在水位上升0.3 m至1.8 m的过程中，最大水平应力基本呈线性增加。

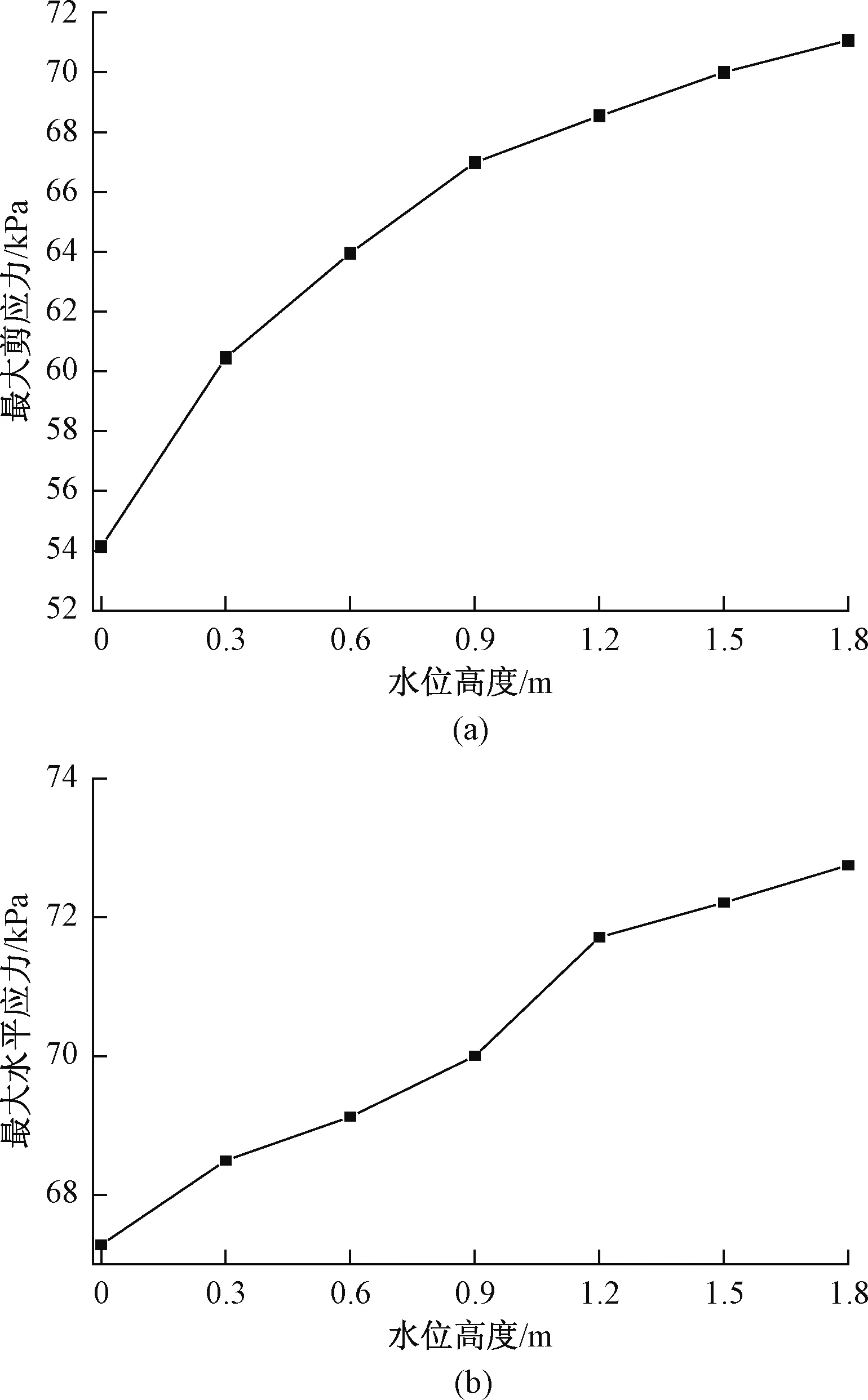
图5 土体应力曲线Fig.5 Stress curve of soil

3.2 土体沉降

地基沉降超过一定范围时，基础因受到影响会发生失稳，因此，应着重考虑沉降对土体的影响。地基沉降与水位高度密切相关，在涨潮过程中，水位不断升高，渗流力逐渐加大，地表沉降相对显著，初时曲线斜率大，而之后的曲线斜率逐渐减小至趋于平缓。

图6显示了涨潮时水位不断上升直至最高潮位1.8 m时土体最大竖向位移变化规律。初始水位时土体的沉降量趋于稳定；由初始水位上升至0.6 m过程中，竖向位移变化较大；在水位由0.6 m上升至1.8 m的过程中，竖向位移呈缓慢增加趋势。

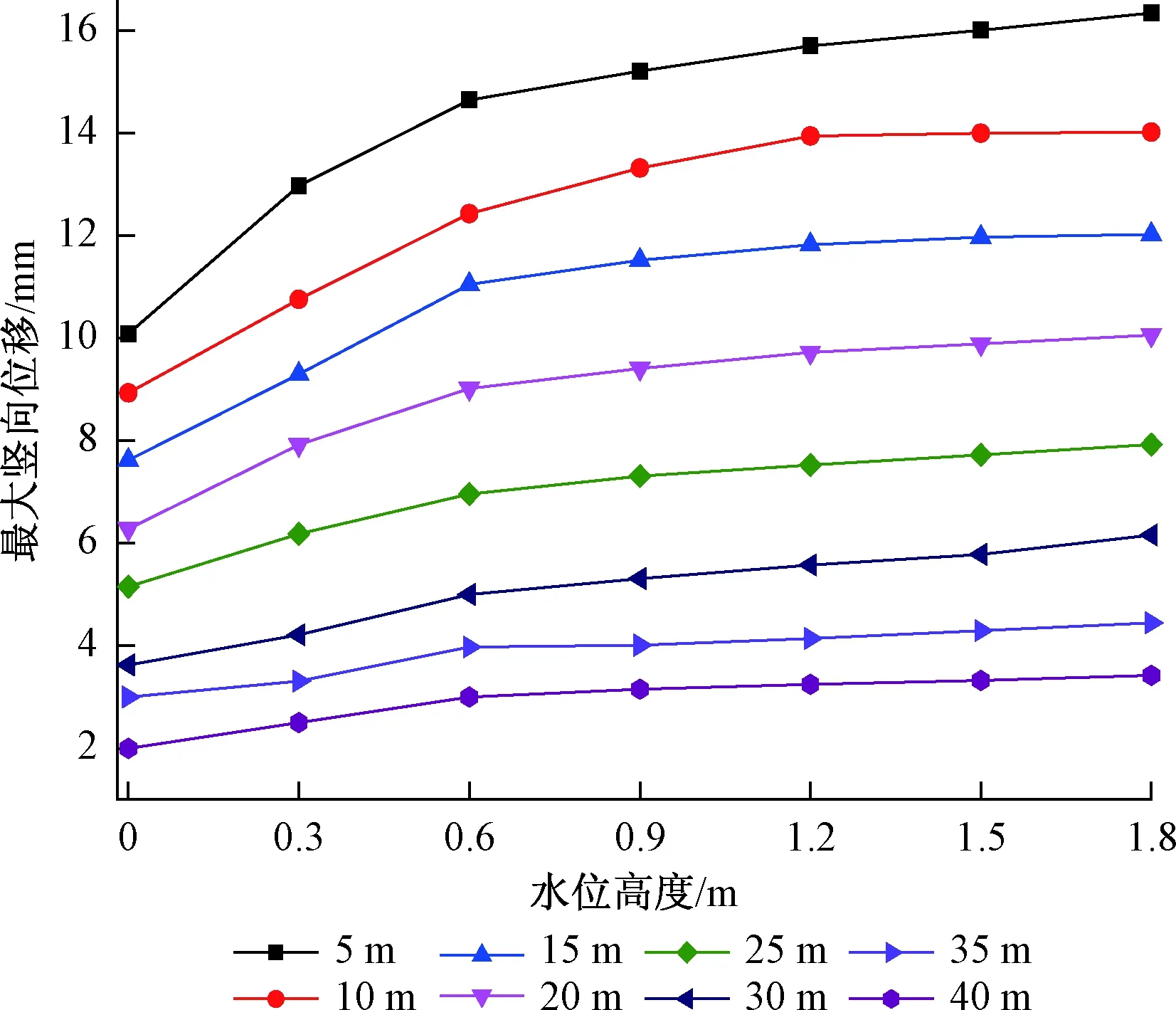
图6 土体最大竖向位移Fig.6 Maximum vertical displacement of soil

本文收集了填海区某试验段地基处理工程中随水位上升实测沉降量的变化曲线，并与模拟值对比，从图7中可以看出数值模拟的地基沉降速率与实测中的地基沉降速率较为接近且沉降量相差无几。

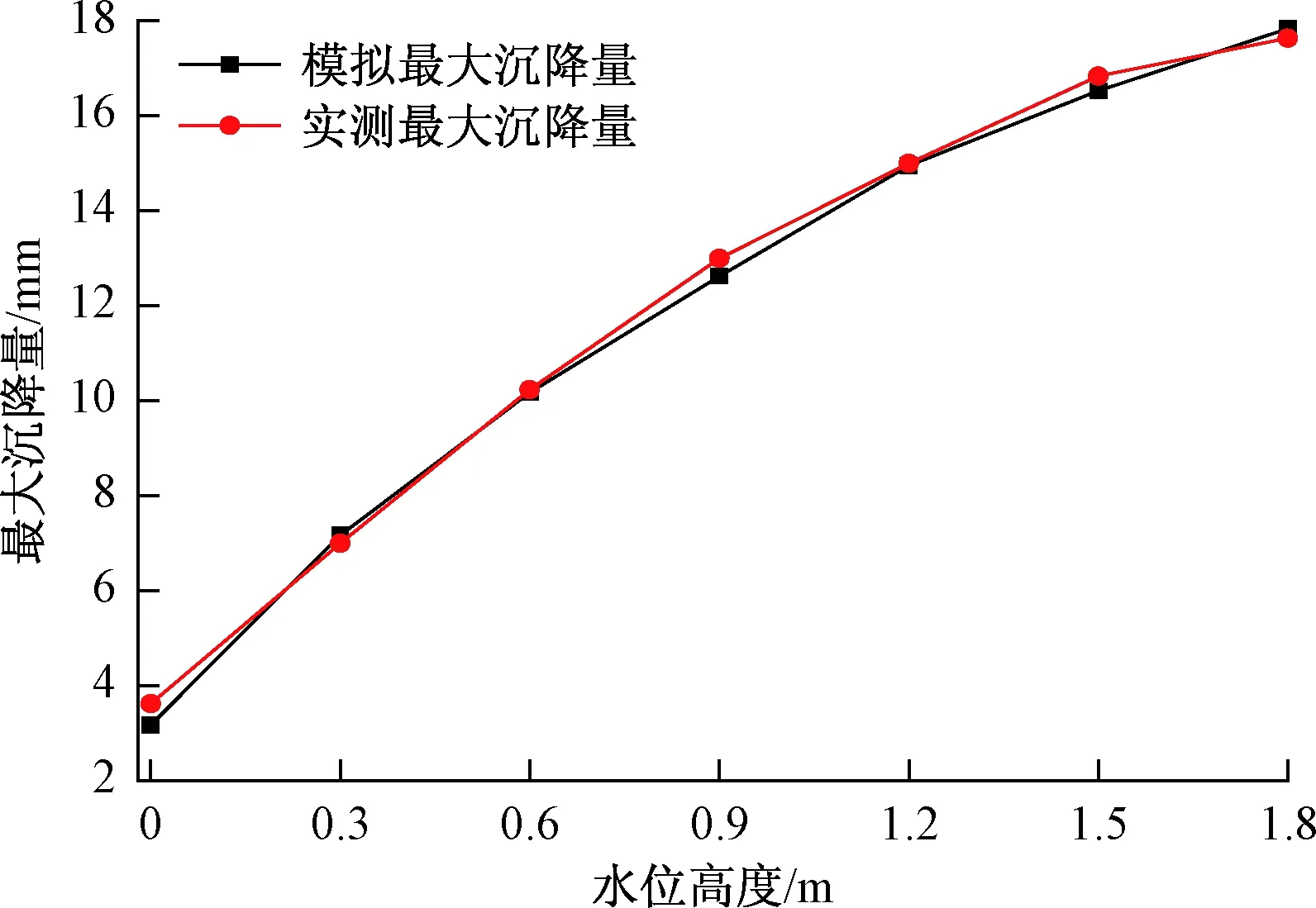
图7 数值模拟与实测的对比沉降Fig.7 Displacement of numerical simulation and the measured displacement

3.3 土体固结系数

地基经加固后，土体由超固结状态(OCR>1)转变为卸载回弹及之后的次固结沉降，通过确定固结系数对次固结沉降量进行估算[16]。在渗流作用下，土体空隙中的自由水由于流动，致使土体孔隙体积发生变化；随着固结压力增大，超静孔隙水压力增大，促进孔隙水的渗透；当土体固结到一定程度后，渗透系数趋于一定值，致使其固结系数不再发生变化。

(4)

式中:Cv——土的固结系数(cm2/s);

k——渗透系数;

γw——水的重度，一般近似值等于10.0 kN/m3;

e——天然孔隙比;

a——压缩系数。

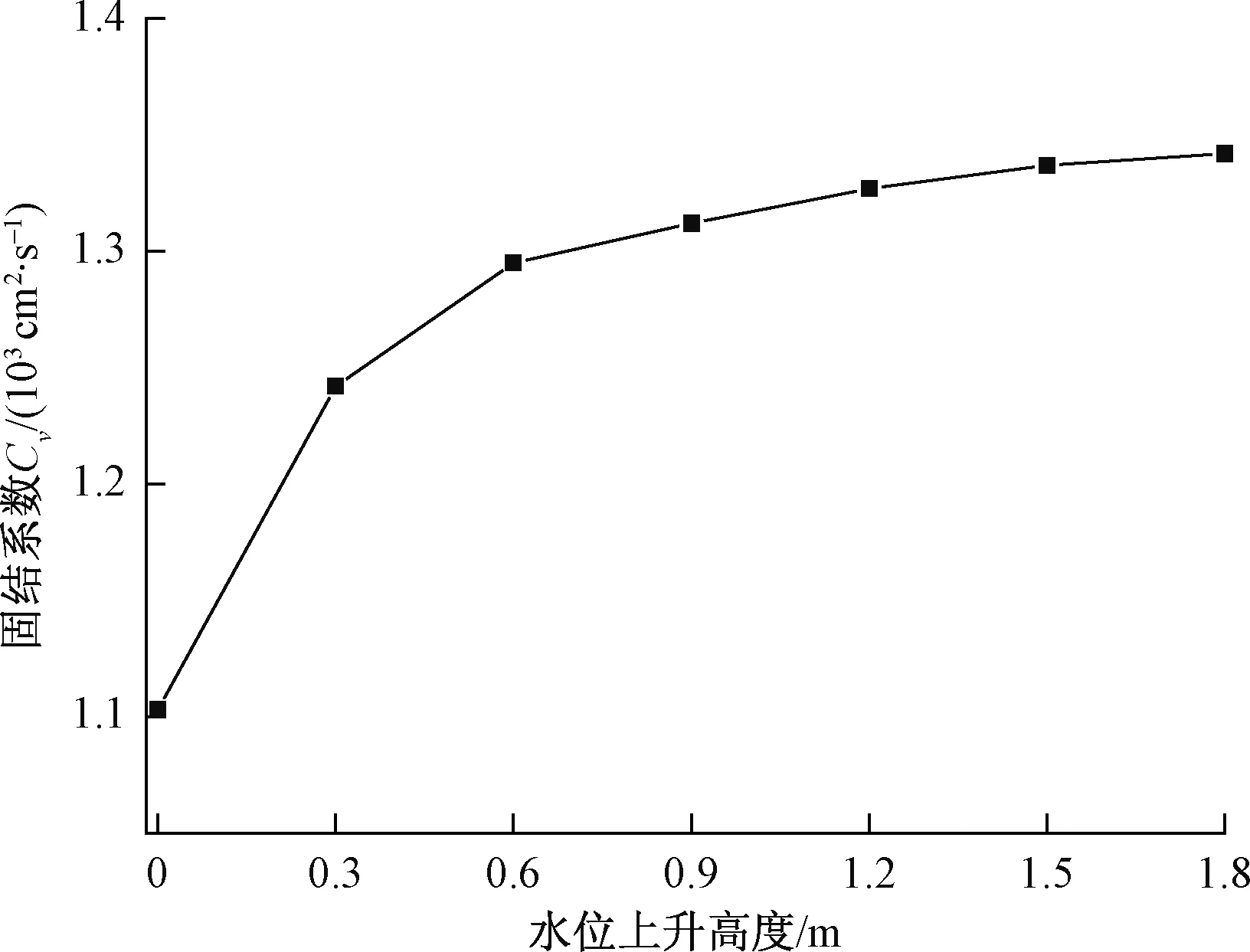
图8 固结系数Fig.8 Coefficient of consolidation

不同水位条件下的土体固结系数如图8所示。从图8中可以看出，在初始水位上升至0.3 m过程中，固结系数明显增加，渗流作用对地基影响最大；在水位上升0.3 m至1.8 m的过程中，固结系数趋于一定值。

结合实测资料，根据对地基竖向位移变形的规律及特点分析，总结出地基竖向位移变化基本上会经历三个过程：在初始水位时，地基处于平衡状态，竖向位移保持在一定水平，仅发生微小波动；随涨潮时间的增加，海水水位不断上升，孔隙水压力增大，土体的竖向位移随时间的推移而持续增加，沉降速率趋于平稳，土体固结系数逐渐增大至一定值；当水位最高值时，沉降达到极限状态，此时地基竖向位移为地基最大竖向位移。因此，可认为地基在沉降变化过程中会经历“平衡—发展—极限”三个阶段。

4 结论

(1)地基有多种加固方式，应因地制宜，根据具体情况具体分析。本文针对填海区地基的实际水文地质情况，对强致密实、化学加固换置垫层、排水固结、四大类措施进行比较，选择了真空联合堆载预压法对地基加固，并对该方法的作用机理和施工方法进行了研究。

(2)在水位上升过程中，通过数值模拟得出孔隙水压力沿渗流方向呈阶梯式递减，不同水位峰值均出现在地基临水面坡顶处，土体应力初期变化显著，后期趋于平稳。

(3)通过FLAC3D数值模拟，得出不同时间段地基沉降量，并与实际监测结果对比，得出模拟值与实际监测值基本一致，在规定允许变形范围内，可以认为数值模拟能够较为准确的预测地基的竖向位移。

(4)地基在沉降变化过程中会经历“平衡—发展—极限”三个阶段。且本次地基处理方案的选取及对其加固后受海水水位上升作用影响的分析处于科学、合理和可控状态。