基于轮间耦合力最小的四轮独立驱动电动汽车驱动力分配方法
2018-12-26马雷
易 星 张 云 马雷
(1.江西科技学院,江西 南昌 330098;2.燕山大学,河北 秦皇岛 066004)
1 引言
环境污染与能源紧张已成为当今焦点问题,开发无污染,低能耗汽车成为迫切之需。电动汽车是汽车研究领域的热点之一。四轮独立驱动电动汽车可实现底盘电子化和主动化,使其与传统汽车相比具有更强的竞争力[1]。对于四轮独立驱动电动汽车驱动力分配方法,国内外学者进行了相关研究:文献[2、3]通过仿真分析,主要根据各驱动轮的纵向和侧向附着建立二次型评价函数,利用优化理论使车辆各驱动轮纵向和侧向附着最小,来实现驱动力分配,但优化时,需精确估计各车轮的侧向力;文献[4、5]利用轮胎模型,将轮胎侧向力近似用纵向力表示,建立驱动力分配目标函数,并进行了仿真实验,但在计算轮胎侧向力时需得到车轮侧偏角和滑转率。综上所述,虽然相关驱动力分配方法在仿真条件下能取得较好效果,但有些物理量无法用传感器测量不利于工程实际应用。
以四轮独立驱动电动汽车为研究对象。首先,分析某一驱动轮的受力情况及轮间耦合关系,得到轮间耦合力F的解析式,并分析F对车辆行驶动力性和稳定性的影响。然后,将F转化为对应驱动转矩作为目标函数;综合考虑影响驱动力分配的条件来确定约束条件,并确定约束条件中横摆转矩MZ的求解;最后,设计整车控制方法并建立ADAMS与Matlab联合仿真模型,通过分析仿真和实车实验结果,证实了基于轮间耦合力最小的驱动力分配方法的有效性和合理性。
2 驱动力分配策略
2.1 轮间耦合关系分析
驱动轮通过悬架固定于车架,车辆行驶时某车轮驱动力通过车架传递给其它车轮,各驱动轮互相拖拽,产生耦合力。驱动轮的纵向受力分析,如图1所示。
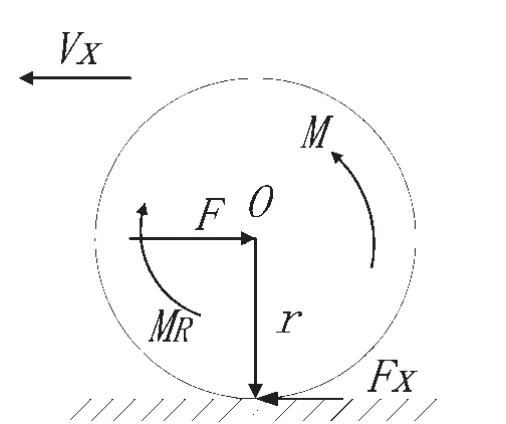
图1 驱动轮受力分
图1中,O为车轮滚动中心,r为车轮转动半径,Vx为汽车纵向速度,F为作用于车轮轴的纵向力,Fx为地面对车轮的切向作用力,M为车轮驱动转矩,MR为车轮滚动阻力矩。
车轮纵向力和力矩平衡方程为:

式中,J为驱动系统折算到车轮的转动惯量,ω为车轮转速,m为车轮及其簧载的总质量为车轮纵向加速度。
分析电机原理,电机转矩方程为:

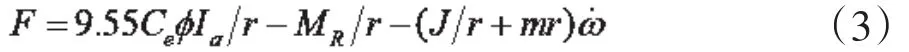
由此,定义F为其余车轮的作用力通过车架传递给目标驱动轮的力,F对目标驱动轮的影响即驱动轮轮间耦合问题。
2.2 耦合力F对车辆行驶的影响
当汽车行驶方向与某驱动轮的F值相同时,驱动轮的驱动力系数偏小,车轮滑移率偏小,附着裕度偏大;当汽车行驶方向与F值相反时,驱动轮的驱动力系数偏大,车轮滑转率偏大,附着裕度偏小[6]。当汽车在爬坡或急加速工况时,驱动力系数最大的驱动轮会最先出现滑转,从而导致四轮驱动不能达到最大驱动效果,由此增加功率损耗,甚至会影响汽车行驶的稳定性。
由于汽车在坡道、加/减速、转向情况会发生载荷转移,当F趋近于0或等于0时,4个驱动轮驱动力系数基本相同,均处于最好的附着条件,由此最大限度地利用垂直载荷较大的轮胎附着圆,增大了汽车的行驶稳态裕度。汽车行驶时,由于内外侧车轮产生纵向力之差,从而形成横摆力矩,可以提高车辆转向时的操纵稳定性。
3 驱动轮理想转矩求解
3.1 目标函数与约束条件建立
分析驱动轮轮间耦合关系可得,当四个车轮的F都为0或接近于0时,转矩分配比较合理。设计基于轮间耦合力最小的驱动力分配目标函数如下:

将耦合力转化为关于轮毂电机驱动转矩的目标函数为:
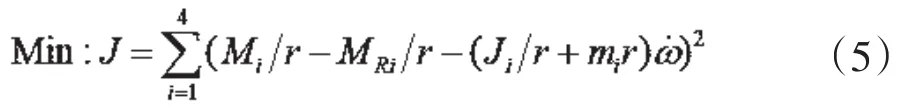
约束条件为:

式(4)-(6)中,i为车轮代号。Mi为车轮驱动转矩,MZ为通过车辆二自由度模型得到的理想横摆转矩。
式(6)中,第一项为总驱动转矩的约束,即总驱动转矩等于总阻力转矩。第二项为对左右侧车轮驱动转矩的约束:直线行驶时,使左右侧车轮的驱动转矩相等,即横摆力矩为0;转弯行驶时,使左右侧车轮的驱动转矩之差在合理范围,即产生的直接横摆力矩不大于车辆转向所需的横摆力矩。第三项为对车轮驱动转矩的约束,使驱动转矩不大于电机最大输出扭矩。
3.2 横摆转矩MZ确定
约束条件中须确定横摆转矩MZ,MZ满足车辆二自由度转向动力学模型,如下:

式(7)中,β 为质心侧偏角,γ为横摆角速度,δf为前轮输入转角,vx为纵向速度。
在匀速行驶时,前轮转角阶跃输入下进入的稳态响应即等速圆周行驶,此时,,带入式(7)可计算得到名义横摆角速度γd,根据文献[8],将理想质心侧偏角βd设为0得:

则车辆转向时的横摆转矩为:
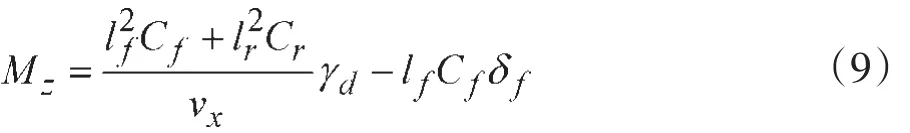
目标函数的求解选择约束条件下多变量寻优,仿真时用Matlab优化工具箱中fmincon函数求解,实验样车中应用罚函数法求解。
4 整车控制方法
在整车驱动控制过程中,实际转矩通过轮毂电机获取,各驱动轮理想转矩由驱动力分配方法求得,以最优控制理论为基础,将实际转矩与理想转矩之间的偏差作为控制输入量,实现对各驱动轮转矩的控制。驱动转矩控制实际是对轮毂电机电流的控制,根据四轮驱动力分配方法可以得到在当前状态下各轮毂电机的理想电流值,再通过反馈调节使各电机的电流值趋近理想状态[9]。整车控制结构如图2所示:
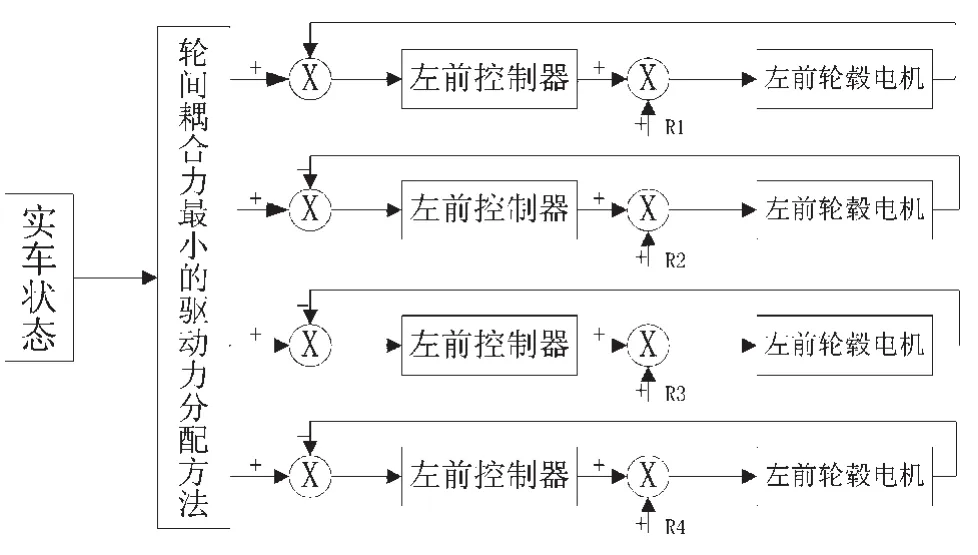
图2 整车控制结构
5 实车基本参数与ADAMS仿真建模
5.1 实车基本参数
实验样车为自行研制的四轮独立驱动电动汽车,由电源系统、动力系统、转向系统、制动系统和测控系统组成,通过VC++程序实现信号处理和整车控制[10]。样车基本参数如表1所示。
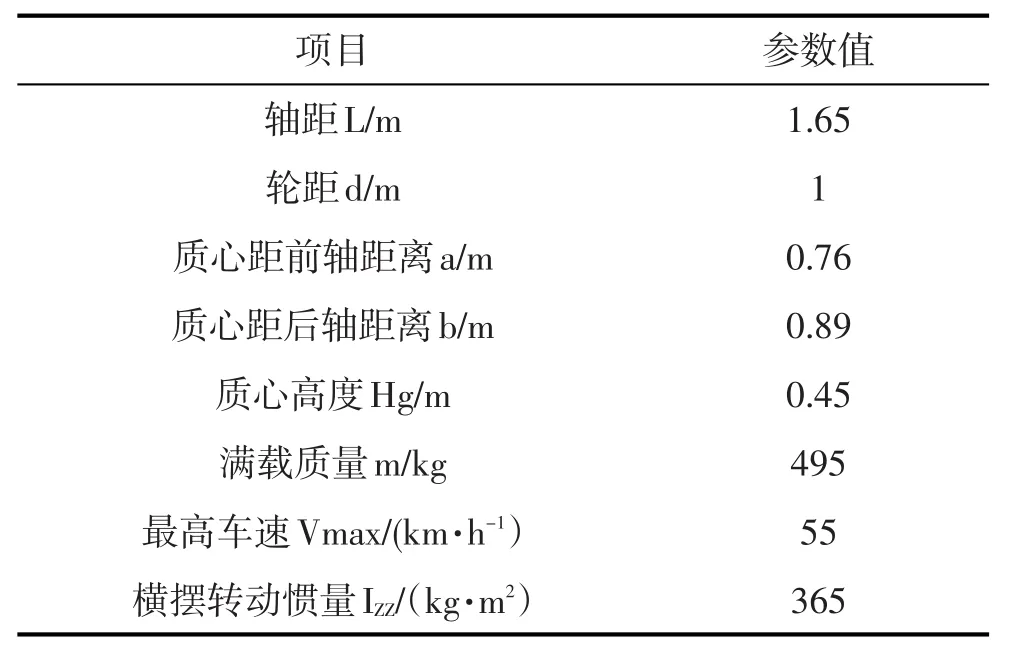
表1 样车基本参数
5.2 ADAMS仿真建模
为减少建模工作量,重点考虑车辆动力学性能,须先对整车的相关系统和部件进行简化。然后在ADAMS/View模块中,以实验样车各参数为基础,结合实际行驶工况,选择UA轮胎模型和2d_flat地面谱,建立样车几何模型。如图3所示。

图3 4WID电动汽车ADAMS几
6 联合仿真分析
与其他驱动力分配策略相比,基于轮间耦合力最小的分配方法使得相关参量更容易通过传感器获得,同时也能得到较好的仿真和实验结果。本文以基于轮胎利用率最小的驱动力分配方法为例,与本研究方法进行仿真和实验对比分析。轮胎利用率最小的驱动力分配模型[2]如下:

式中,FX、FY分别为车辆纵向和侧向力,C为常系数。
考虑到各不同行驶工况对车辆性能的影响,选择匀加速变匀速直线和匀速直线变弯道两种复合工况进行联合仿真分析。
6.1 匀加速变匀速直线工况
在匀加速变匀速直线工况仿真中,设定车辆加速度为1m/s2的仿真时间为10s,之后保持匀速状态。图4为不同驱动方式下耦合力F的仿真结果。车辆直线行驶时,左右侧车轮受力情况相同,图4中只给出左侧车轮的仿真结果,其中,实线为左前轮,虚线为左后轮。

图4 不同驱动方式下耦合力F的仿真结果
分析图4(a),轮胎利用率最小驱动时,加速阶段耦合力F波动小,匀速阶段F接近于0。从图4(b)可看出,在轮间耦合力最小驱动下,加速阶段F只在开始瞬时有小变化,之后包括匀速阶F均接近于0。即在这两种驱动方法控制下,F的变化相似。
图5为匀加速变匀速直线工况下,上述两种驱动方式的滑移率仿真结果:

图5 不同驱动方式下滑移率的仿真结果
如图5所示,在加速阶段,滑移率稳定在0.06,在匀速阶段,滑移率平滑过渡,减小到稳定值0.01附近。在该复合工况下,两种驱动方式的车轮滑移率变化非常相似,即耦合力最小驱动方法也能得到与其他方法类似的滑移率变化。
6.2 匀速直线变弯道工况
在匀速直线变弯道工况仿真中,设定车速为20 m/s,对前轮向左施加2°的转角,图6分别为轮胎利用率最小和轮间耦合力最小驱动方式下耦合力F的仿真结果。

图6 不同驱动方式下耦合力F的仿真结果
如图6所示,在该复合工况下,轮胎利用率最小和轮间耦合力最小两种驱动方式下,耦合力F在匀速阶段都出现一定的波动后稳定于0附近。表明在该复合工况下,这两种驱动方式的F也具有相似的变化趋势。
图7为匀速直线变弯道工况下,上述两种驱动方式的滑移率仿真结果:

图7 不同驱动方式下滑移率的仿真结果
如图7所示,在匀速直线变转弯工况下,轮间耦合力最小驱动与轮胎利用率最小驱动时,车轮的滑移率都相差很小,且变化趋势都是由开始的小波动趋于一个稳定状态。表明在这种复合工况下,耦合力最小驱动方法依然能够得到与其他方法类似的仿真结果。
综上所述,在匀加速变匀速直线与匀速直线变弯道两种行驶工况下,进行轮胎利用率最小和轮间耦合力最小两种驱动力分配方式的仿真实验,仿真结果表明:两种模式下的耦合力和车轮滑移率的变化相似,即轮间耦合力最小驱动策略均可以得到较理想的驱动效果。
7 实车实验
7.1 直线行驶实验
直线行驶实验中,实车加速阻力、道路阻力直接影响电机负载,再加上实验场地路面具有一定的不平度,导致车轮转速和电机电流的变化趋势存在相应差异。实验结果如图8所示,(a)、(b)、(c)分别为车轮转速、电机电流及目标与实际电流比对的变化曲线。
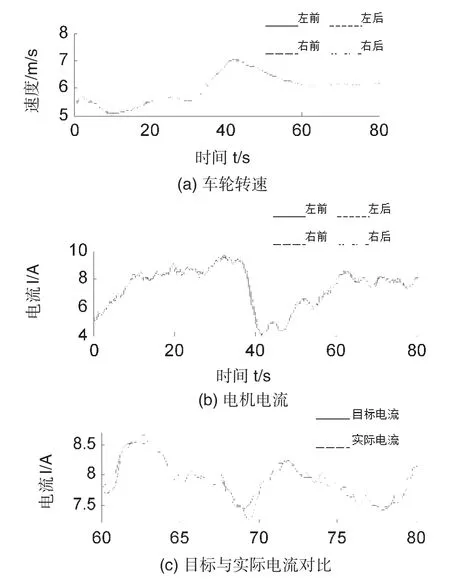
图8 直线行驶实验曲线
从图8(a)、8(b)可知,由于车辆加速度不大,载荷转移不明显,4个轮毂电机电流基本相同。图8(c)表明,实际电流变化趋势与目标值相互吻合,即电机电流在控制器的作用下可较好地跟踪优化电流值,验证了电机控制器的合理性。
7.2 转弯行驶仿真与实验
受实验条件限制,圆周行驶实验只在较低车速下进行。设定车速为4.3 m/s、前轮转角为0.17 rad,为便于分析,将车轮转速转化为车轮质心速度。分别对轮速和电流进行了联合仿真和实车实验,结果如图9、10所示。
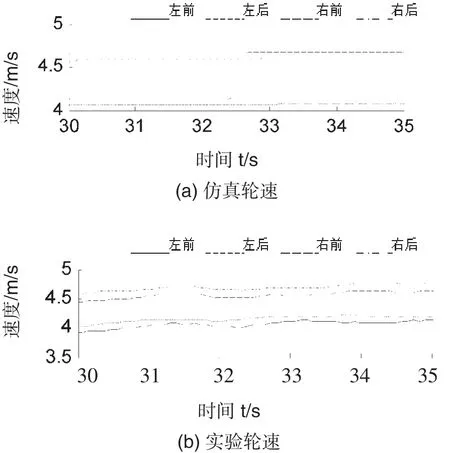
图9 仿真和实验的轮速变化曲线

图10 仿真和实验的电机电流变化曲线
分析图9、10,在转弯行驶条件下,仿真与实车实验的四轮转速、电机电流都基本吻合。实车实验的轮速、电流波动是由实验场地不平引起的,属于正常现象。
综上所述,在直线行驶工况下,实车实验结果验证了所设计整车控制器的合理性;在转弯行驶工况下,仿真与实车实验结果基本吻合,变化趋势一致。表明基于轮间耦合力最小的驱动力分配方法可以合理的分配4个车轮的驱动转矩。
8 结束语
(1)通过分析驱动轮轮间耦合关系,建立驱动转矩目标函数和约束条件,经优化求解,得出基于轮间耦合力最小的各轮理想驱动转矩。
(2)建立Adams与Matlab联合仿真模型,以最优控制理论为基础,设计整车控制器,实现对各驱动轮转矩的控制,得到整车控制策略。
(3)对比分析联合仿真与实车实验结果,在直线和转弯工况下,实验与仿真结果吻合,轮间耦合力最小的驱动力分配策略可根据车辆载荷转移情况合理分配各车轮的驱动转矩,效果显著。
