Analysis and Improvement of an Efficient Controlled Quantum Secure Direct Communication and Authentication Protocol

Jifeng Zhong ,Zhihao Liu and Juan Xu

1 Navigation College,Jimei University,Xiamen,361021,China.

2 School of Computer Science and Engineering,Southeast University,Nanjing,211189,China.

3 Κey Laboratory of Computer Network and Information Integration,Southeast University,Ministry of Education,Nanjing,211189,China.

4 Institute for Quantum Computing,University of Waterloo,Waterloo,ON,Canada,N2L3G1.

Abstract:The controlled quantum secure direct communication(CQSDC)with authentication protocol based on four particle cluster states via quantum one-time pad and local unitary operations is cryptanalyzed.It is found that there are some serious security issues in this protocol.An eavesdropper(Eve)can eavesdrop on some information of the identity strings of the receiver and the controller without being detected by the selective-CNOT-operation(SCNO)attack.By the same attack,Eve can also steal some information of the secret message that the sender transmits.In addition,the receiver can take the same kind of attack to eavesdrop on some information of the secret message out of the control of the controller.This means that the requirements of CQSDC are not satisfied.At last,we improve the original CQSDC protocol to a secure one.

Keywords:Quantum cryptography,controlled quantum secure direct communication,selective-CNOT-operation attack.

1 Introduction

Now we have entered into the era of cloud computing and big data.The security of data becomes more and more important.The most efficient way is to encrypt the data with a private key.Although the one-time pad cryptosystem is with,but how to distribute a key with the proven security is really hard in classical cryptography.On the contrary,the proven secure key distribution problem can be effectively solved by the quantum manner [Bennett and Brassard(1984); Gisin,Ribordy,Tittel et al.(2002); Lo,Curty and Tamaki(2014)].In fact,there is a new secure communication way called as the quantum secure direct communication(QSDC)[Deng,Long and Liu(2003); Deng and Long(2004); Wang,Deng,Liu et al.(2005); Long,Deng,Wang et al.(2007); Liu,Chen,Liu et al.(2012); Liu,Chen,Liu et al.(2013); Li(2015)] where the secret message is communicated directly without being encrypted by a private key in advance.With the development of QSDC,many researchers put forward a new kind of QSDC,which is usually called the controlled QSDC(CQSDC)[Wang,Zhang and Tang(2006); Hassanpour and Houshmand(2014); Tan and Zhang(2016)].In CQSDC,at least one additional user,the controller,is introduced besides the sender and the receiver to control the communication.If the controller does not permit the sender and the receiver to exchange the secret message,the receiver cannot gain any useful information of the secret message.If and only if the controller permits the sender and the receiver to exchange the secret message,the receiver can obtain the sender’s secret message.We can summarize the basic requirements of CQSDC.Firstly,the CQSDC protocol should be secure against the external eavesdropper.Secondly,the receiver cannot gain any useful information about the secret message before the controller’s permission.

As the contrary side of cryptography,cryptanalysis is also an important and interesting branch of cryptology,which usually be viewed as the art of code breaking in quantum cryptology.In 2005,Lo et al.[Lo and Κo(2005)] said that“breaking cryptographic systems is as important as building them”.It assesses whether a cryptographic protocol is secure or not.For example,it assesses whether a cryptographic protocol has some potential loopholes,if so,it tries to mend these loopholes.Thus,cryptanalysis makes people to put forward more and more secure cryptographic protocols.Up to now,people have proposed many kinds of attack strategies,such as the denial-of-service(DoS)attack [Cai(2003)],the(partially)intercept-measure-resend attack [Liu,Chen,Wang et al.(2014); Liu,Chen and Liu(2016)],the correlation-extractability(CE)attack and its general case [Gao,Wen and Zhu(2007); Song and Zhang(2007); Gao,Qin,Wen et al.(2010); Qin,Gao and Guo(2010); Liu,Chen,Liu et al.(2011)],the teleportation attack [Gao,Wen and Zhu(2008)],the entanglement attack [Liu,Chen,Wang et al.(2014)],the different initial state attack[Yen,Horng,Goan et al.(2009); Liu and Chen(2018)] and so on.

Recently,a novel CQSDC with authentication protocol [Nanvakenari and Houshmand(2017)] was proposed by using four particle cluster states via quantum one-time pad and local unitary operations.In every transmission,the fourth qubit of each cluster state was used as controller’s permission,and the same qubit and the first qubit of the same cluster state are utilized to deduce two classical bits of information.Since only single particle measurement was needed,it was easier to implement and less expensive.The authors also claimed that the protocol was secure and feasible against both of the inside and the outside attacks.They thought the receiver’s and the controller’s identity strings were reusable with unconditional security since they did not announce positions and bases of decoy particles.However,it can be found that there are some security problems if this protocol is deeply taken into account.Some information of the receiver’s and the controller’s identity strings can be stolen without being detected by the selective-CNOT-operation(SCNO)attack from an eavesdropper(Eve).Furthermore,she can eavesdrop on some information of the sender’s secret message with the same attack.In addition,the receiver can take the same kind of attack to eavesdrop on some information of the secret message out of the control of the controller.This means that the requirements of CQSDC are not satisfied.Finally,the original CQSDC protocol is improved to a secure one.

2 The original CQSDC protocol

There are three users:Alice,Bob and Charlie who are the sender,the receiver,and the controller respectively.Bob has the secret N -bit identity string I DB,and Charlie has the secret N -bit identity string IDC.Alice shares IDBand IDCwith Bob and Charlie respectively,but Bob and Charlie do not share their identity strings.The original CQSDC protocol [Nanvakenari and Houshmand(2017)] is described as follows.

Step(1):Alice prepares an ordered sequence with Nnumber of four particle cluster states,each of which is staying in

where bn,tn,kn,cnare four correlated particles in the n-th cluster state.Then,Alice constructs the ordered Band C sequences by particles bnand cnrespectively.The remaining particles tnand knconstruct the ordered A sequence [t1,k1,t2,k2,,tN,kN].For convenience,we also denote the two subsequences [t1,t2,,tN]and [ k1,k2,,kN]by the Atsequence and the Aksequence respectively.

Step(2):If a bit of IDBis 0,Alice performs the unitary operation U0on the corresponding particle in the Csequence,otherwise the unitary operation U1is performed,whereU0=I= 0 〈0|+1〈1|and U1=iσy=0〈1|-1〈0|.Thus,we get a new ordered sequence,CU.

Step(3):Alice measures the A sequence in Zbasis and gets an ordered classical bit sequence TAwhich denotes [ TAT1,TAK1,TAT2,TAK2,,TATN,TAKN].Similarly,TAcan be divided into two subsequences TATand TAKwhich denote [ TAT1,TAT2,,TATN]and[TAK1,TAK2,,TAKN]respectively.For convenience,we let TAbe expressed as TATTAK.

Step(4):If a bit of TAKis 0,Alice performs U0on the corresponding particle in the B sequence; otherwise U1is performed.Thus,we get a new ordered sequence,BU.

Step(5):Alice prepares two decoyN-qubit sequences SIDBand SIDCaccording to I DBand I DC,respectively.The rule to prepare a qubit is that: the i -th qubit of SIDB(SIDC)is prepared in Zbasis if the i -th bit of I DB(IDC)is 0; otherwise,it is prepared in Xbasis.

Step(6):Alice mixes SIDBand SIDCinto BUand CUto form BU′and CU′respectively according to the following rule.The rule is:Alice puts the i-th qubit of SIDB(SIDC)just behind the i-th particle in BU(CU)if the i -th bit of I DB(IDC)is 0; otherwise,she puts the i-th particle in BU(CU)just behind the i -th qubit of I DB(IDC).After that,Alice transmits BU′and CU′to Bob and Charlie respectively.

Step(7):After Bob and Charlie receive BU′and CU′,they extract SIDBand SIDCaccording to I DBand I DCrespectively.Then Bob and Charlie measure each particle in SIDBand SIDCwith the right bases respectively.According to the measurement results,Bob and Charlie construct classical number sequences MBand MCrespectively.The rule is that,statesandare both represented as classical bit 0,and statesandas classical bit 1.After that,Bob and Charlie publicly announce MBand MCrespectively.

Step(8):According to SIDBand SIDC,Alice constructs two classical bit sequences MB′and MC′respectively.Under the ideal condition,the two equalities MB′=MBand MC′=MCmust hold if there is no eavesdropping.Therefore,by comparison,Alice believes that there is no eavesdropping and Bob and Charlie are legal if the error rate is low enough.Then the communication continues.Otherwise,it will be stopped.

Step(9):If the controller Charlie permits the receiver Bob to read out the secret message from the sender Alice,he measures every particle in CUwith Zbasis.According to the measurement result,he will form a classical bit string called TCU.The rule is that the measurement resultcorresponds to classical bit 0 whilecorresponds to classical bit 1 respectively.Then Charlie announces the classical bit string TCU.

Step(10):Bob measures every particle in BUwith Zbasis.According to the measurement result,he will form a classical bit string called TBU.The rule is the same as Charlie’s.

Step(11):Alice prepares the secret message M which is expressed as[M11,M21,M12,M22,,M1N,M2N].Similarly,M is divided into two subsequences M1and M2which denote [ M11,M12,,M1N]and [ M21,M22,,M2N]respectively.For convenience,we let Mbe expressed as M1M2.Then Alice encrypts it with TATTAKbit by bit using XOR operation to get E1E2(E1E2= M1M2⊕TATTAK).After that,Alice publishes E1E2.

Step(12):Bob obtains TCaccording to TCUand I DB.That is,TC= IDB⊕TCU.

Step(13):Bob obtains TBaccording to TCand TBU.That is,TB= TBU⊕TC.

Step(14):According to TBand TC,Bob reads out the secret message M1M2by XOR operation from E1E2.That is,M1M2= TBTC⊕E1E2.

In this CQSDC protocol,we can find some obvious drawbacks.Firstly,the security of the identities determines the security of the protocol,because the identities are used to identity authentication as well as eavesdropping check at the same time.Secondly,inder to decrypt the secret message,there is only one kind of measurement is performed on information carrier particles,so there is no error introduced if an eavesdropper happens to make the same measurement on an information carrier particle.

3 Cryptanalysis of the original CQSDC protocol

3.1 Eavesdropping on the identity strings of the receiver and the controller with the SCNO attack

We find that Eve can take the so-called attack strategy,the SCNO attack strategy [Liu,Chen and Liu(2016)] to successfully steal some information of the receiver's identity string()and the controller's identity string().In this strategy,only some selected particles not all the travelling particles are attacked.The detailed idea can be described as follows.At first,an ancilla sequence each of which initially stays inis prepared by Eve.When every even particle in the travel sequence passes by,a CNOT operation is performed on this particle and an ancilla with this particle as the control qubit and the ancilla as the target,whereThen she will manipulate each ancilla to continue to attack.Let us take the case that Eve eavesdrops on

Step(a):Eve prepares an ancilla sequence,and makes each particle of the sequence initially stay in.When the sequenceis transmitted from Alice to Bob in Step(6)of the CQSDC protocol,Eve chooses the even particles to attack.That is,if the particle is in the odd position,Eve just let this particle pass by,but if it is a particle in the even position,Eve captures it,makes one CNOT operation on this particle and an ancilla(Here,Eve lets the particle be the control qubit and the ancilla be the target qubit),and then releases the particle but measures the ancilla with Zbasis.In consequence,she will obtain one classical bit sequence FUaccording to the measurement result.The rule is that:the measurement result 0is expressed by classical bit 0 and measurement resultis expressed by classical bit 1.It is easy to find the Eve's action will not introduce any error.Here we will give the detailed reasons.For one thing,if one bit of I DBis 0,one can easily know that the particle Eve will measure in her attack is a decoy particle which inevitably stays in Z basis in line with Step(5)and Step(6)of the CQSDC protocol,so it can be successfully copied by a CNOT operation without bringing error.For another thing,if one bit of I DBis 1,one can easily know that the particle Eve will measure in her attack is a cluster state particle.According to Step(10),it will be measured with Z basis.Obviously,Eve’s CNOT operation acting on this particle and an ancilla in the statedoes not change the Z basis measurement result on this particle but makes the ancilla has the same measurement result,so measuring the ancilla with Z basis does not introduce error too.

To understand Step(a)more explicitly,an example will be taken.We suppose I DBis a five-bit string“00111”which is the same as that in Fig.1 of the original CQSDC protocol [Nanvakenari and Houshmand(2017)],and IDB,SIDBand BUbe expressed as“ IDB1IDB2IDB3IDB4IDB5”,“ SIDB1SIDB2SIDB3SIDB4SIDB5”,“ BU1BU2BU3BU4BU5”respectively.Obviously,SIDB1and SIDB2are in Z basis while SIDB3,SIDB4and SIDB5are in X basis.Then the sequence BU′can be expressed as“BU1SIDB1BU2SIDB2SIDB3BU3SIDB4BU4SIDB5BU5”.The particles labeled even in this sequence are SIDB1,SIDB2,BU3,BU4,BU5respectively.We have known that SIDB1and SIDB2are in Zbasis,so their states can be copied into the ancillas by CNOT operations.At the same time,we can deduce that BU3,BU4,BU5will be measured with Zbasis by the receiver Bob in Step(10).As we know,a CNOT operation on each of these particles and an ancilla in the state0does not change the Zbasis measurement results on this particles but makes the ancillas has the same measurement results,so there is no error introduced if the ancilla is measured with Zbasis.Therefore,Eve measures the ancillas with Zbasis do not introduce any error.Meanwhile,she gets one corresponding classical sequence FBwhich we express it as“FB1FB2FB3FB4FB5”.One possible case of FBis“01001”.

Step(b):Eve gains the classical string MBafter Bob’s announcement in Step(7).Then She compares the classical strings FBand MB.(We let MBbe expressed as“MB1MB2MB3MB4MB5”).One possible case of MBis“01010”.

i.Eve can immediately deduce that the corresponding bit of I DBis 1(For example,Eve can deduce the fourth and the fifth bits of I DBare 1),if a couple of the corresponding bits from FBand MBare different(In the above example,FB4≠MB4and FB5≠MB5),.Now we explain the reason.If it is 0,then according to the rule to insert decoy particles,we know that Eve has measured the copy of the decoy particle in Zbasis in the SCNO attack.Thus,the two classical bits of FBand MBmust be identical.

ii.Eve indeed cannot simply deduce the definite value of IDB,if a couple of the corresponding bits from FBand MBare identical,but this is of great meaning.In fact,the probability distribution of every bit of I DBis not the same as the initial distribution.For example,if FB=MB,Eve can deduce the probability that I DB=0is 2/3 while the prior probability is 1/2.We can refer to Tab.1 to understand the above rules more unambiguously.From Tab.1,we know that Eve has the probability of 1/4 to gain the precise outcomes which means the corresponding bits of I DBare 1.If MB=FB,there is the probability of 2/3 to deduce I DB=0and the probability of 1/3 to deduce I DB=1; if MB≠FB,then IDB=1.

So,the average quantity of information of every bit of I DBthat Eve can gain(denoting by IEve→IDB)is 0.311.

So far,we have put forward the SCNO attack strategy for Eve to eavesdrop on some information of the receiver’s identity string.Similarly,Eve or Bob can take the same attack strategy to eavesdrop on some information of the controller’s identity string.

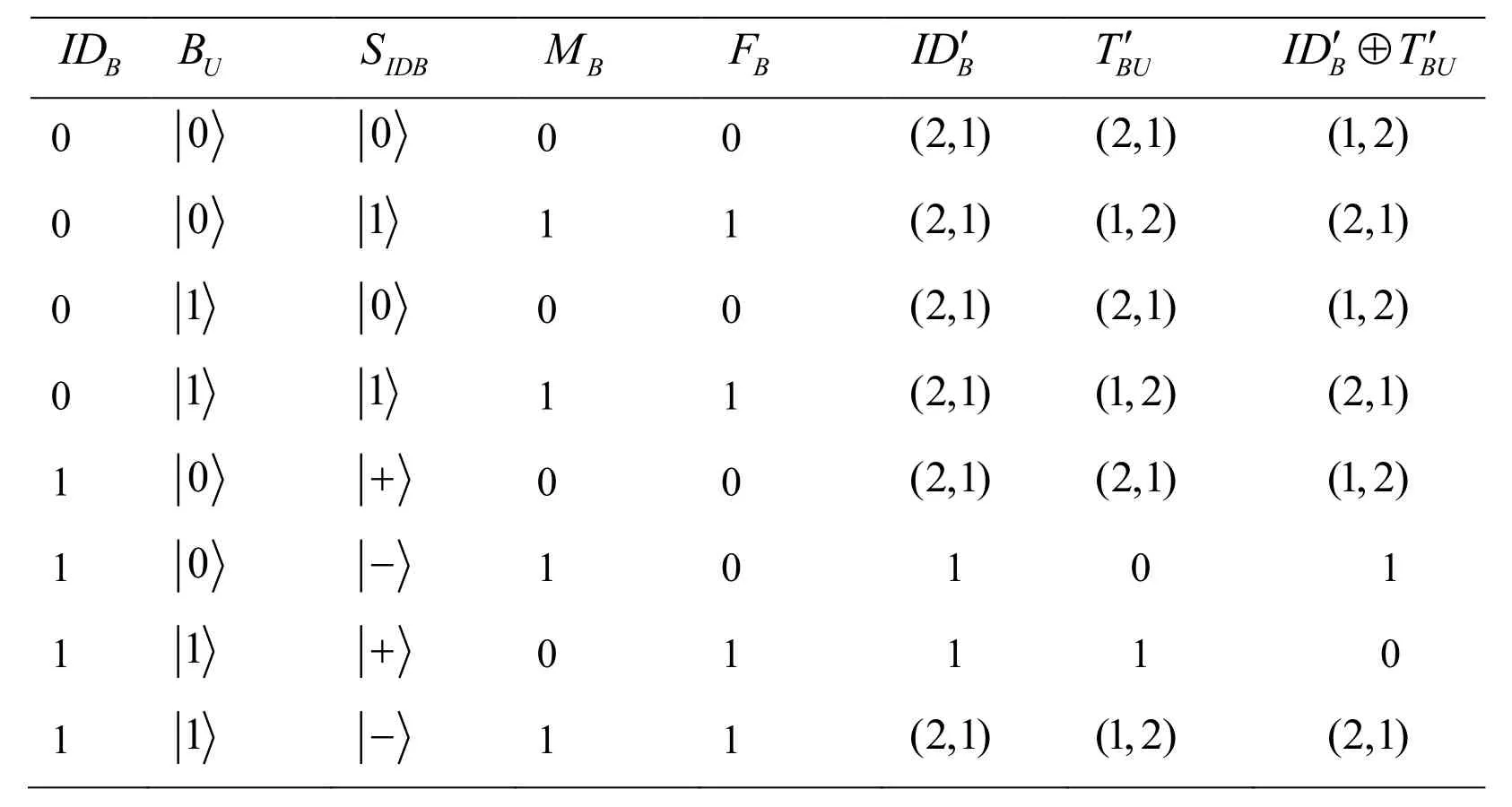
Table 1:Using MBand FBto deduce I DB′,TB′Uand I DB′ ⊕TB′U

IDB′ means the bit string that Eve can be deduced from I DB;

TB′Umeans the bit string that Eve can be deduced from TBU;

(a,b)in the last three columns represents the probability of bit 0 is a/3,and the probability of bit 1 is b/3.

3.2 Eavesdropping on the secret message with the SCNO attack

If Eve wants to get some information of the secret message,she will continue to Step(c).

Step(c):Eve gains TCUfrom Charlie in Step(9),and E1as well as E2from Alice in Step(11).As we know,TB=TAT,TC=TAK, TBU= TB⊕TAK,TCU= TC⊕IDB,E1= M1⊕TATand E2= M2⊕TAK.So,the secret messages M1and M2can be decoded by

and

respectively.Since Eve can get E1and TCUfrom the public classical channel,if she can also gain some information of IDB⊕TBU,she will get some information of M1.If MBFB=00,there is the probability of 1/3 to deduce I DB⊕TBU=0and the probability of 2/3 to deduce I DB⊕TBU=1; If MBFB=11,there is the probability of 2/3 to deduce IDB⊕TBU=0and the probability of 1/3 to deduce IDB⊕TBU=1; If MBFB=10,then I DB⊕TBU=1; If MBFB=01,then I DB⊕TBU=0.There is the probability of 1/4for Eve to get the precise value of I DB⊕TBU.This means that Eve is able to eavesdrop on 1/4of the secret message M1in a determinate way.

Therefore,the average quantity of information of every bit of the secret message M1that Eve can gain(denoting by IEve→M1)is 0.311 if she only intends to acquire some information of M1.

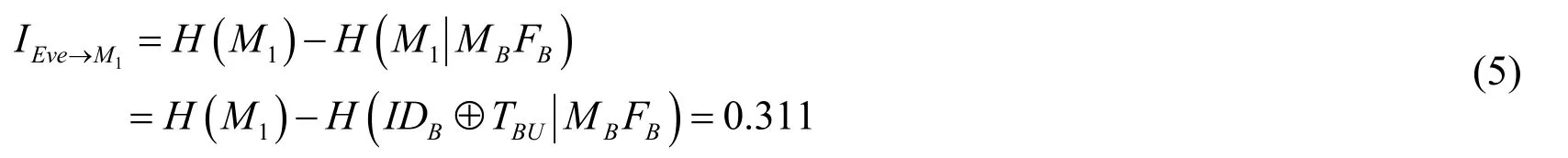
Similarly,Eve can gain 0.311 bit of information about every bit of the secret message M2if she only intends to acquire some information of M2.

If Eve eavesdrops on the secret messages M1and M2together,we find she can get more information than the sum of IEve→M1and IEve→M2.This is because M1and M2are correlated after encryption.If MBFB=00,there is the probability of 1/3 to deduce(I DB,I DB⊕TBU)=(0,0),(I DB,I DB⊕TBU)=(0,1)and(I DB,I DB⊕TBU)=(1,1)respectively; If MBFB=11,there is the probability of 1/3 to deduce(I DB,I DB⊕TBU)=(0,0),(I DB,I DB⊕TBU)=(0,1)and(I DB,I DB⊕TBU)=(1,0)respectively; If MBFB=10,then(I DB,I DB⊕TBU)=(1,1); If MBFB=01,then(I DB,I DB⊕TBU)=(1,0).There is the probability of 1/4for to eavesdrop on the precise value of(I DB,I DB⊕TBU).This means that Eve is able to get 1/4of the secret message M1M2in a determinate way.Actually,the average quantity of information of every couple of the corresponding bits of the secret message M1and M2that Eve can gain(denoting by IEve→M1M2)is 0.811.So far,we have presented the so-called SCNO attack which Eve can take to eavesdrop on some information of the secret message without being detected by the two users,Alice and Bob.

3.3 The receiver eavesdropping on some information of the secret message without the controller’s permission by the SCNO attack

It is well known that a CQSDC protocol must satisfies the basic security requirement that the receiver cannot obtain any information about the secret message without the permission of the controller.However,the original CQSDC protocol does not satisfy this requirement.The receiver Bob indeed can eavesdrop on some information of the secret message without Charlie’s permission if he acts like an eavesdropper as described in the above.Here,Bob’s purpose is to deduce some information of the secret message without Charlie’s permission on basis of some information of TCUis deduced at first.

Since Bob knows IDBand TBU.He also knows E1E2after Alice’s announcement.Therefore,he can deduce some information of the secret message M1M2without Charlie’s permission once he applies the SCNO attack strategy to get some information of TCU.By taking the SCNO attack,we can calculate the average quantity of information of every couple of the corresponding bits of the secret message that Bob can eavesdrop on without Charlie’s permission(denoting by IBob→M1M2).

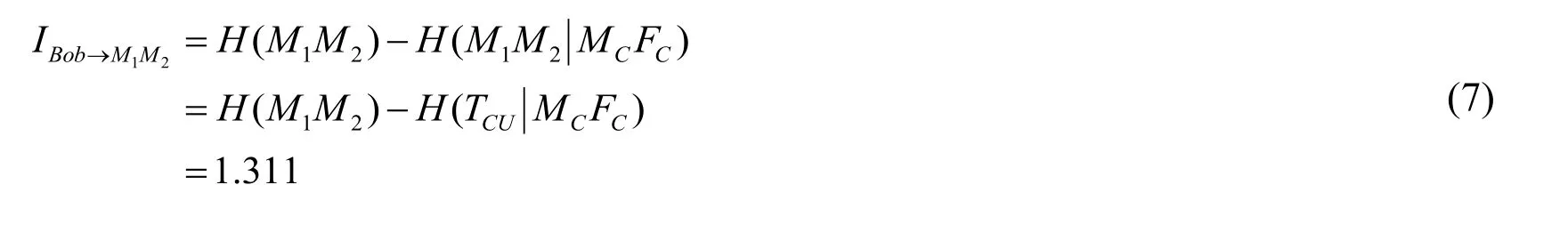
4 Improvement of the original CQSDC protocol

We can summarize the reasons that Eve can successfully attack each even particle in every traveling sequence by the SCNO attack without introducing error is that:These particles are either decoy particles or information carrier particles,but every of them is measured with the same basis,Z basis.This is determined by the rules that Alice prepares the decoy particles and then mixes them into the information carrier particles.In each running of the CQSDC protocol,each identity string is used twice,one for determining the bases of the decoy particles,and the other for determining how the decoy particles are mixed into information carrier particles.This is indeed a drawback.Eve can ingeniously utilize this drawback to take an effective attack but does not introduce any error.To avoid the identity strings to be reused twice in each running,we can change the protocol a little.

Step(R1):Alice prepares an ordered sequence of N number of four particle cluster states,and makes each of them stay in the state.Then,Alice constructs the ordered Band C sequences by particles bnand cnfrom each state respectively.The remaining particles tn andconstruct the ordered A sequence [t1,k1,t2,k2,,tN,kN].For convenience,we also denote the two subsequences [t1,t2,,tN]and [ k1,k2,,kN]by the Atsequence and the Aksequence respectively.

Step(R2):Alice performs the unitary operation U0on the corresponding particle in the C sequence if a bit of I DBis 0,otherwise the unitary operation U1will be performed.In consequence,a new ordered sequence can be obtained.We call it CU.

Step(R3):Alice measures the Asequence in Zbasis and gets an ordered classical bit sequence TAwhich denotes [ TAT1,TAK1,TAT2,TAK2,,TATN,TAKN].Similarly,TAcan divide into two subsequences TATand TAKwhich denote [ TAT1,TAT2,,TATN]and[TAK1,TAK2,,TAKN]respectively.For convenience,we let TAbe expressed as TATTAK.

Step(R4):If a bit of TAKis 0,Alice performs U0on the corresponding particle in the B sequence; otherwise U1is performed.In consequence,a new ordered sequence can be obtained.We call it BU.

Step(R5):In line with IDBand IDC,Alice prepares two ordered sequences with Nqubits,SIDBand SIDCrespectively.The rule to prepare a qubit is that: The i-th qubit of SIDB(SIDC)is prepared in Z basis if the i -th bit of I DB(IDC)is 0; otherwise,it is prepared in Xbasis.

Step(R6):Alice prepares two random bit strings R IDBand R IDC.According to R IDBand R IDC,Alice mixes SIDBand SIDCinto BUand CUto form BU′and CU′respectively.The rule is:Alice places the i -th qubit of SIDB(SIDC)just behind the i-th particle of BU(CU)if the i -th bit of R IDB(R IDC)is 0; or else,the i -th qubit of I DB(IDC)is placed before the i -th particle in BU(CU).After that,Alice transmits BU′and CU′to Bob and Charlie respectively.

Step(R7):After Bob and Charlie receive BU′and CU′,Alice publicly announces the two bit strings R IDBand R IDC.After that,Bob and Charlie extract SIDBand SIDCaccording to R IDBand R IDCrespectively.Then Bob and Charlie measure SIDBand SIDCwith the right bases according to IDBand IDCrespectively.In line with the measurement outcomes,Bob and Charlie respectively construct classical bit sequences MBand MC.The rule is:Classical bit 0 expresses both statesand,and classical bit 1 expresses both statesand.Afterward,Bob and Charlie announce MBand MCrespectively.

Step(R8):In line with SIDBand SIDC,Alice generates two classical bit sequences MB′and MC′respectively.Then MB′is compared with MB,and MC′is compared with MC.Under the ideal condition,the two equalities MB′=MBand MC′=MCmust hold if there is no eavesdropping.Therefore,by comparison,Alice believes that there is no eavesdropping and Bob and Charlie are legal if the error rate is low enough.Then the communication continues.Otherwise,it will be stopped.

Step(R9):If the controller Charlie permits the receiver Bob to read out the secret message from the sender Alice,he measures every particle in CUwith Zbasis.According to the measurement result,he will form a classical bit string called TCU.The rule is that the measurement resultcorresponds to classical bit 0 whilecorresponds to classical bit 1 respectively.Then Charlie announces the classical bit string TCU.

Step(R10):Bob measures every particle in BUwith Zbasis.According to the measurement result,he will form a classical bit string called TBU.The rule is the same as Charlie’s.

Step(R11):Assume that the secret message Alice wants to send is M which expresses as [M11,M21,M12,M22,,M1N,M2N].Similarly,Mis divided into two subsequences M1and M2which denote [ M11,M12,,M1N]and [ M21,M22,,M2N]respectively.For convenience,we let M be expressed as M1M2.Then Alice encryptsit with TATTAKbit by bit using XOR operation to get E1E2(E1E2= M1M2⊕TATTAK).After that,Alice publishes E1E2.

Step(R12):Bob obtains TCaccording to TCUand I DB.That is,TC= IDB⊕TCU.

Step(R13):Bob obtains TBaccording to TCand TBU.That is,TB= TBU⊕TC.

Step(R14):According to TBand TC,Bob reads out the secret message M1M2by XOR operation from E1E2.That is,M1M2= TBTC⊕E1E2.

In the improved protocol,the identity strings are only used once to determine the bases of decoy particles.In addition,the decoy particles which are regularly inserted into the corresponding information carriers according to the identity strings are randomly mixed into the corresponding information carriers.As a result,the particles labeled even in each traveling sequence are not always staying in Z basis or measured by Zbasis.Therefore,if an attacker still takes the SCNO attack strategy,some errors will be inevitably introduced,which will lead to the stopping of the communication before the secret message is transmitted.This indicates that the improved CQSDC protocol is secure.

5 Conclusion

To sum up,the CQSDC with authentication protocol [Nanvakenari and Houshmand(2017)] is cryptanalyzed.We find that some security issues exist in it.By the Eve’s SCNO attack,some information of the receiver’s and the controller’s identity strings can be eavesdropped on without being checked.Thus,she can successfully eavesdrop on some information of the secret message the sender transmits.In addition,the receiver can take the SCNO attack to eavesdrop on some information about the secret message without the controller’s permission.This does not satisfy the basic security requirement of CQSDC.At last,the original CQSDC protocol is improved to a secure one.

Acknowledgement:This work was supported by National Natural Science Foundation of China(Grant No.61502101),the Six Talent Peaks Project of Jiangsu Province(Grant No.XYDXX-003),Scientific Research Foundation of the science and Technology Department of Fujian Province(Grant No.JΚ2015023),and Shangda Li Education Foundation of Jimei University(Grant No.ZC2013010).