A Virtual Puncture Surgery System Based on Multi-Layer Soft Tissue and Force Mesh
2018-12-26XiaoruiZhangJialiDuanLifengZhuandLadislavKavan
Xiaorui Zhang ,Jiali DuanLifeng Zhu and Ladislav Kavan
1Jiangsu Engineering Center of Network Monitoring,Nanjing University of Information Science &Technology,Nanjing,210044,China.
2 School of Instrument Science and Engineering,Southeast University,Nanjing,210096,China.
3 School of Computing,University of Utah,Salt Lake City,UT 84112-9205,USA.
Abstract:Puncture is a common operation in surgery,which involves all kinds of tissue materials with different geometry and mechanical properties.As a new cross-disciplinary research area,Virtual Surgery(VS)makes simulation of soft tissue in puncture operation possible in virtual environment.In this paper,we introduce a VS-based puncture system composed by three-layer soft tissue,simulated with spherical harmonic function(SHF),which is covered with a force mesh,constructed by mass spring model(MSM).The two models are combined together with a parameter of SHF named surface radius,which provides MSM with real-time deformation data needed in force calculation.Meanwhile,force calculation,divided into the surface spring force and the puncture damping force,makes the force presentation better accord to the corresponding tissue characteristics.Moreover,a deformation resumption algorithm is leveraged to simulate the resumption phenomenon of the broken tissue surface.In evaluation experiment,several residents are invited to grades our model along with other four mainstream soft tissue models in terms of 7 different indicators.After the evaluation,the scores are analyzed by a comprehensive weighted grading method.Experiment results show that the proposed model has better performance during puncture operation than other models,and can well simulate surface resumption phenomenon when tissue surface is broken.
Keywords:Puncture simulation,spherical harmonic function,mass spring model,tissue surface resumption,weighted grading evaluation.
1 Introduction
Traditional surgery training is usually performed on soft tissues,like animal tissue,and cadaveric.However,animal tissue is different from human tissue,and cadaveric is of high cost.So,the research on surgery training needs further breakthrough.With the rapid improvement of computation capacity of computers,Virtual Surgery(VS)enables realtime soft tissue simulation in virtual environment,which can greatly shorten training period for surgery training,and reduce training cost for purchasing expensive training materials.The process of soft tissue simulation starts from the medical image data of the soft tissue,like Computed Tomography(CT)scanning data [Yoon,Lee,Ju et al.(2015)]and Magnetic Resonance Imaging(MRI)data [Jiang,Yu,Wang et al.(2016)].Then mathematical model is established on the platforms,like 3DS MAX 2015,and a sort of numerical calculation of deformation and feedback force are carried out with certain algorithms.At last,the operators can operate on the virtual tissue with a computer and a haptic device,such as PHANTOM OMNI,to obtain visual and haptic information synchronously.
Puncture is a common operation in surgery,which involves many kinds of soft tissues,like skin,fat and muscle.Since different soft tissues have different geometry and mechanical properties,they behave differently from each other under puncture operation and need to be separately simulated with VS.The key to simulate soft tissue material is the construction of soft tissue model.Here we introduce four main soft tissue models,i.e.mass-spring model(MSM),finite element model(FEM),boundary element model(BEM),and spherical harmonic function(SHF)model.
MSM is composed of mass nodes that are connected to each other by springs,which represent the internal elastic forces acting between mass nodes of the soft tissue.Such structure makes MSM have advantages in force computation,but it has limited modelling accuracy and stability.Wang et al.[Wang,Chu,Fu et al.(2014)] proposed an improved MSM named unfixed-elasticity mass spring model.In this model,the parameter of each spring is different from each other and will change gradually during deformation.The model cannot present the mechanical response of soft tissue under complex circumstances,e.g.when the needle touches the tissue from different directions,or with different shapes.Tai et al.[Tai,Wei,Zhou et al.(2016)] proposed an immersive needle insertion simulation system for percutaneous surgery with a multi-layer deformable tissue model,where the MSM based force model and algorithm were employed for realistic trocar needle insertion.However,some important parameters,like tissue density,have not been taken into consideration,which may decrease the accuracy of the system.Tang et al.[Tang,Lang,He et al.(2017)] presented a virtual laparoscopic surgery system.In this surgery system,soft tissue deformation was simulated by a special MSM.However,the model is lack of adipose tissue details according to the interaction experiment,which would influence the simulation fidelity.
FEM,composed by connected volumes,can be viewed as a continuous medium,which is a model with high accuracy but large consumption of computational resources.Therefore,FEM is suitable for simulating continuous volumetric organs,especially for the internal structures of them.However,its performance in interactivity during surgical operations is relatively poor due to the large computational consumption.Yeung et al.[Yeung,Crouch and Pothen(2016)] simulated cutting and deformation on a linear elastic model based on FEM,which provided fast updates using augmented matrices.The study focused on linear materials,and the updates of nonlinear materials still need to be accelerated.Townsend et al.[Townsend and Sarigulklijn(2015)] designed a comprehensive procedure with updated Lagrangian finite element formulation to simulate non-linear material models,which could be applied to various biological soft tissue materials.However,this work only offered a theoretical model,but its practical performance remains unknown.
BEM is a developed method after FEM.Different from the basic idea of FEM,BEM only divides elements on the boundary of the defined domain,and then approaches the boundary conditions with functions that satisfy certain equations.Consequently,kinematic equations are transformed into an equation named boundary integral equation,which can be solved to obtain force and deformation information.BEM is suitable for modeling tissues with simple,linear,and isotropic characteristics,such as modelling force on the tip of surgical instruments,when the surgical instruments contact with the soft tissues.However,BEM cannot well simulate complex tissues with rich details,compared with the FEM,especially when there are some changes in topological structure of the simulated tissue.Santiago et al.[Santiago,Trintinalia and Gutierrez(2016)] used BEM to simulate breast and skin lesions.Wang et al.[Wang,Becker,Jones et al.(2006)]employed BEM model to simulate the brain.Three-dimensional(3D)stereoscopic visual equipment and two-handed force feedback devices are utilized to simulate the surgical operations like puncture,pulling,and cutting.
SHF is an equivalent form of Fourier series in 3D modeling [Cheong,Park and Κang(2012)],which can commendably reconstruct the medical image signals,like CT and MRI.The utilization of SHF in soft tissue modeling can improve the calculation efficiency of force and deformation.It is because the level of detail(LOD)of SHF enables the collision detection between instrument and tissue to be rapidly completed.Therefore,the generation time of force feedback is a highlight of this modeling method.However,when calculating the force,the method acquires all-sided parameters [Fang,Bin and Yang(2011)] of soft tissue materials,like density,Young’s modulus,Poisson's ratio,etc.are applicable to the isotropic materials.Moreover,the force computation procedure is relatively complex,which may occupy a large amount of computational resources.
Since puncture procedure requires rapid and accurate force computation,in this paper,we construct a three-layer soft tissue model for puncture simulation by combining advantages of both SHF and MSM in rapid collision detection and accurate force calculation,respectively.In this model,different tissue characteristics are separately presented by applying different tissue texture of skin,fat and muscle and parameters like tissue density and damping coefficient.The soft tissue is simulated based on SHF,whose surface is covered with a force mesh constructed by MSM,to calculate the variable force during the puncture process.In puncture operation,tissue surface would resume to its original position more or less when the needle tip breaks through it.We call the above phenomenon the resumption phenomenon in the puncture operations.In order to simulate the resumption phenomenon,a deformation resumption algorithm based on the shape matching method [Qian,Bai,Yang et al.(2015)] is designed.The main contributions of this work are summarized as follows:
(1)A three-layer soft tissue model is constructed with SHF and MSM.The SHF is utilized to simulate the soft tissue surface,and the MSM is utilized to simulate the force mesh,which makes up for the limitations of SHF in force computation.The two models are combined with a parameter named surface radius,which belongs to SHF and provides deformation data required in the MSM force mesh.The combination can enhance the calculation speed and accuracy of the proposed model.
(2)In order to achieve better force simulation,the calculation of force is divided into surface spring force and puncture damping force.The surface spring force is performed by the MSM force mesh,and the puncture damping force is simulated according to the different tissue characteristics,like tissue density and damping coefficient.
(3)We utilize an improved algorithm,based on shape matching,to simulate the soft tissue surface resumption phenomenon,when the needle tip breaks the tissue surface,which makes the puncture effects more realistic.Its core idea is setting goal positions for all the deformed mass nodes,and each deformed node will move back to its goal position under certain velocity.The goal positions of all the nodes can be obtained by a defined resumption matrix.
The remainder of this paper is organized as follows.Section 2 describes the soft tissue model construction,presents the force model,and demonstrates the deformation algorithm based on the shape matching.Section 3 introduces the experiment environments,shows the puncture process and rendering effects,and carries out an evaluation experiment.In the last section,we make a summary on our work and future work is discussed.
2 Method
Generally,the puncture process involves multiple layers of soft tissues.Therefore,we simulate a three-layer soft tissue model on the proposed system,including skin,fat and muscle.In order to differentiate the performance of soft tissue materials,real soft tissue materials are obtained from medical institutions.According to the real tissue materials,parameters,like thickness,damping coefficient,and spring stiff coefficient,are defined.The proposed puncture system consists of three modules,i.e.the soft tissue model construction,the force model construction and the deformation resumption algorithm.
2.1 Soft Tissue model
The soft tissue model is constructed on the basis of SHF.Skin,fat,and muscle surface,constructed by SHF,respectively,and then the three layers of tissue are combined in the following sequences:Skin the uppermost layer,fat the middle layer,and muscle the lowermost layer.SHF is the solution to the Laplace equation in the form of spherical coordinates,which can be defined by
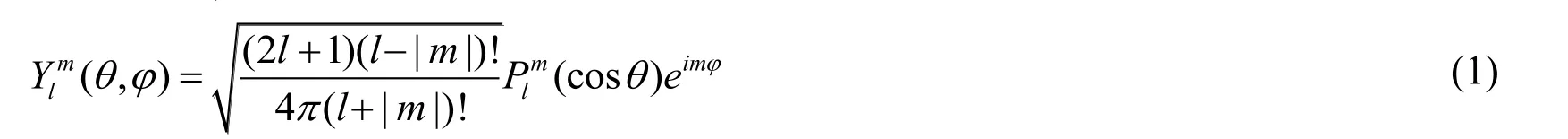
Where l is the level of detail of SHF.l and m are integer,and |m | <l.θand φ represent polar coordinates and coordinate azimuth,and 0<θ<π,0<φ<2π.Plm(x)is associated with Legendre polynomials,which can be defined by

SHF can be used as the basis function to represent spherical surface r(θ,φ).Moreover,the surface can be expressed with three equations based on the parameters θand φ,which expands the SHF to a more general surface.As a result,the objects with any shape can be expressed by SHF functions as the basic functions.
In this work,we construct a three-layer soft tissue surface with SHF.Assuming the soft tissue surface r(θ ,φ)=(x,y,z)T=(x(θ,φ), y(θ,φ), z(θ,φ))T,which represents the surface radius of SHF at point(θ,φ).If r(θ,φ)has been changed,it means there is a collision between the instruments and the soft tissue material.As a result,the deformation of soft tissue can be rapidly obtained according to the change of r(θ,φ).Spherical parametric equations of r(θ,φ)can be expressed by Eqs.(3)and(4).

In Eqs.(3)and(4),Ylm(θ,φ)*is the conjugation ofis the reconstruction coefficient,which includes the shape information of the soft tissue.The key to simulate soft tissue material with SHF is to determine its reconstruction coefficient.
The larger the l is,the more refined the soft tissue is.The growth of lalso causes the increase of algorithm complexity.clmcan be calculated by the least-square fitting approach in Spadaro et al.[Spadaro,Grasso,Cricca et al.(2015)].
2.2 Force model
After building the SHF-based soft tissue model,three meshes constructed by MSM are attached to the surface of each soft tissue layer,which are utilized to make up for the disadvantages of SHF in force computation.The force in the puncture simulation can be divided into two parts.The first part of the force is produced by a specially designed force mesh based on MSM,before the needle breaks through tissue boundary,which is defined as“surface force”.The surface force disappears when the corresponding tissue surface is broken.The second part of the force is the damping force,which is related to the tissue characteristics,needle velocity and puncture depth.Force models of the three kinds of soft tissue materials are shown in the following Tab.1.
In Tab.1,Fs,Ff,Fmare the spring force of skin,fat,and muscle calculated in the first part.his the needle insertion depth with respect to the current tissue boundary.hsand hfrefer to the thickness of skin and fat,and v refers to the needle puncture velocity.ds,dfand dmrefer to damping coefficients of skin,fat,and muscle,respectively.As the needle punctures into these layers,operators will sense the total damping force accumulated by the punctured layers.The force transmission occurs between adjacent layers.The dumping force always exists as long as the needle is moving inside soft tissue.
The computation of surface forces,Fs,Ff,and Fm,is accomplished by the MSM-based force mesh.

Table 1:Force model of the three kinds of soft tissue material
The specially designed MSM-based mesh is built and attached to the SHF-based tissue surface,which will deform synchronously with soft tissue,and produce real-time surface force.Assuming that the surface of the soft tissue is discretized by mass nodes,and surface springs are used to connect the nodes with six adjacent nodes.Any two adjacent nodes are equally spaced,and any three adjacent nodes are connected to form a regular triangle.As a result,a MSM-based force mesh with regular hexagonal topology structure is established,as shown in Fig.1.
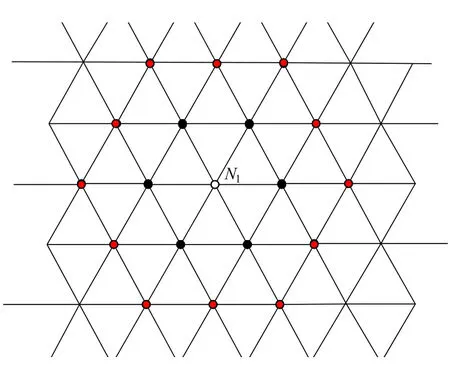
Figure 1:Topological structure of force mesh
As shown in Fig.1,mass nodes in the MSM-based mesh are assigned into a formation of concentric circles distribution,whose center is a white contact node N1.Define the contact node as the first layer of nodes.Six black nodes connected to the contact point are defined as the second layer of nodes.Similarly,twelve red nodes connected to the second layer is the third layer of nodes,and so on.Define w as the maximum concentric circle layer of surface springs,and L as the length of surface spring.L and ware adjusted according to the user need and the tissue texture character.
In order to calculate the surface force,we add virtual springs to the mass node in vertical direction,whose number equals to the number of surface springs.The virtual springs appear and vanish dynamically when soft tissue surface deforms,or when the surface force no longer exists.Fig.2 shows the cross-section of MSM-based mesh with virtual springs.
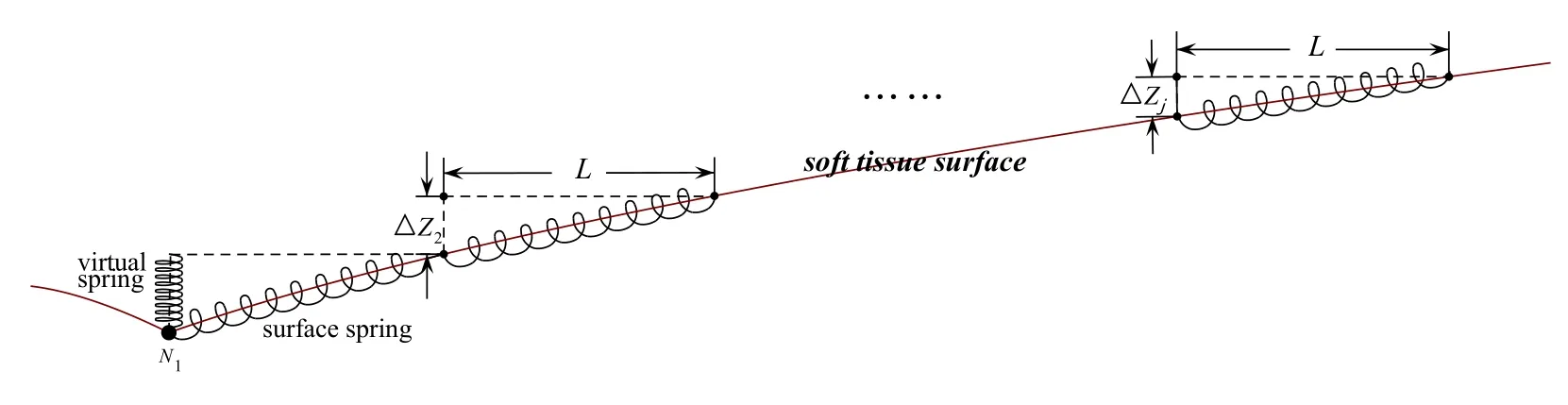
Figure 2:Cross-section of force mesh
As is shown in Fig.2,the external force is applied to node.Assuming j is the number of concentric circles that has deformed.When j = w ,the puncture is at the breaking point,which means the tissue surface will be punctured if the external force increases.The surface force at the breaking point is calculated by

Where K is the stiff coefficient of virtual springs,and Δ Zjis the deformation of node Nj,which can be obtained according to the change of surface radius r(θ,φ)of the corresponding points.
2.3 Deformation resumption algorithm
In the puncture process,the soft tissue surface will return to its original position within a certain extent after tissue surface is broken.In order to express this phenomenon,we adopt a deformation resumption algorithm.The algorithm is based on an improved shape matching algorithm [Qian,Bai,Yang et al.(2015)],whose core idea is to set a goal position giand then let the deformed nodes move to their corresponding giafter surface is broken,as shown in Fig.3.
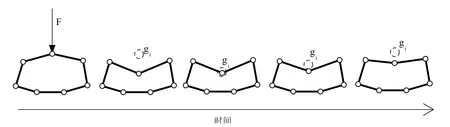
Figure 3:Procedure of the shape matching algorithm
In Fig.3,ig,a deformation resumption matrix A is the key of the deformation resumption algorithm.In order to obtain ig is designed,which records all the current and original positions of the deformed mass nodes and the barycenter of soft tissue.Data in A are updated in real time during the whole puncture simulation.The equation of A is as follows.

Where n is the number of mesh nodes of the soft tissue model,Miis the node mass,piand pi0is the current and original position of every mass nodes i ,pcmandare the current and original position of barycenter of soft tissue.After constructing the deformation resumption matrix A,the goal position giof each deformed mass node can be calculated by

where R is the rotation matrix,and αis the symmetry coefficient.Matrix ATis the transposed matrix of the matrix A.In practice,the deformed nodes will quickly return to its goal position,which is incompatible with real tissue resumption.In order to prevent the soft tissue surface from resuming too quickly,a recovery factor ηiis inserted in the resumption of gi,as is shown in Eq.(8).

According Eq.(8),when ηi=0,the node i will directly move to its goal position gi.When ηi=1,and gi=pi,the node i will stay in its current position.ηris a userdefined parameter that controls the resumption speed of all the deformed nodes.Besides,the SHF-based tissue surface deforms with the MSM-based mesh synchronously.
3 Experiments and results
3.1 Experiments environment
We conduct our experiments on a workstation using Intel Core i7(3 GHz),4 GB RAM,HD7990 graphics card and windows 2007 OS.The haptic device we used in this work is Phantom Omni that allows the operators to touch and operate on virtual objects.Haptic rendering update rate approximate 1 ΚHz and the visual refreshment frequency is 60 Hz.The modified MSM applied to the deformable tissue generates a real-time feedback with the visualization.The software platform consists of VC++2015,3DS MAX 2015,and OPENGL graphics library.Shape information is obtained from medical images and constructed in 3DS MAX 2015.The experiment environment is shown in Fig.4.

Figure 4:Experiment environment
During the simulation,when operators make the PHANTOM OMNI move in the spatial position,the variation signal will be detected by the position sensor of the PHANTOM OMNI.At the same time,the haptic information produced in the puncture simulation will give a response to the operators,so that they can feel the change of force feedback.When operators contact with soft tissue,we will simulate the deformation according to the proposed algorithm.
3.2 Parameters selection and rendering
After establishing the puncture simulation system on the experiment platform,we carried out the puncture simulation on multi-layer soft tissue.According to the related researches [Tai,Wei,Zhou et al.(2016)],the basic parameters of skin,fat and muscle are set as follows.
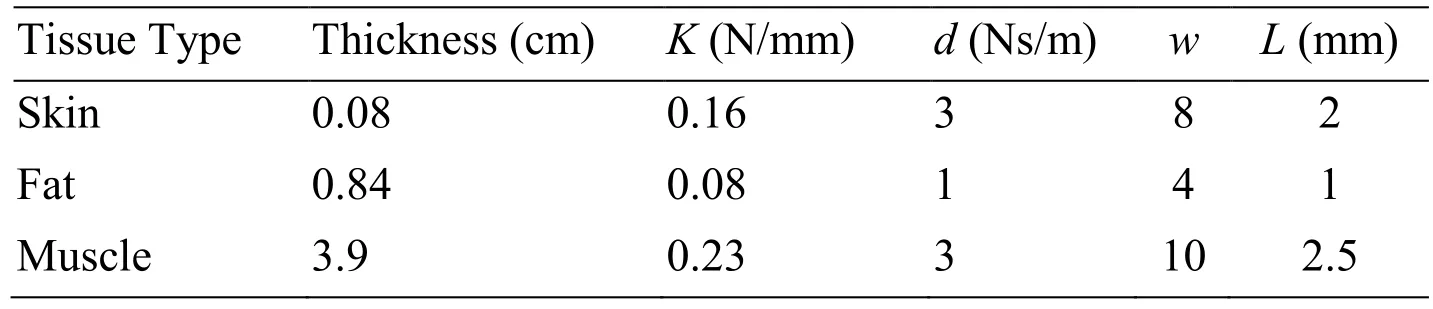
Table 2:Basic parameters
In Tab.2,K is the stiff coefficient of virtual springs,d is the damping coefficient,w is the maximum concentric circle layer of surface springs,and L is the length of surface spring.Regular hexagon mesh is utilized to simulate tissue surface.Six subfigures(i.e.(a)~(c))in Fig.5 show the real-time deformation when the needle is puncturing through the skin,fat and muscle mesh.
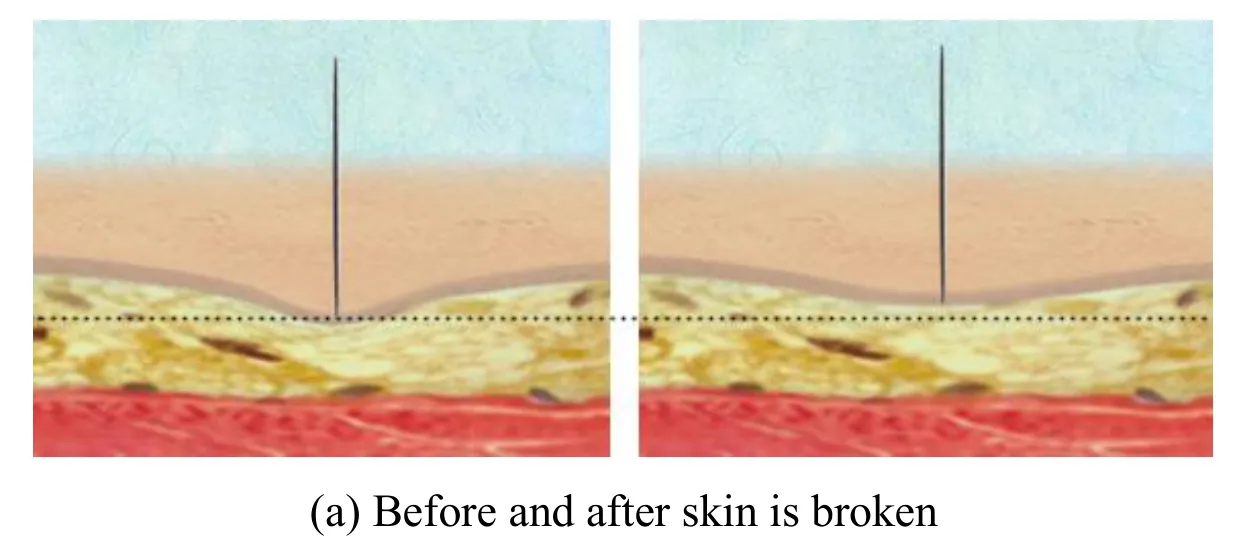
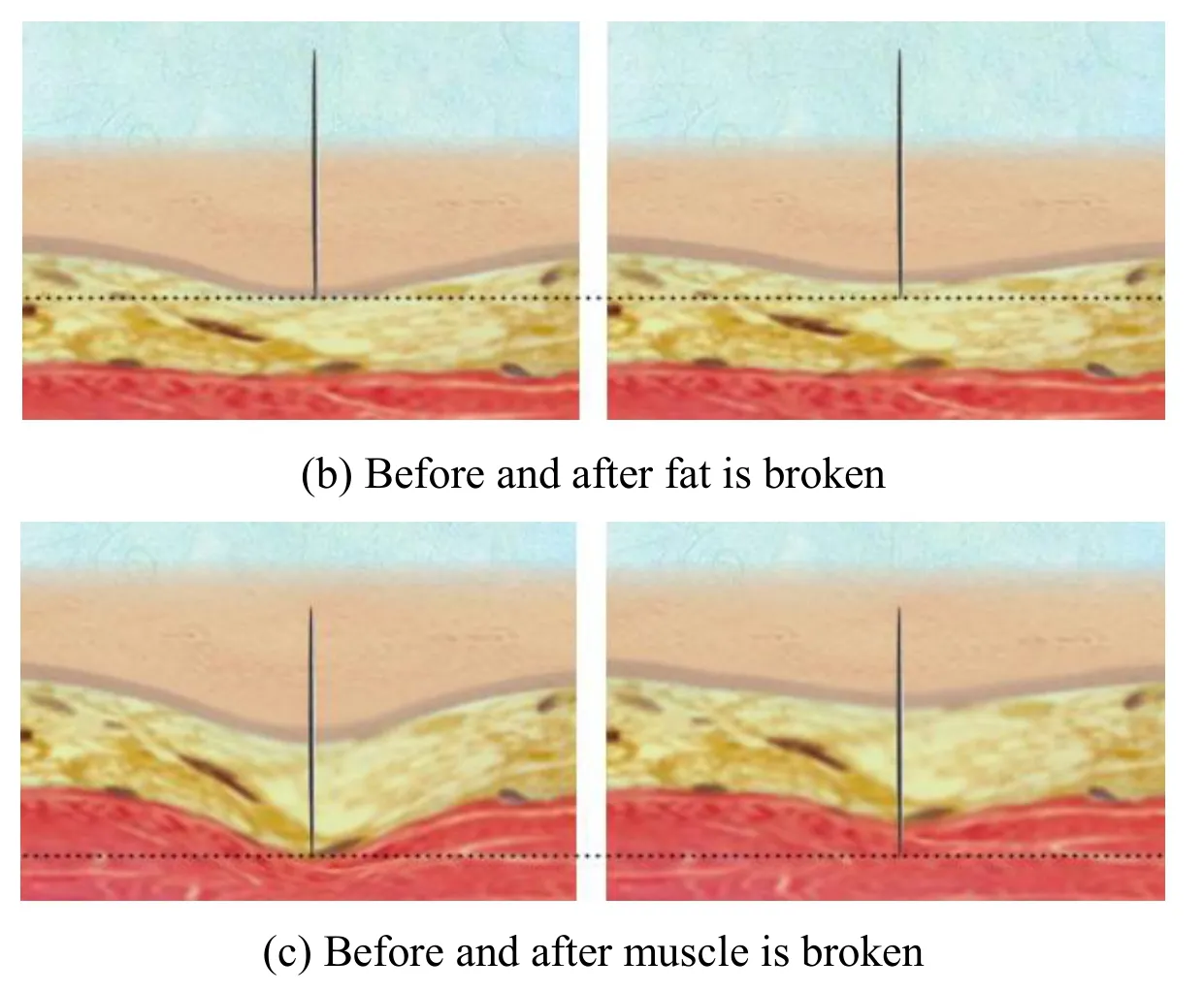
Figure 5:Puncture effects of different tissue
As is shown in Fig.5,the top and thinnest layer of tissue is skin,the middle and yellow layer of tissue is fat,and the bottom and red tissue is muscle.The black dot line is a guideline.The left picture in each group shows right before the needle is breaking through skin,fat and muscle surface.While the right picture shows the resumption phenomenon of different tissue materials simulated by our puncture system when tissue surface is broken.As is shown in the figures,the guideline is based on the surface of tissue when it is intact in the left figures.And when the tissue is broken in the right figures,all three layers of tissue surfaces are the above corresponding guidelines.As a result,the system well presents skin,fat and muscle texture and elasticity,and has good resumption effects when the tissue surface is broken.
3.3 Evaluation experiment
In order to investigate the puncture system performance,several residents in Zhongda Hospital Affiliated to Southeast University are invited,including 11 deputy chief physicians,and 9 chief physicians.The residents were asked to carry out puncture operations with our system and four other puncture systems established with MSM in[Hu and Feng(2017)],FEM in Tang et al.[Tang and Wan(2014)],BEM in Zhu et al.[Zhu and Gu(2012)],and SHF in Fang et al.[Fang and Wu(2011)] respectively.After the operation experiments,residents graded the five systems with the following 7 indicators,i.e.soft tissue texture,force feedback performance,puncture effect,training environment,real-time performance,training effectiveness,and system stability.The full score of the above indicators are 10.
A comprehensive weighted grading method is utilized to deal with the scores marked by the residents,which is current widely used in the evaluation problem with multiple indicators [Han,Zhu,Yan et al.(2016)].The method determines the weight of each indicator according to its importance in the entire test and converts the multipleindicators problem into a single-indicator problem,which makes the evaluation results more convincing and objective.The comprehensive weight of the indicators is the core of the method,which has two major components,including the subjective weight and the objective weight.In this work,since the experienced residents are invited,the subjective weighting method we selected is the Delphi method.Meanwhile,the scores have identical measurement unit,so the mean square error method is selected as the objective weighting method.The basic procedure of the method is as follows.
(1)Assuming that there are i= {1,2,,n}experimental schemes in the multi-index problem,which includes j = {1,2,,m}experimental indicators.The score of each indicator jachieved in each experimental scheme i is recorded as xij.In this work,an experiment scheme refers to one puncture operation operated by a resident on one model,so n= 2 0,m=7.
(2)Determine the subjective weight with Delphi method.Delphi method is a method based on the knowledge and the experience of experts.The standard steps of Delphi method are as follows.
Step 1:Select 10 to 30 experts in the professional field who have both deep theoretical mastery and ample work experience.
Step 2:Send the indicators to be determined,the relevant information,and first-round weighting rules to the experts.The experts are asked to give the weightsα=(α1,α2,,αm)of each indicator independently,and here
Step 3:Reclaim the results,and calculate the average value and standard deviation of each indicator weight in this round.
Step 4:The calculation results in Step 3 will be given to the experts for reference.All the experts are required to modify the weights according to the calculation results.
Step 5:Repeat Steps 3 and 4 until the standard deviation between each indicator weight given by the experts does not exceed the predetermined one.That is,the opinions of experts tend to be basically coincident.
At this time,the average value of each indicator weight is taken as the subjective weights of indicators.In this paper,20 residents coming from First Affiliated Hospital of Nanjing Medical University in Nanjing are selected as the experts.And the predetermined standard deviation is 0.1.The subjective weights of the indicators in each model are the same.According to Delphi method,the subjective weights of the indicators are set as follows.Tissue texture=0.09,force feedback=0.17,puncture effect=0.24,training environment=0.13,real-time performance=0.10,training effectiveness=0.21,and system stability=0.06.
(3)Determine the objective weight with Mean square error method.Mean square error method is an objective weighted method suitable for data with identical measurement unit.The steps are as follows.
Step 1:Calculate the average value of xijthat each indicator jachieved in every experimental scheme i,as is shown in Eq.(9).

Step 2:Calculate the mean square error of xij,as is shown in Eq.(10).

Step 3:Calculate the weight coefficient of each indicator,as is shown in Eq.(11).

Different models have different objective weights,as the Mean square error method is based on the scores of different models marked by residents,who may have a preference on certain models.Thus,different objective weights can reduce the preference on different models.According to the mean square error method,the objective weights of indicators are shown in Tab.3.
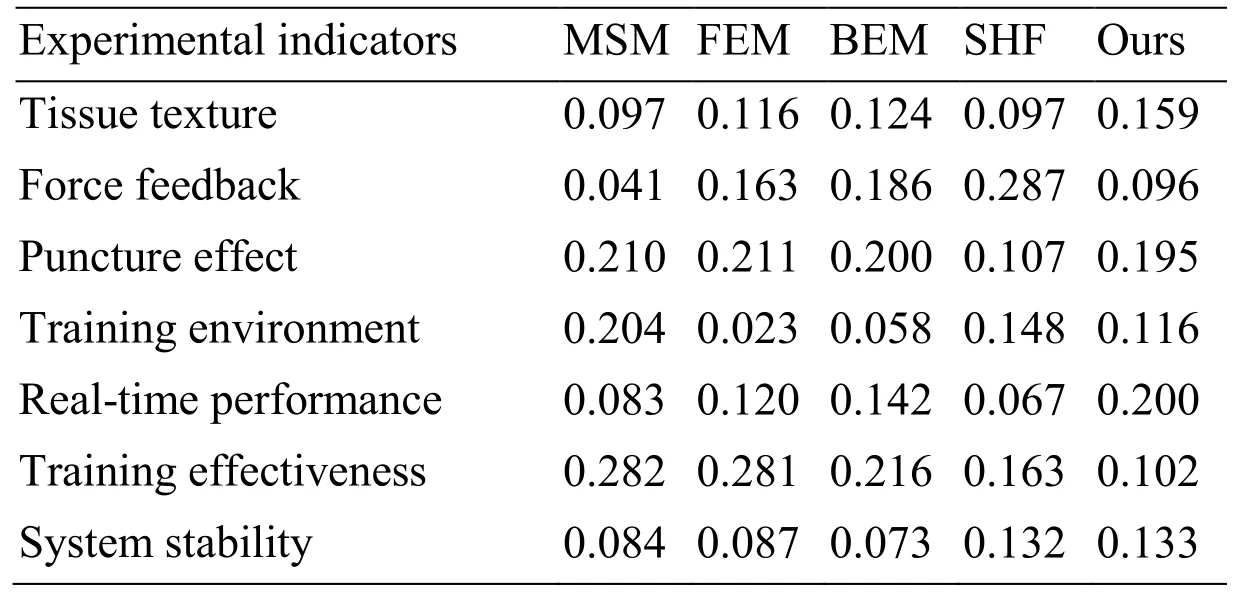
Table 3:Objective weights
(4)Calculate the comprehensive weight and final scores of all models.According to the subjective weights and the objective weights in Tab.3,the comprehensive weights ωjof the experiment indicators are determined.In order to take into account both subjective and objective preferences,and take full advantage of the information provided by the subjective and objective weighting method, the comprehensive weightswhere μis the preference coefficient,0<μ<1,which reflects the subjective and objective preference degree of this work.In this paper,the value of μ is set as 0.4.Therefore,the comprehensive score of experimental schemes i isThe comprehensive scores of five models are shown in Fig.6,where different colored column represents the scores of different residents.
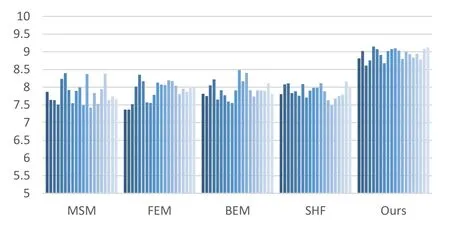
Figure 6:Comprehensive scores of five models
As is shown in Fig.6,the residents generally believe that our puncture system is better than the systems based on the other models in terms of soft tissue texture,force feedback performance,puncture effect,training environment,real-time performance,training effectiveness,and system stability.In general,the average comprehensive score of MSM,FEM,BEM,SHF,and our model are 7.83,7.90,7.93,7.88 and 8.94,respectively.
4 Conclusion and future work
In this paper,we proposed a puncture system composed by a three-layer soft tissue.The tissue surface is simulated with SHF,and the force simulation is accomplished by a MSM-based force mesh.The two models are combined with a concept named surface radius,which is a parameter of SHF and provides deformation data required in the MSM force mesh.As a result,the advantages of rapid collision detection of SHF and accurate force calculation of MSM are combined.In contrast to the existing state-of-the-art puncture systems,the proposed puncture system can well present the tissue resumption phenomenon by the deformation resumption algorithm when the surface is broken.Evaluation experiments based on a multi-index comprehensive weighted grading method shows that our system has better simulation effects than the other models in terms of soft tissue texture,force feedback performance,puncture effect,training environment,realtime performance,training effectiveness,and system stability.For future work,the puncture system can be improved further via simulating the needle with volumetric cylinder,and taking into consideration the contact area and the angle between needle and tissue surface during the force calculation.
Acknowledgement:This work was supported in part by the National Nature Science Foundation of China(No.61502240,61502096,61304205,61773219),Natural Science Foundation of Jiangsu Province(No.BΚ20141002,BΚ20150634).
杂志排行
Computers Materials&Continua的其它文章
- Dynamic Proofs of Retrievability Based on Partitioning-Based Square Root Oblivious RAM
- Phishing Detection with Image Retrieval Based on Improved Texton Correlation Descriptor
- A Method of Identifying Thunderstorm Clouds in Satellite Cloud Image Based on Clustering
- Seed Selection for Data Offloading Based on Social and Interest Graphs
- Analysis and Improvement of an Efficient Controlled Quantum Secure Direct Communication and Authentication Protocol
- A Novel Ensemble Learning Algorithm Based on D-S Evidence Theory for IoT Security
