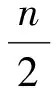BPSK系统对信号载波频率的敏感特性分析
2018-12-26赵琳锋
贾 锐,焦 斌,赵琳锋
(中国洛阳电子装备试验中心,河南 洛阳471003)
BPSK系统对信号载波频率的敏感特性分析
贾 锐,焦 斌,赵琳锋
(中国洛阳电子装备试验中心,河南 洛阳471003)
为研究标准BPSK系统对信号载波频率的敏感特性,讨论了当干扰信号的码速小于或等于期望信号的码速时的情况,以及当2个信号的中心频率相同或不同时,频率偏移对误码率的影响。采用数学建模的方法构建期望信号、干扰信号和噪声模型,得出误码条件概率函数,并基于此,研究信号频率偏移量对标准BPSK接收系统的敏感特性。结果表明,当干信比相同时,在相同的频率偏移下,干扰信号的码速越高,其干扰效果越好;在相同干信比下,接收系统的误码率随着频率偏移量的增大而呈现减小的趋势,且其减小的程度呈现周期性的震荡,震荡的周期仅与期望信号的码速有关;在连续波干扰信号频率偏移量周期变化处,不同码速干扰信号的干扰效果相同。
二进制相移键控系统;敏感特性;误码率;码速;频率偏移量;干信比
0 引言
通信系统是战场C4ISR系统中的重要组成部分,其中数字通信已经成为了其中主要的信息传输方式,二进制相移键控(Binary Phase Shift Keyed,BPSK)具有误码率低、抗干扰性强和信道频带利用率高等特点,在数字通信系统中得到了广泛的应用[1-5]。一些国内外学者对此也做了相关研究,其中最常见的分析方法为将干扰信号等效为BPSK系统接收频带内的噪声,但这种方法并没有考虑到干扰信号是否满足高斯分布,其结果并不精确[6-11]。本文针对干扰信号码速低于或等于期望信号码速的情况下,对标准BPSK数字相干解调系统对BPSK等常见干扰信号的敏感特性开展了定量研究。讨论了标准BPSK系统对BPSK干扰信号主要参数的敏感特性,主要包括期望信号和干扰信号的码速率比、干信比对误码率的影响,以及当2个信号的中心频率不同时,频率偏移对误码率的影响。
1 期望信号、干扰信号和噪声模型
在仅存在加性白高斯噪声(Additive White Gaussian Noise,AWGN),且没有其他干扰的情况下,在不考虑谐波抑制、带外滤波和编码纠错等环节的情况下,采用匹配滤波接收的标准BPSK接收系统的如图1所示。
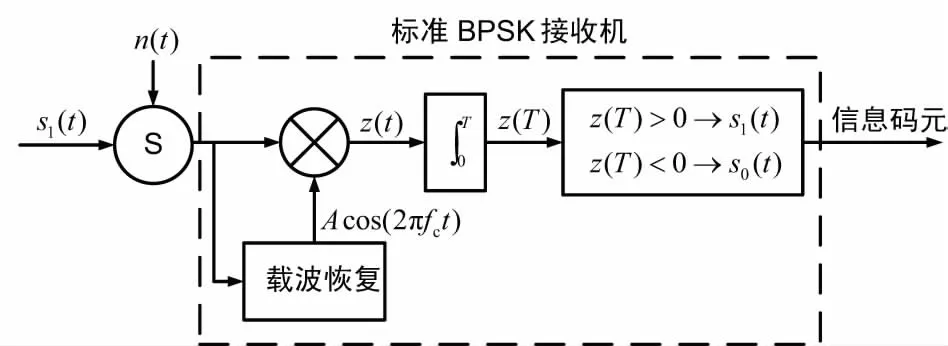
图1 标准BPSK 接收机模型
当噪声为AWGN时,标准BPSK接收系统受到BPSK信号干扰时,接收信号模型可由式(1)给出:

cos[(ωc+δ)t+θ]+nw(t),
(1)
式中,A为期望信号的幅度;AI为干扰信号的幅度;ωc为期望的载波频率;δ为连续波干扰信号频率偏移量;θ为干扰信号的相位;PT(t)为单位高度和持续时间为T的矩形脉冲;T为期望信号的码时间(1/R);TI为干扰信号的码时间(1/RI);τ为位传输时间的偏移量,τ=βmin(T,TI),0< <β<1,dk=±1干扰信号的数据码;nw(t)为均值为0,方差为N0/2的AWGN。
假设RI=2nR,其中n=…,-2,-1,0,1,2,…BPSK干扰信号的和的上限L由相对码速速率决定,
(2)
当n≤0时,在没有干扰信号位发生转换的时候,将存在一些位间隔,在这种情况下,在[0,T]的间隔内,接收信号r(t)中的BPSK干扰信号分量可以简化。检验统计量z(T)为:

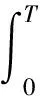
(3)
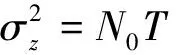
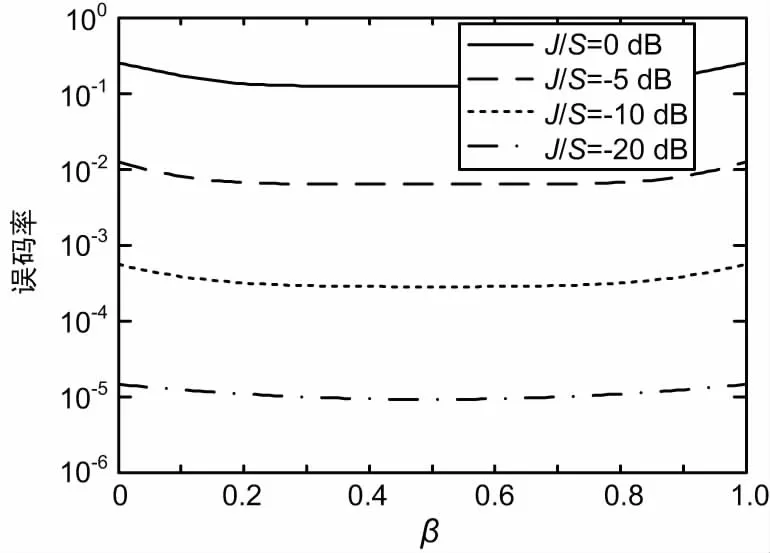
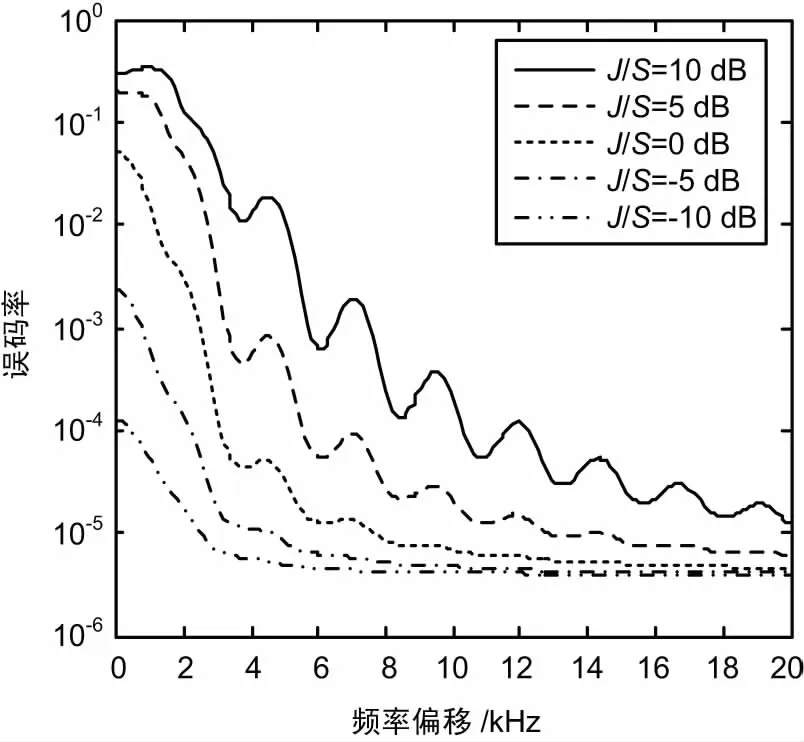
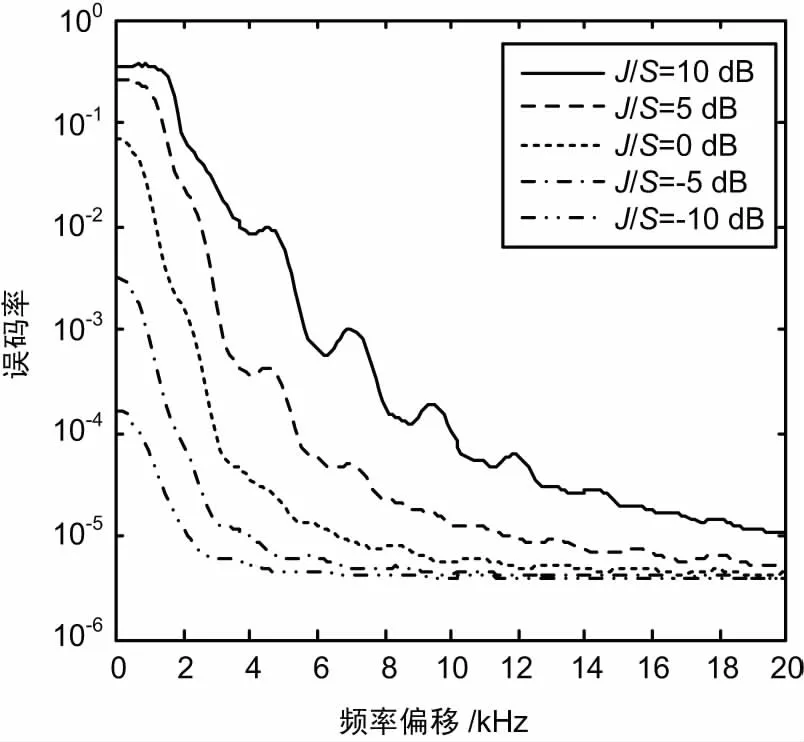
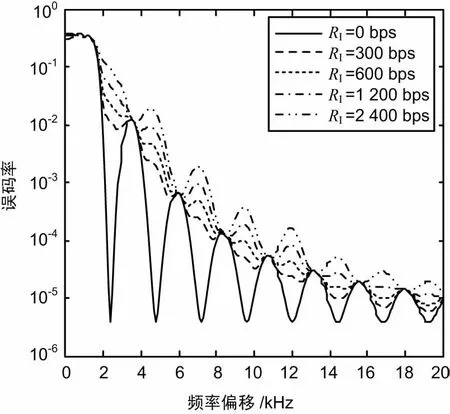
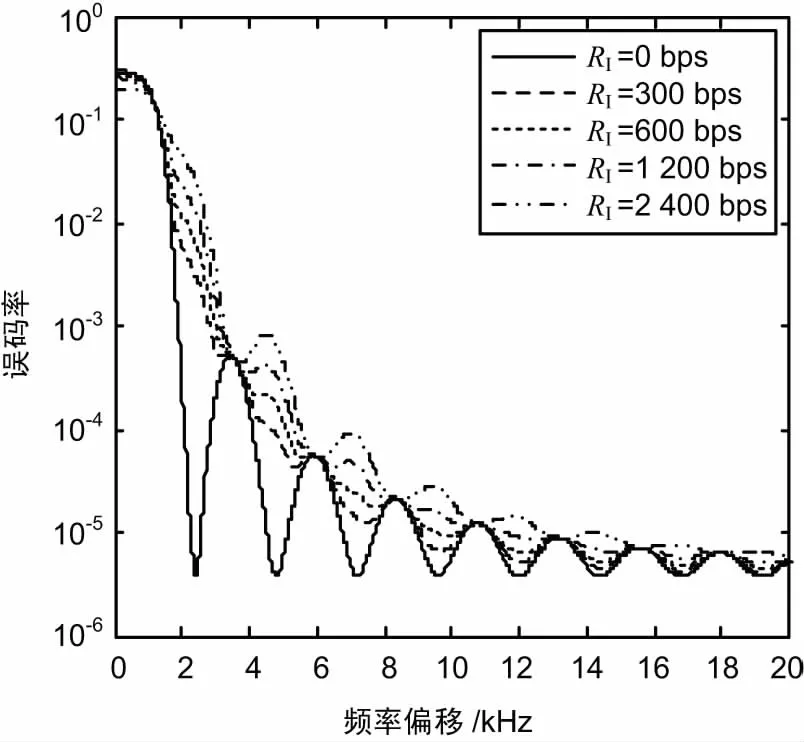
当干扰信号的码速小于或等于期望信号的码速时(RI< r(t) = ±APT(t)cos(ωct)+ AId-1PTI(t+TI-τ)+d0PTI(tI-τ) · cos[(ωc+δ)t+θ]+nw(t)。 (4) 在这种情况下,试验统计量的条件期望值为: (5) 式中, (6) 在给定期望信号当前数据位为+1时,误码的条件概率为: (7) 当期望的信号当前数据位为-1时,误码的条件概率为: (8) 因此,在[0,T]内存在干扰信号位变换时,在给定干扰信号的参数的情况下,误码的条件概率为: (9) 由式(7)和式(8)可知, Pe(+1,AI,δ,τ,θ)=Pe(-1,AI,δ,τ,θ), (10) 因此, Pe(AI,δ,τ,θ)=Pe(+1,AI,δ,τ,θ)= Pe(-1,AI,δ,τ,θ)。 (11) 在多个期望的信号的位间隔的范围内,干扰信号与期望信号发生位变的因子γ为: (12) 令式(11)中的τ=0,可以得到期望信号位变化内不存在干扰信号位变化时的误码的条件概率,其误码率等于连续波干扰信号的结果。一般说,当RI< Pe(AI,δ,τ,θ,γ)=γPe(AI,δ,θ,τ)+(1-γ)Pe(AI,δ,0,θ)。 (13) 与式(1)一样,通过对θ和τ的积分可以得到误码率Pe(AI,δ,γ): (14) 其中假设θ,τ相互独立,且在区间[0,2π][0,T]上分别是均匀分布的。当γ→0时, BPSK干扰信号对标准BPSK通信系统的干扰所产生的误码率,将接近于由相同载波能量的连续波干扰所产生的误码率。 将式(6)取频率偏移量δ趋向于0时的极限, (15) 由于τ=βT,且0< <β<1,则试验统计量的条件期望为: (16) 因此,当在[0,T]内存在干扰信号位变换时,误码的条件概率为: (17) 当在[0,T]内没有干扰信号位变换时,β=0通过将替换为A1,式(17)将简化为连续波干扰。同样当θ=0°或θ=180°时,BPSK系统受到的干扰情况最严重。 定义干信比为:J/S=20lgA1/A。令θ=0°,在J/S为0 dB,-5 dB,-10 dB和-20 dB时,可以计算得到不同干信比情况下,标准BPSK系统受到单个BPSK信号干扰时,信号期望码速为2 400 bps,相位偏移量为0°,频率偏移量为0 Hz,不同干信比情况下,误码率与β之间的关系,如图2所示。 图2 [0,T]内存在单个干扰信号位变换情况时的误码率曲线 由图2可以看出,当β=0.5,干扰信号的位变化发生在[0,T]时间内的最平缓部位,接收系统的误码率将减少到其相应干信比情况下最大误码率的一半。 当信干比J/S为10 dB、5 dB、0 dB、-5 dB和-10 dB时,干扰信号的码速分别为2 400 bps、1 200 bps以及0 bps,系统接收误码率随频率偏移量的变化曲线如图3、图4和图5所示,其中θ和τ分别在区间[0,2π][0,T]内随机分布。 由图可以看出,当BPSK干扰信号的码速等于或小于期望信号的码速时,在相同干信比下,接收系统的误码率随着频率偏移量的增大而呈现减小的趋势,且其减小的程度呈现周期性的震荡;当干扰信号的码速等于0时,经与相关文献对比,其干扰效果与连续波信号的干扰相同。 图3 RI=2 400 bps 图4 RI=1 200 bps 图5 RI=0 bps 为进一步研究标准BPSK接收系统误码率随频率偏移增大变化的特性,计算了在相同干信比情况下,期望信号码速R=2 400 bps,干扰信号码速分别为2 400 bps、1 200 bps、600 bps、300 bps和0 bps时,接收系统的误码率随频率偏移的曲线如图6、图7和图8所示。 图6 J/S=10 dB 图7 J/S=5 dB 图8 J/S=0 dB 综合以上分析,对于标准BPSK接收系统,当受到BPSK干扰时,在干扰信号的码速小于或等于期望信号的码速的情况下,BPSK接收系统对接收信号频率偏移量的敏感特性如下: ① 当干信比相同时,在相同的频率偏移下,干扰信号的码速越高,其干扰效果越好,接收系统的误码率越大; ② 接收系统的误码率随着频率偏移量的增大而呈现减小的趋势,且其减小的程度呈现周期性的震荡,震荡的周期仅与期望信号的码速有关; 需要注意的是,本文是在干扰信号码速都是低于或等于期望信号码速的情况下开展研究的,当干扰信号码速高于期望信号码速时,情况较为复杂,将在下一步开展相关研究。 [1] 刘剑锋.DS/BPSK扩频系统单频干扰方法研究及其仿真实现[J].现代电子技术,2008(1):110-112. [2] 眭惠巧.对BPSK相干接收最佳干扰研究[J].无线电通信技术,2001,27(6):33-34. [3] 方立,匡镜明,吕昕.干扰环境下BPSK接收机跟踪一检测联合性能分析[J].电视技术.2001(3):33-36. [4] 刘志华,高惠敏,宋玉凤.单音信号对BPSK的干扰效果分析[J].无线电工程,2008,38(12):18-21. [5] 郑磊,苏彦,朴延彝,等.单频干扰下BPSK接收性能恶化分析及应用[J].宇航学报,2011,32(1):136-141. [6] GARDNERFM.A BPSK/QPSK Timing-error Detector for Sampled Receivers[J].IEEE Transactions on Communications,1986,34(5):423-429. [7] BOSCOG,CURRI V,CARENA A,et al.On the Performance of Nyquist-WDM Terabit Superchannels Based on PM-BPSK,PM-QPSK,PM-8QAM or PM-16QAM Subcarriers[J].Journal of Lightwave Technology,2011,29(1):53-61. [8] THRAMPOULIDISC,ABBASI E,XU W,et al.Ber Analysis of the Box Relaxation for BPSK Signal Recovery[C]∥IEEE International Conference on Acoustics,2016:2217-2230. [9] ALAGHANS.Cramer-Rao Bounds of SNR Estimates for BPSK and QPSK Modulated Signals[J].IEEE Communications Letters,2001,5(1):10-12. [10] JUMC,KIM IM.Error Performance Analysis Of BPSK Modulation In Physical-Layer Network-Coded Bidirectional Relay Networks[J].IEEE Transactions on Communications,2010,58(10):2770-2775. [11] MELIKYANA,KOEHNLE K,LAUERMANN M,et,al.Plasmonic-organic Hybrid (POH) Modulators for OOK and BPSK Signaling at 40 Gbit/s[J].Optics Express,2015,23(8):9938-9946. SusceptibleCharacteristicsofSignal-carrierFrequencyonBPSKSystem JIA Rui,JIAO Bin,ZHAO Linfeng (LuoyangElectronicEquipmentTestCenter,Luoyang471003,China) In order to research the sensitive characteristic of BPSK system to interference signal.The interference signal with a code rate no more than the expected signal’s code rate,and the influence of frequency deviation on BER (Bit Error Rate) at the equal or different center frequency was investigated in this paper.The noise models of expected signal and interference signal were established to research the sensitive characteristics of interference signal.The results show that with higher code rate,more obvious interference effect can be observed at the same SIR (Signal to Interference Ratio) and frequency deviation.And the BER of receive system would decrease along with the frequency deviation increased at the equal SIR.The decreased level showed cyclical oscillation which cycle was only related to code rate of expected signal.And different code rates have the same interference effect at a periodical frequency deviation. BPSK system;susceptible characteristics;BER;frequency deviation;SIR 2017-08-10 国家自然科学基金资助项目(51277180) 10.3969/j.issn.1003-3106.2018.01.04 贾锐,焦斌,赵琳锋.BPSK系统对信号载波频率的敏感特性分析[J].无线电工程,2018,48(1):17-21.[JIA Rui,JIAO Bin,ZHAO Linfen.Susceptible Characteristics of Signal-carrier Frequency on BPSK System[J].Radio Engineering,2018,48(1):17-21.] TN911.4 A 1003-3106(2018)01-0017-05 贾锐男,(1986—),毕业于陆军工程大学石家庄校区武器系统与应用工程专业,博士,助理研究员。主要研究方向:电磁环境模拟及信号处理。 焦斌男,(1981—),硕士,助理研究员。主要研究方向:通信与信号处理。 赵琳锋男,(1983—),硕士,工程师。主要研究方向:雷达信号处理。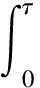

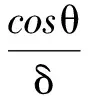
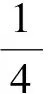
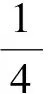
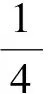
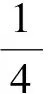
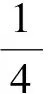
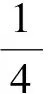
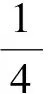
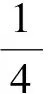
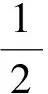
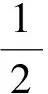
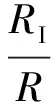
2 干扰信号与期望信号的载波频率相同
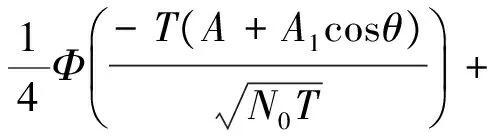
3 干扰信号与期望信号载波频率不同

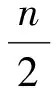

4 结束语