一种多进制LDPC编译码器硬件的实现方法

张亚林，树玉泉，张金涛，魏海涛，张万玉

(1.卫星导航系统与装备技术国家重点实验室， 河北 石家庄 050081;2.河北省卫星导航技术与装备工程技术研究中心，河北 石家庄 050081；3.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；4.陆军北京军代局驻石家庄地区军代室，河北 石家庄050081)

一种多进制LDPC编译码器硬件的实现方法

张亚林1，2,3，树玉泉1，2,3，张金涛1，2，3，魏海涛1，2,3，张万玉4

(1.卫星导航系统与装备技术国家重点实验室， 河北 石家庄 050081;2.河北省卫星导航技术与装备工程技术研究中心，河北 石家庄 050081；3.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；4.陆军北京军代局驻石家庄地区军代室，河北 石家庄050081)

多进制LDPC码比二进制LDPC码性能更加优异，但编译码算法较为复杂，近几年针对复杂的校验节点的更新计算多位学者提出了多种改进算法。提出基于查表法实现直接编码算法，以TMM译码算法为基础，对其译码性能进行Matlab仿真验证，基于硬件实现提出多个关键模块的优化设计方案，最终实现的编译码器资源消耗小、吞吐量大。应用结果表明,该方法实现的编译码器性能与仿真结果一致,设计方案正确、可行。

多进制低密度奇偶校验；查表法；TMM译码算法；现场可编程门阵列

0 引言

LDPC(低密度奇偶校验)码是由Gallager在1962年首次提出来[1]，但由于当时硬件条件限制，一直被忽略，直到1996年MacKay和Neal对它进行重新研究，发现其具有逼近香浓限的优异性能[2]，才重新被人们认识。随后，Davey和MacKay又将二进制LDPC码扩展到多进制LDPC码[3]。研究表明LDPC码在码长较长时，译码性能优于Turbo码[4-5]；多进制LDPC码在纠错能力[6-7]、对高速传输系统的适应性[8-10]方面优于二进制LDPC码。

目前针对多进制LDPC编码的算法主要有直接编码算法、近似下三角编码算法和准循环RA结构编码算法。直接编码算法原理简单，计算复杂度较高，但对校验矩阵无要求；近似下三角编码算法，也叫做RU编码算法，该算法要求校验矩阵具有下三角或可化简为下三角构造，算法复杂度有所减小，但该种结构的码在性能上会有损失[11]；准循环RA结构编码算法利用校验矩阵的准循环结构，进行迭代计算，该算法计算复杂度进一步降低，但要求校验矩阵具有准循环结构[12]。

多进制LDPC译码算法复杂度高，大量计算集中在校验节点的更新，因此目前针对多进制LDPC译码算法的改进主要在校验节点更新算法的简化上。最初Davey和MacKay提出概率域和积译码算法(QSPA)，该算法运算量太大，硬件无法实现；Henk Wymccrsch等人提出对数域和积译码算法(log-SPA)[13]，该算法计算量大幅降低，但硬件仍难以实现；Barnault和Declercq提出了快速傅里叶变换和积算法(FFT-SPA)[14]，该算法利用FFT及IFFT计算校验节点更新中的卷积运算，计算量进一步简化；2007年扩展最小和算法(Extended Min-Sum)被提出[15]，它对和积译码算法(log-SPA)做了近似，使得校验节点的更新只有比较和加法的运算，计算量进一步降低；最大最小算法(Min-Max)[16]在扩展最小和算法的基础上做了进一步改进，将加法运算用比较计算最大置信度代替，避免了加法运算带来的数据位扩展问题，运算量进一步降低；T-EMS(Trellis EMS)算法[17]在扩展最小和(EMS)的基础上额外引入一列最高置信度信息，从而避免了EMS算法和Min-Max算法中前向后向迭代计算，增加了并行度，增大了吞吐速率；TMM(Trellis Min-Max)算法[18-19]进一步简化了T-EMS算法，该算法在计算校验节点时只用到了2个最大置信度信息，并且在配置集计算上使用比较最大值代替了加法运算，同时并不会带来译码性能的损失。

本文所述多进制LDPC码应用背景校验矩阵为64进制、维度为44×88的普通稀疏矩阵，并不具有下三角或准循环结构，因此编码算法采用直接编码算法，提出一种利用查表法计算伽罗华域乘法运算的方法，有效降低了直接编码算法的计算复杂度，提高了编码效率。译码算法在TMM的基础上，对其进行了Matlab仿真验证，并对硬件实现方法进行了进一步优化，提出了多个关键模块的优化设计方案，如整体架构设计、交换网络设计、存储单元设计、比较最小次小值单元设计等。最后以64进制44×88的校验矩阵为例进行编译码的FPGA实现。本文提出的设计方案有效解决了多进制LDPC译码工程实现中资源消耗过大的问题，并在工程实践中得到验证。

1 多进制LDPC码

1.1 直接编码算法原理

假设校验矩阵为：

待编码信息向量为:

x1=x11x12…x1M,

式中，x1i∈GFq,i=1,2…M。

编码后的信息向量为c=x1x2，其中，

x2=x21x22…x2 N-M,x2i∈GFq,

i=1,2…N-M。

(1)

直接编码算法即根据式(1)，由待编码信息和校验矩阵直接计算得出冗余位。流程图如图1所示。

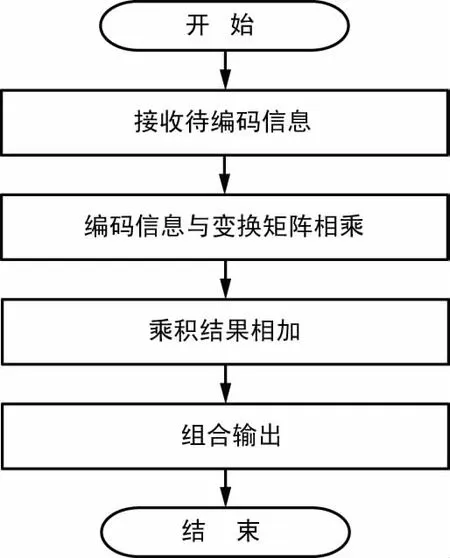
图1 直接编码算法流程

具体步骤如下：① 接收并存储待编码的信息；② 将待编码信息与变换后的校验矩阵在伽罗华域相乘；③ 乘法运算的结果在伽罗华域相加；④ 与待编码信息组合输出编码后的信息比特。

1.2 TMM译码算法原理

多进制LDPC译码算法主体步骤类似于二进制LDPC译码算法，主要包括初始化、迭代更新和输出判决。主要区别在于多进制LDPC译码过程中所涉及到的除概率外的计算均在伽罗华域GFq中进行，另外，在迭代更新过程中由于多进制LDPC每个节点有q个取值的可能，计算复杂度明显增加。

对于校验矩阵HM×N为q=2p进制的LDPC译码具体包括以下步骤。

1.2.1 初始化

初始化的目的是根据接收到的信息完成每个信息对应q个取值的概率。对数操作可将乘除法运算变为加减法运算，显著降低计算量。归一化的目的是使所有的概率取值为非负，为方便后续计算，此时概率越小表示置信度越高。具体计算公式如下:

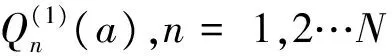
1.2.2 迭代更新

迭代更新包括变量节点更新和校验节点更新,根据初始化信息,通过一定次数的反复迭代计算,最终使变量节点真值位置概率最小,具体计算公式如下:

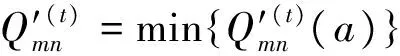
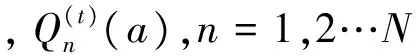
按照m=1,2…M的顺序进行更新，在完成M行计算后表示一次迭代更新结束，重新开始下一次迭代更新，在完成设置次数的迭代更新后，迭代更新步骤完成。

1.2.3 输出判决

根据迭代更新步骤计算的变量节点信息,比较计算最小值所在位置即为译码结果,具体计算公式如下:

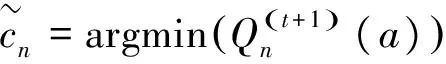
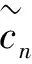
TMM译码算法在计算校验节点更新时通过额外引入一列中间变量，使得校验节点的更新值在每行最小值、次小值和额外引入的值之间选取，整个计算过程只涉及比较和赋值运算，不涉及数据位的扩展，大大简化了计算量，易于硬件实现。TMM的具体计算步骤如下，假设输入为Qmn(a)∈N(m)，为便于表示，这里省略了迭代次数t：

zn=argmina∈GF(q)Qmn(a)∀n∈N(m)

ΔQmnjηj=a+zηj=Qmnj(a)，j=1,…dc

ΔRmnj(a)=ΔQ(a)

ΔRmnj(a)=m2(a)

else

ΔRmnj(a)=m1(a)

end

Rmnja+β+zηj=λ·ΔRmnj(a)，a∈GFq

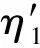
1.3 伽罗华域运算

编译码算法中涉及到的关于位置的运算均在伽罗华域GF(q)中进行，伽罗华域元素可以由本原表示和矢量表示，表1为GF(8)域元素表示法对照表。

伽罗华域中的运算与普通域中运算有所不同，加法运算为矢量表示按位异或；乘法运算中本原表示为0的元素与任何元素相乘仍为0，本原表示非0的元素乘法运算为本原元素的幂次模(2p-1)加。

表1 GF(8)域元素表示法对照表

2 仿真验证

采用Matlab对多进制LDPC直接编码算法及TMM译码算法进行仿真验证。以GF 64 域校验矩阵为H44×88的多进制LDPC译码为例，该校验矩阵行重dc=4，列重dv=2，码长为528 bit。

仿真结果如图2所示，为便于比较引入同样为528 bit码长的二进制LDPC[20]，译码采用BP(和积译码)算法[21-23]。

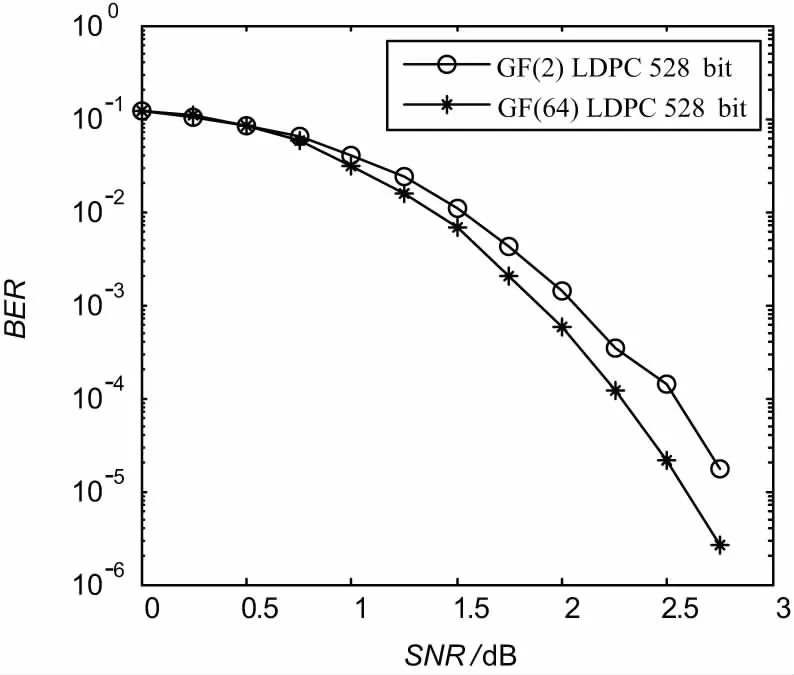
图2 GF(2)与GF(64)LDPC译码性能比较

由仿真结果可以看出，多进制LDPC TMM译码算法原理正确，比同样码长的二进制LDPC性能要好，GF 64 LDPC译码性能优于GF 2 LDPC约0.3 dB。

3 硬件实现

3.1 直接编码算法实现

直接编码算法具体硬件实现整体框图如图3所示，包括存储模块、校验矩阵模块、伽罗华域乘法器、伽罗华域加法器、组合模块和控制模块。

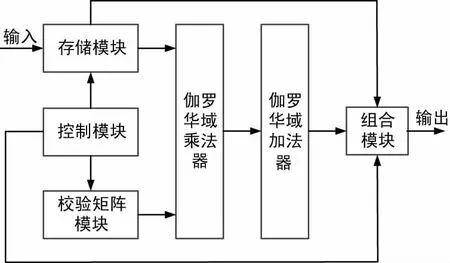
图3 硬件实现整体框图

存储模块用于接收待编码信息，并在控制模块的作用下以p比特为单位存储待编码信息，将待编码信息分别发送至伽罗华域乘法器和组合模块。

校验矩阵模块用于存储对校验矩阵进行变换后得到的矩阵：

将变换后的校验矩阵每一行的值存入一个存储单元，并在控制模块的作用下将各个存储单元中的值发送至伽罗华域乘法器，所述的校验矩阵模块包括M个存储单元。

伽罗华域乘法器用于每次提取各个存储单元中相同列数的一个值，将提取值与待编码信息在伽罗华域相乘，得到乘法运算的结果输出至伽罗华域加法器。

伽罗华域加法器用于将乘法运算的结果在伽罗华域采用按位异或的方法相加，将相加的结果输出至组合模块。

组合模块用于在控制模块的作用下将相加的结果与待编码信息组合，输出编码后的信息。

控制模块用于控制存储模块中输入数据的存储、校验矩阵模块输入伽罗华域乘法器的数据以及编码信息的输出。

伽罗华域乘法器采用查表法实现，实现框图如图4所示，包括第一查找表、第二查找表、模2p-1加模块。xm或hmn为0时，乘法运算结果直接置零；xm和hmn不为0时，将xm和hmn分别减1后作为地址输入第一查找表，第一查找表查找xm和hmn分别减一后的地址所对应的幂次，将查找得到的2个幂次分别输出至模2p-1加模块，模2p-1加模块将2个幂次模2p-1加，将相加的结果作为地址输出至第二查找表，第二查找表查找相加结果的地址所对应的矢量表示，矢量表示结果即为伽罗华域两数相乘的结果，将两数相乘的结果输出。其中，2p表示伽罗华域对应的进制，xm表示第m个待编码信息，hmn表示校验矩阵模块中第m个存储单元中第n个元素。

图4 查表法计算伽罗华域乘法实现

3.2 TMM译码算法实现

TMM译码算法整体实现框图如图5所示，主要包括初始化模块、迭代更新模块、存储模块、输出判决模块和迭代控制模块。

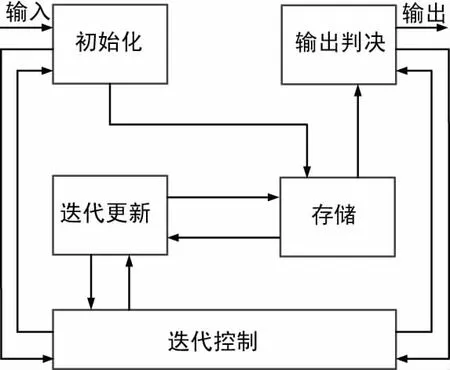
图5 TMM算法整体实现

初始化模块用于在迭代控制模块的作用下接收待译码信息，计算所有输入的待译码信息的后验概率，从所有后验概率中找到最大的后验概率，并根据最大后验概率初始化待译码信息，将初始化后的待译码信息输出至存储模块，并将本模块运行状态报告给迭代控制模块。

迭代更新模块用于在迭代控制模块的作用下从存储模块中读取初始化后的待译码信息、前一次校验节点的迭代更新值和变量节点的迭代更新值，计算本次校验节点及变量节点的迭代更新值，将更新值存入存储模块，并将本模块运行状态报告给迭代控制模块。

输出判决模块用于在迭代控制模块的作用下从存储模块中读取最后一次变量节点的迭代更新值，根据最后一次变量节点的迭代更新值进行译码输出计算，输出译码后的信息，并将本模块运行状态报告迭代控制模块。

存储模块用于存储初始化信息、2组变量节点信息、校验节点信息、校验矩阵信息，接收初始化模块送入的初始化信息，与迭代更新模块进行初始化、变量节点、校验节点、校验矩阵的信息交互，并将最后一次更新的变量节点信息送入输出判决模块。

迭代控制模块用于接收初始化模块、迭代更新模块和输出判决模块的运行状态，并控制初始化模块、迭代更新模块和输出判决模块的工作状态。

迭代更新模块是整个译码算法中最关键的一部分，算法的核心部分都集中在该模块，具体实现框图如图6所示。

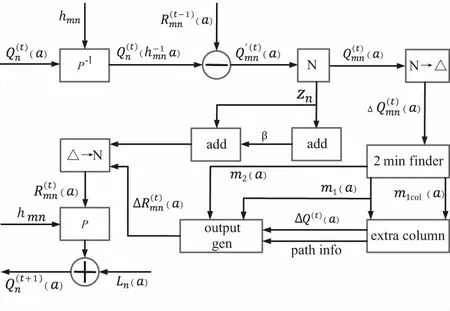
图6 迭代更新模块实现

该模块中与概率有关的运算均在普通域中进行，与位置有关的运算均在伽罗华域中进行。

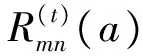
最小值次小值及最小值对应列查找模块(2 min finder)设计2个基本的比较单元，一个比较单元输入为2个被比较值及其所对应列，输出为最小值、次小值及最小值对应的列；另一个比较单元输入为2组最小值、次小值及最小值对应的列，输出为最小值、次小值及最小值对应的列。通过这2种比较器的组合可实现任意多个输入的最小值次小值及最小值对应列信息查找。具体实现框图如图7所示。

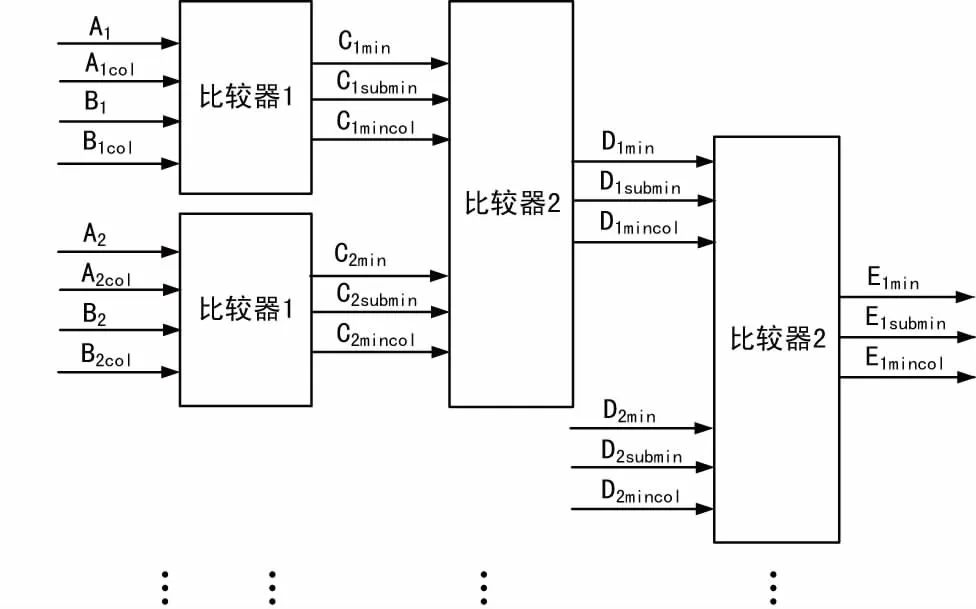
图7 最小值次小值及最小值对应列查找实现

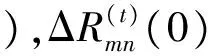
图8 额外列提取计算实现

整个提取过程通过二级比较运算和一级选择运算实现。第一级比较运算通过3个两输入一输出的最大值比较器实现，随后输出至二选一选择器的一个输入口，选择器另一个输入口输入固定最大值，以确保在列信息相等时不会被下一级最小值查找单元选中。选择器通过对应的列信息进行选择，若对应的列信息相等则输出最大值，否则输出2个参与比较的较大的一个，选择器的输出送入最小值查找单元。在计算ΔQ(t)α0时，m1α0不经过第一级比较运算直接输入到最小值查找单元，最小值查找单元找出最小值及其对应的列信息。

4 仿真结果分析

由于多进制LDPC译码算法较为复杂，即使采用计算复杂度最小的TMM算法仍要在资源占用和计算延迟方面权衡考虑，本文在硬件实现时大部分计算以一个节点为最小单位进行串行运算，这样可以最大化地减小资源消耗。在进行m1(a)、m1col(a)、m2(a)以及ΔQ(a)计算时，必须采用并行方法，以一行对应的非零节点为单位进行计算。在缩放系数λ的选择上，通过仿真计算得出λ=0.8时，迭代收敛速度最快，考虑到硬件实现的方便本文选择λ=0.75。

本文以GF 64 域校验矩阵为H44×88的多进制LDPC编译码为例，以altera的stratix IV EP4SE530芯片为平台，对直接编码算法和TMM译码算法进行实现，实现结果编码器硬件资源占用为：逻辑单元(ALUT)：1 763、寄存器(Registers)：5 173、存储单元(Block Memory Bits)：10 736。译码器硬件资源占用为：逻辑单元(ALUT)：71 111、寄存器(Registers)：46 648、存储单元(Block Memory Bits)：202 522。

编译码器实现后Modelsim仿真结果分别如图9和图10所示。编码器只需要7个时钟周期即可得出第一个校验位计算结果，再经过43个系统时钟周期就可以完成整个编码运算。译码器在10次迭代时只需约2 500个时钟周期即可完成从数据输入到译码输出的计算。最终实现的编译码器在相同激励作用下运算结果与Matlab仿真计算结果一致，该编译码器设计正确可行。

图9 编码器Modelsim仿真结果

图10 译码器Modelsim仿真结果

5 结束语

多进制LDPC编码器采用直接编码算法,利用查表法实现伽罗华域乘法运算,原理简单易于实现。译码器虽然采用目前计算复杂度最小的TMM算法，但在硬件实现过程中资源消耗仍较大，尤其是随着进制的增加，每个节点对应的可能性相应增加，存储及逻辑资源消耗变大。本文提出的译码器整体及内部各个模块的实现方案在资源消耗及计算延迟之间进行了折中考虑，根据具体应用需求和硬件平台资源，可通过增加或减小模块并行运算在资源消耗和译码延迟之间统筹考虑。

多进制LDPC码以其优异的性能受到广泛关注，但其复杂的译码算法严重制约了在工程中的应用，本文提出的多进制LDPC编译码方案大大降低了对应用平台的限制，有效拓宽了多进制LDPC的应用场景。

[1] GALLAGER R G.Low-Density Parity-Check Codes[J].IRE Transactions on Information Theory，1962,IT-8(1):21-28.

[2] MACKAY D J C,NEAL R M.Near Shannon Limit Performance of Low Density Parity Check Codes[J].Electronics letters，1996,32(8):1645-1646.

[3] DAVEY M,MACKAY D J C.Low Density Parity Check Codes over GF(2q) [J].IEEE Comunications Letters,1998,2(6):165-167.

[4] 贺琛，韩建兵，贺鹤云.一种性能优于Turbo码的LDPC规则码[J].无线电工程,2008,38(5):21-23.

[5] 张帆，周武旸.一种高速并行的信道编码-LDPC码[J].无线电工程,2005,31(1):48-50.

[6] MACKAY D J C,DAVID J C,DAVEY M.Evaluation of Gallager Codes for Short Block Length and High Rate Applications[C]∥Codes,Systems,and Graphical Models.Springer New York,2001:113-130.

[7] HU X Y,EVANGELOS E.Binary Representation of Cycle Tanner-Graph GF(q) Codes[C]∥Communications,2004 IEEE International Conference on,2004:528-532.

[8] AMIR B,DAVID B.On the Application of LDPC Codes to Arbitrary Discrete-Memoryless Channels[J].IEEE Transactions on Information Theory,2004,50(3):417-438.

[9] LI G,FAIR I J,KRZYMIEN W A.Low-Density Parity-Check Codes for Space-Time Wireless Transmission[J].IEEE Transactions on Wirelses Communications,2006,5(2):312-322.

[10] FENG G,LAJOS H.Low Complexity Non-Binary LDPC and Modulation Schemes Communicating over MIMO Channels[C] ∥Vehicular Technology Conference,2004,VTC2004-Fall,2004 IEEE 60th,2004:1294-1298.

[11] MACKAY D J C,WILSON S T,DAVEY M C.Comparison of Constructions of Irregular Gallager Codes[J].IEEE Transactions on Communications,1999,47(10):1449-1454.

[12] YANG K.Weighted Nonbinary Repeat-Accumulate Codes[J].IEEE Transactions on Information Theory,2004,50(3):527-531.

[13] HENK W,HEIDI S,MARC M.Log-Domain Decoding of LDPC Codes over GF(q)[C] ∥Communications,2004 IEEE International Conference on,2004:772-776.

[14] BARNAULT L,DECLERCQ D.Fast Decoding Algorithm for LDPC over GF(q)[C]∥Information Theory Workshop,IEEE,2003:70-73.

[15] DAVID D,MARC F.Decoding Algorithms for Nonbinary LDPC Codes over GF(q)[J].IEEE Transactions on Communications,2007,55(4):633-643.

[16] VALENTIN S.Min-Max Decoding for Non Binary LDPC Codes[C]∥Information Theory,2008.ISIT 2008.IEEE International Symposium on,2004:960-964.

[17] ERBAO L,DAVID D,KIRAN G,Trellis-Based Extended Min-Sum Algorithm for Non-Binary LDPC Codes and its Hardware Structure[J].IEEE Transactions on Comunications,2013,61(7):2600-2611.

[18] JESUS O L,FRANCISCO G H,DAVID D.Simplified Trellis Min-Max Decoder Architecture for Nonbinary Low-Density Parity-Check Codes[J].IEEE Transactions on Very Large Scale Integration(VLSI) Systems,2015,23(9):1783-1792.

[19] JESUS O L,FRANCISCO G H,CANET M J,et al.A 630 Mbps Non-Binary LDPC Decoder for FPGA[J].IEEE Transactions on Very Large Scale Integration(VLSI) Systems,2015,23(9):1783-1792.

[20] 陈远友.一种用于短猝发通信的LDPC短码设计[J].无线电通信技术,2014,40(1):32-33.

[21] 张亚林，蔚保国，范广伟.IEEE802.16e标准下LDPC码译码性能分析[J].无线电工程,2013,43(11):8-10.

[22] 雷婷，张建志.LDPC编译码算法分析[J].无线电工程,2012,42(10):8-10.

[23] 岳田，裴保臣.LDPC码的几种译码算法比较[J].无线电通信技术,2006,32(4):24-26.

AHardwareImplementationMethodofEncodingandDecodingNon-binaryLDPCCodes

ZHANG Yalin1,2,3,SHU Yuquan1,2,3,ZHANG Jintao1,2,3,WEI Haitao1,2,3,ZHANG Wanyu4

(1.StateKeyLaboratoryofSatelliteNavigationSystemandEquipmentTechnology,Shijiazhuang050081,China;2.SatelliteNavigationTechnologyandEquipmentEngineeringTechnologyResearchCenterofHebeiProvince,Shijiazhuang050081,China;.The54thResearchInstituteofCETC,Shijiazhuang050081,China; 4.MilitaryRepresentativeOfficeinShijiazhuangDistrict,MIlitaryRepresentativeBureauofArmyinBeijing,Shijiazhuang050081,China)

Non-binary LDPC codes have better performance than binary LDPC codes.And because of the complexity of non-binary LDPC codes encoding and decoding algorithms,several scholars proposed some advanced methods in check node processing.The method of direct encoding algorithm based on the lock-up table is proposed.The performance of TMM decoding algorithm is verified according Matlab simulation.And some major module improved design schemes in the hardware implementation are proposed.The encoder and decoder realized in the paper need less resource and have high throughput.According to the application result,the performance of the encoder and decoder using the method is the same with simulation and the design schemes are correct and feasible.

non-binary LDPC;lock-up table method;TMM decoding algorithm;FPGA

2017-01-19

国家自然科学基金资助项目(91638203)

10.3969/j.issn.1003-3106.2018.01.16

张亚林，树玉泉，张金涛，等.一种多进制LDPC编译码器硬件的实现方法[J].无线电工程,2018,48(1):72-79.[ZHANG Yalin,SHU Yuquan,ZHANG Jintao,et al.A Hardware Implementation Method of Encoding and Decoding Non-binary LDPC Codes[J].Radio Engineering,2018,48(1):72-79.]

TN91

A

1003-3106(2018)01-0072-08

张亚林男，(1985—)，毕业于通信与测控技术硬件民通信与信息系统专业，硕士，工程师。主要研究方向：卫星导航。

树玉泉男，(1990—)，硕士，工程师。主要研究方向：卫星导航。

张金涛男，(1979—)，硕士，高级工程师。主要研究方向：卫星导航。

魏海涛男，(1979—)，硕士，高级工程师。主要研究方向：卫星导航。

张万玉男，(1988—)，工程师。主要研究方向：卫星导航。

更正

本刊2017年第47卷第12期第71页“专题技术与工程应用”栏目中，《数字下变频中基于CORDIC算法的NCO设计》一文，“基金项目：国家部委基金资助项目。”更正为“基金项目：国家自然科学基金资助项目(61472136，61772196)；湖南省教育厅科学研究一般项目(15C0103)；湖南省大学生研究性学习和创新性实验项目(601)。”

本刊编辑部