内压对圆筒壳结构模态影响研究
2018-12-26洪良友马斌捷
李 双,李 宁,洪良友,马斌捷,贾 亮
(北京强度环境研究所,北京,100076)
0 引 言
设计航天结构时,结构动特性数据很重要,为控制系统、载荷、POGO、颤振分析提供了基础参考数据,其中控制系统、载荷、颤振分析主要需要参考航天结构整体弯曲模态,POGO主要需要参考航天结构整体轴向模态。为了获得准确的结构动特性数据,当前主要采用试验和仿真计算相结合的办法获取结构的动特性数据。
对于液体运载器,其主体结构通常由多个贮箱与箱间段或级间段组成,且贮箱可能占有主导地位。在飞行过程中或者在模态试验时,贮箱内部一般都保持一定的压力,其对结构整体模态的影响,是动特性数据获取时,需要重点考虑的问题之一。
实际上,箭体或弹体的贮箱是一个圆筒壳结构,对于圆筒壳,理论上可以写出动力学微分方程,但是无法得出解析解,只能通过数值迭代拟合给出数值解[1]。
当前实际工程应用中分析箭体或弹体整体弯曲模态时,方法之一是将整个箭体或弹体简化为一根梁,另一种方法则是采用三维梁-壳模型,其中前者只能反映箭体结构的整体模态,而后者除了能反映整体弯曲模态外,还可以反映壳体的局部模态。但就这两种方法都能反映箭体结构的整体弯曲模态来说,结果会有何差别和一致性,其中第2种采用三维梁-壳模型的方法,贮箱内是否充内压结果又有何差别,一直是航天工程领域关注的问题。
通过梁模型研究全箭的动特性时,为考虑贮箱内压对整体弯曲模态的影响,本文对梁在有、无轴向力作用下相关理论公式进行了推导得出了梁在有、无轴向力作用下的解析解。并通过一个简支梁模型有限元分析进行验证。
采用三维梁-壳模型研究全箭的动特性时,为考虑贮箱内压对于圆筒壳结构整体弯曲模态的影响,由于无法给出解析解,通过一个理想的圆筒壳有限元分析进行了研究。
采用三维梁-壳模型研究全箭的动特性时,对于圆筒壳结构的局部壳体呼吸模态,当前实际工程应用中没有直接的简化方法,但其理论机理与平板模态相同。基于了解圆筒壳结构充内压和无内压壳体呼吸模态关系的目的,本文对平板在有无面内拉力作用下相关理论公式进行了推导,定性的说明了贮箱内压对壳体呼吸模态的影响。
通过对理想的圆筒壳结构自由-自由状态充内压和无内压时的模态进行分析研究,得出了一些规律之后,又进一步对某型号含贮箱的局部芯级圆筒壳结构实例建立了有限元模型,将自由-自由状态充内压和无内压时的模态进行了研究,最后,结合理论公式和数值分析结果,给出了关于内压对箭体动特性影响的一些规律,可供设计与试验时参考。
1 内压影响的理论研究
1.1 轴力对梁结构整体弯曲模态固有频率的影响
由于圆筒壳结构动力学微分方程没有解析解,当前实际工程应用中分析箭体或弹体整体弯曲模态时,方法之一是将整个箭体或弹体简化为一根梁,为了解贮箱充内压与无内压状态用梁简化时弯曲模态固有频率之间的关系,本文对一个简支梁有轴向拉力和无轴向拉力作用的固有频率之间的关系[2]进行研究,简支梁有轴向拉力0T作用的示意如图1所示。
简支梁有轴向拉力0T作用的弯曲模态固有频率如下式:
当00T=,即无轴向拉力时梁的弯曲模态固有频率为下式:
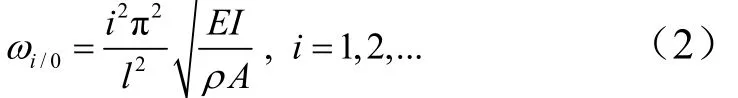
式中iω为简支梁有轴向拉力0T作用的弯曲模态固有频率;/0iω为简支梁无轴向拉力时的弯曲模态固有频率;E为梁材料弹性模量;I为梁截面惯性矩;A为梁截面面积;ρ为梁材料密度;l为梁长度;i为模态阶次。
由式(1)和式(2)可得出简支梁有轴向拉力和无轴向拉力作用的弯曲模态固有频率的关系为
a)当梁受拉时轴力 T0使梁弯曲频率增加,当梁受压时轴力 T0使梁弯曲频率降低;
b)随着模态阶次的增加轴力 T0的影响减弱;
c)当轴力 T0远小于轴向压杆欧拉临界压力时可不考虑轴力对弯曲模态的影响。
1.2 内压对圆筒壳结构壳体呼吸模态固有频率的影响
由于圆筒壳结构动力学微分方程没有解析解,但就内压对壳体呼吸模态固有频率的影响来说,理论机理与面内拉力对一个四边简支平板模态频率的影响是一致的,本文采用一个四边简支的平板有面内拉力(两个拉力,一个剪力)和无面内拉力作用时模态固有频率之间的关系[3~8]来类比定性说明贮箱圆筒壳结构充内压和无内压时壳体呼吸模态固有频率的关系。
四边简支平板有面内拉力示意,如图2所示(为了示图清晰,图中只画出了x轴方向的拉力)。
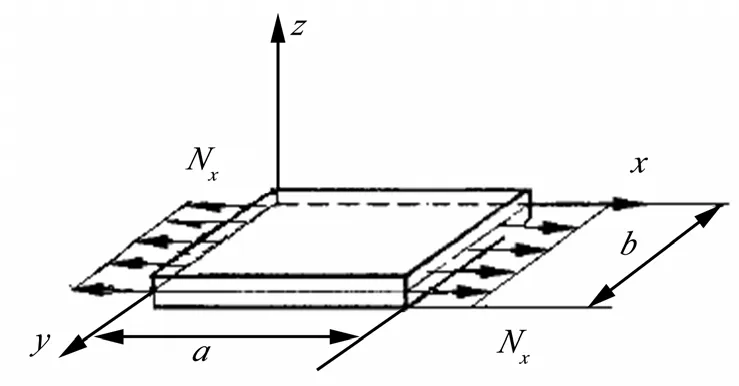
图2 四边简支平板有面内拉力示意Fig.2 Four Sides Simply Supported Plate Imposed Plane InternalTension Load
四边简支平板有面内拉力作用时模态固有频率如下式:
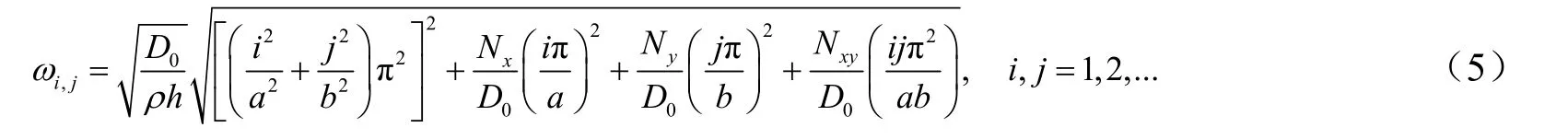
式中 ωi,j为四边简支平板有面内拉力作用时模态固有频率;Nx为作用于与x轴垂直的端面上、方向与x轴一致、沿y轴单位长度的线压力; Ny为作用于与y轴垂直的端面上、方向与y轴一致、沿x轴单位长度的线压力;Nxy为作用于平板侧面的的剪力;D0为平板抗弯刚度,E为平板材料弹性模量;µ为平板材料泊松比;h为平板厚度;a为平板x轴向长度;b为平板y轴向长度;i为板振型包含的x轴方向的半波数;j为板振型包含的y轴方向的半波数。
当 Nx=0, Ny=0, Nxy=0,即无面内拉力,无剪力时平板模态固有频率为下式:
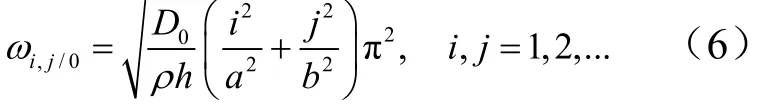
由式(5)和式(6)可得出四端简支平板有面内拉力作用和无面内拉力作用时模态固有频率之间的关系如下式:


式(7)说明:四端简支平板有面内拉力作用相对于无面内拉力作用时对应模态固有频率是增加的。充内压和无内压圆筒壳结构壳体呼吸模态固有频率之间的关系与式(7)类似。
对于充内压和无充内压圆筒壳结构壳体模态固有频率的关系,式(7)中 Nx类比为贮箱环向截面上、方向与环向一致、沿轴向单位长度的线压力,Nx= pR,Ny类比为贮箱轴向截面上、方向与轴向一致、沿环向单位长度的线压力, Ny= pR/2,其中,p为贮箱内压,R为贮箱半径;在这里,将式(6)中代表平板y轴向长度的b类比为贮箱长度; D0为贮箱薄壳抗弯刚度。
2 理想模型验证
为验证理论公式,本文采用一个理想圆筒壳进行验证,其中圆筒壳半径R=0.5 m,长度l=20 m,壁厚度h=0.01 m,材料弹性模量E=70 GPa,泊松比µ=0.3,屈服极限sσ=390 MPa,采用有限元方法分析。
2.1 简支状态理想圆筒壳模型分析
为考察圆筒壳结构充内压和无内压弯曲固有频率的关系是否与梁类似符合式(4),分别采用梁单元和壳单元对该圆筒壳进行建模,边界条件为两端简支。梁单元模拟模型分析结果如表1所示。简支边界理想圆筒壳模型分析结果列于表2。
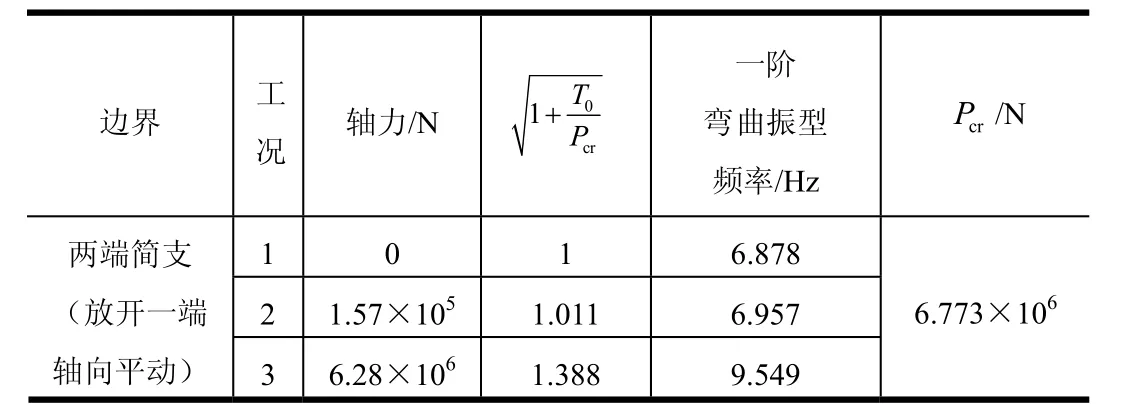
表1 梁单元模拟模型分析结果Tab.1 Analysis Result of Beam Element Simulation Model
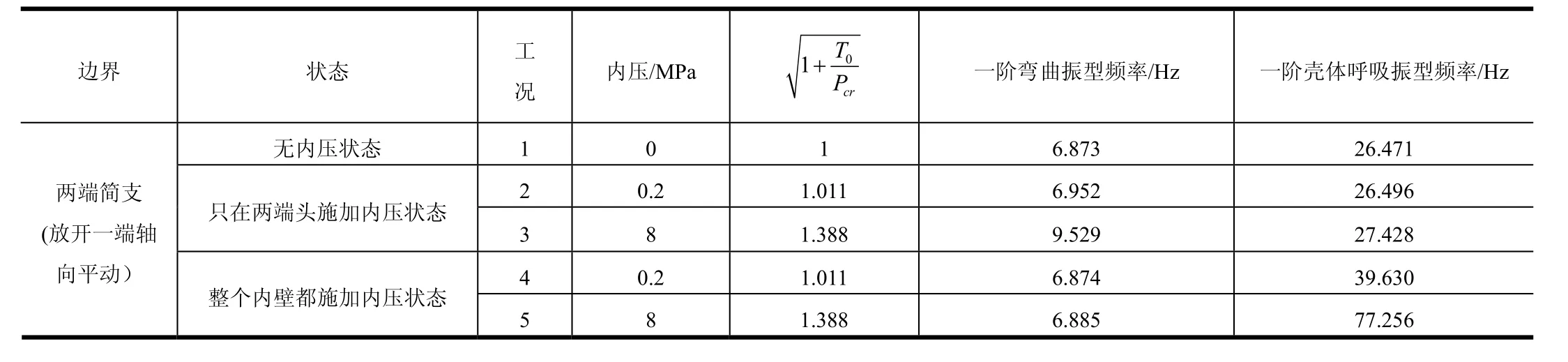
表2 简支边界理想圆筒壳模型分析结果Tab.2 Analysis Result of Idealistic Simply Supported Boundary Cylinder Shell Model
从表1分析结果可看出梁单元模拟模型有无轴力状态的频率关系符合式(4)。从表2结果可看出:
a)用shell壳单元模拟圆筒壳无内压状态一阶弯曲频率与用梁单元模拟无轴力状态一阶弯曲频率基本相同。
b)用 shell壳单元模拟圆筒壳,只在两端头施加内压状态一阶弯曲频率与表 1用梁单元模拟,施加相同的轴力一阶弯曲频率基本相同,且只在两端头施加内压状态与无内压状态一阶弯曲频率的关系与用梁单元模拟结果一样都符合式(4)。
c)用 shell壳单元模拟圆筒壳,只在两端头施加内压状态与无内压状态一阶壳体呼吸模态频率基本不变。这个规律主要原因是只在两端头施加内压时与用梁单元模拟时圆筒壳应力状态类似都是单向轴向应力状态。
d)用 shell壳单元模拟圆筒壳,整个内壁都施加内压时,充内压状态与无内压状态一阶弯曲频率基本不变,这个规律与梁模型施加轴力状态不一致,主要原因是圆筒壳内压状态下,结构上存在环向应力产生的应变,由于泊松比效应,该应变对轴向应变也产生影响,从而影响整个结构的弹性势能,导致充内压状态整体弯曲频率几乎不变。
e)整个内壁都施加内压状态与无内压状态一阶壳体呼吸模态频率增大较多。
2.2 自由-自由状态理想圆筒壳模型分析
自由-自由边界理想圆筒壳一阶弯曲模态频率与内压的关系曲线如图3所示,自由-自由状态理想圆筒壳一阶壳体呼吸模态频率与内压的关系曲线如图4所示。
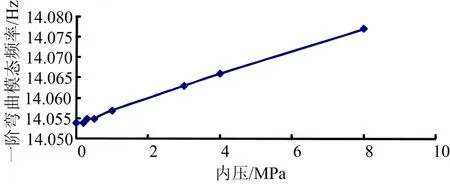
图3 自由-自由边界理想圆筒壳一阶弯曲模态频率与内压关系Fig.3 Relationship of Free-free Boundary Idealistic Cylinder Shell First-order Bending Mode Frequency with Inner Pressure
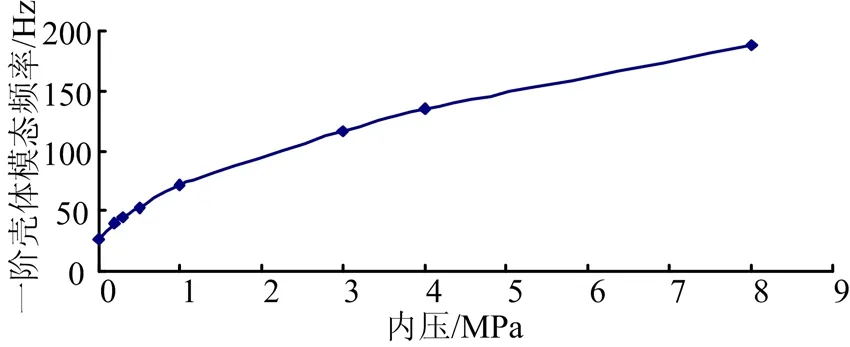
图4 自由-自由状态理想圆筒壳一阶壳体呼吸模态频率与内压关系Fig.4 Relationship of Free-free Boundary Idealistic Cylinder Shell First-order Shell Breathe Mode Frequency with Inner Pressure
从图3和图4可看出自由-自由状态理想圆筒壳模型分析结果符合 2.1中(d)和(e)结论,即用 shell壳单元模拟圆筒壳,整个内壁都施加内压时,施加内压状态与无内压状态一阶弯曲频率基本不变,施加内压状态与无内压状态一阶壳体呼吸模态频率增大较多。
3 实际结构计算
本文采用的实例模型是某型号的部分含有贮箱的芯级结构,其中贮箱半径R=2.5 m,长度l=17.3 m,贮箱壁厚度h=0.0038 m,贮箱材料弹性模量E=70 GPa,泊松比µ=0.3,屈服极限σs=390 MPa。
3.1 理论方法估算分析
由于薄壁圆筒壳结构无法给出模态固有频率的解析解,根据2.1理想圆筒壳模型验证所得出的结论,这个实例贮箱内部充内压时相当于整个内壁都施加内压工况。
3.1.1 实例模型充内压和无内压时弯曲模态固有频率之间的关系
根据2.1的结论(d),这个实例充内压与无内压状态弯曲模态频率相比,由于有环向应力的影响,应是变化不大。
3.1.2 实例模型充内压和非充内压时壳体呼吸模态固有频率之间的关系
根据式(8),当 i =1, j=1时:
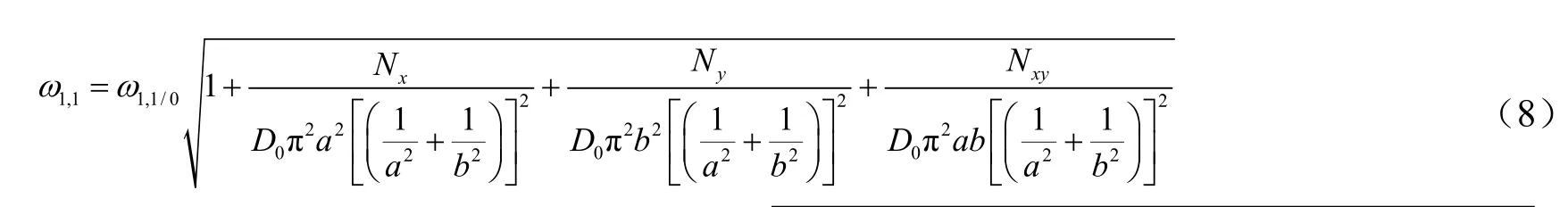

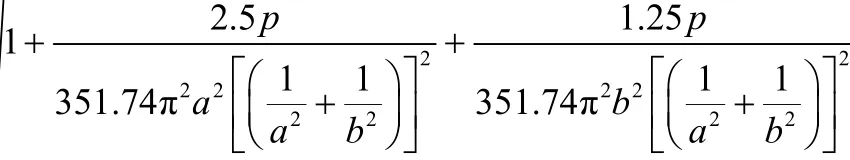
大于1时就可定性地说明1,1ω与1,1/0ω相比是增大的。
3.2 有限元方法分析
3.2.1 动力学模型建模
有限元方法分析,建模时蒙皮采用shell壳单元模拟,纵向和横向加筋采用梁单元模拟,有限元模型如图5所示。

图5 有限元模型Fig.5 Finite Element Model
3.2.2 求解分析
利用Abaqus软件分析求解,分析工况列于表3。选取分析工况时,原则是贮箱最大应力不超过材料屈服极限,因为如果内压过大贮箱最大应力超过了屈服极限,实际工程中不会有这样的工况出现。

表3 分析工况Tab.3 Analysis Case
3.2.3 结果分析比较
实例分析结果列于表4。

表4 实例分析结果Tab.4 Analysis Result of Instance
表4结果可看出,充内压状态与无内压状态之间的频率关系符合2.1节中第(4)和(5)条结论即充内压状态与无内压状态一阶弯曲频率基本不变,施加内压状态与无内压状态一阶壳体呼吸模态频率增大较多。
4 结 论
比较表1中梁模型验证结果、表2中理想圆筒壳模型验证结果和表4中实例分析结果可看出:
a)贮箱充内压状态和无内压状态一阶弯曲模态频率相比,几乎不变。实际模态试验中必须充内压是为了防止贮箱发生壳体失稳,试验和仿真分析航天结构整体模态特性时,可不考虑贮箱内压对其的影响(保证结构不屈服)。
b)对于贮箱的局部壳体呼吸模态,当贮箱内压即使为小量时,充内压状态和无内压状态相比,一阶壳体呼吸频率也是增大较多的。
c)有了结论 a,工程应用中如果研制初期只关心贮箱整体弯曲模态可用梁模型无轴力状态进行分析。
本文相关理论推导是采用梁和平板来类比说明圆筒壳的模态理论的,理想模型验证和实例是采用有限元方法分析的,关于圆筒壳动力学微分方程目前可以给出,但不能给出解析解,只能给出迭代拟合数值解,以后有必要对这方面问题做进一步深入研究,以得出解析解,从而更好的说明内压对圆筒壳结构模态的影响。
