逼近高斯信道容量的M-APSK调制星座优化设计*

蒋炫佑，魏以民，王 雷，彭 磊

(中国人民解放军陆军工程大学 通信工程学院，江苏 南京 210000)

0 引言

当前，为了满足与日俱增的通信用户数量并达到用户不断提高的通信质量要求，通信技术飞速发展。5G标准的实用化指日可待，为适应其109bit/s以上的通信速度要求，不难想象接下来高阶调制将逐渐成为主流的调制方式。而当下众多的调制方式中，较为新颖的幅度和相移键控(APSK)调制与传统调制方案中应用最为广泛的正交幅度调制(QAM)比较，具有更低的峰均功率比(PAPR)和更突出的频谱效率，因此被认为是适应于非线性信道的高效鲁棒传输方案[1-3]。迄今为止，该调制方式已经在标准卫星通信系统中加以采用，如第二代卫星数字视频广播(DVB-S2)等，但由于其相对较差的误码率(BER)性能，在移动通信和地面广播系统中仍很少考虑APSK[4]。

与此同时，结合信息论观点，考虑在功率约束加性高斯白噪声(AWGN)信道传输，如何逼近高斯信道容量仍然是一个具有挑战性的问题[5]。由于在实际中，有限的信号星座点数量必然会导致信号偏离最优连续输入分布，使得绝大多数调制方式的星座容量距离高斯信道容量都有一定差距，因此提出了结合等概率信令与星座整形的有效方法[6-7]。

传统意义上，为AWGN信道设计信号星座分布的原则是在平均功率约束条件下最大化信号星座点间的最小欧几里德距离，以此来改善相应调制方式的误码率指标。在一维信号平面中，基于该原则所采用的服从于均匀分布的信号集能够实现最佳误码率性能，但是，倘若信号集中的点等概率，则又不能满足高斯信道容量可实现的设计前提[3]。因此，在二维信号平面上满足高斯信道容量可实现的APSK星座设计吸引了广泛学者的注意。如对于等概率均匀分布的一维信号，文献[3]中提出了能够逼近高斯信道容量的星座构建方案；而在文献[4]中提出了一种特殊的具有灰度映射的APSK星座，具有较大的整形增益。

值得关注的是，近年来MERIC H提出了一种利用Box-Muller变换[8]构建具有等概率输入信号的APSK星座方案，给出了其在星座点的数量达到无穷大时，可以在二维信号平面上渐近实现高斯信道容量的数学证明，通过仿真验证了其在DVB-S2X系统中具有良好的兼容性[9-10]。但由于该方案未考虑误码率性能，所构建的APSK调制与传统矩形QAM之间存在很大的信噪比差距。

针对以上研究背景，本文提出了一种新的APSK星座构造方案，在满足高斯信道容量可实现的前提上改善最小欧氏距离指标，统筹兼顾星座容量与误码率性能，对其实际应用做了一定的推广。

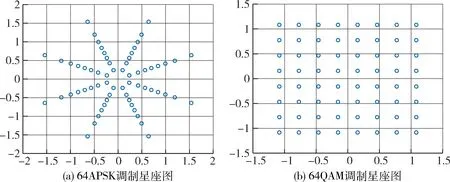
图2 64APSK和64QAM星座分布对比图

1 星座成型过程

本文信号生成过程基于文献中方法，利用Box-Muller变换将服从均匀分布的随机变量转化为服从高斯分布的随机变量。

生成过程可以简单表述为：

首先取0到n-1的整数集合Nn={0,1,2,…,n-1}，基于如式(1)所示离散数集生成信号分布序列：

(1)

然后引入两个在Sn均匀分布的离散随机变量Un和Vn，单独考虑其中每个随机变量的特征函数时，序列(Un)n≥1和(Vn)n≥1都弱收敛于均匀分布(0，1)。

再后定义整形函数φ：(0，1)→R2，根据Box-Muller变换，可得：

(2)

Wn=φ(Un,Vn)=

(3)

其中，P为输入信号的功率限制。

通过上述步骤，产生了均匀分布在R2上的n2对随机向量Wn，星座集Cn呈现出高斯分布，并且均匀分布在n个同心圆上，每个圆上有n个星座点。集合Sn的映射序列确保了Un永不为零，避免了在取对数时出现问题。图1所示是64点APSK调制(n=8且P=1)，由图可知对任意星座点Wn，随机向量Un控制模值，Vn决定相位。

图1 64APSK信号星座图

2 基于增大欧氏距离的优化方案

2.1 优化方向与意义

本小节首先给出同等阶数下APSK调制与矩形QAM调制的星座对比图，如图2所示。

观察分析图2中64APSK与64QAM信号星座分布的对比，可以清楚地看到在最小欧氏距离这一指标上，64APSK并没有传统矩形64QAM星座有优势，这也就意味着在信道参数一致时，第1节所构建的M-APSK调制方式会产生更高的误码率，这项指标的不理想将直接影响到该调制方式的实际应用价值。为此，本节主要研究了基于增大最小欧氏距离的M-APSK调制星座优化方案。

进一步观察，图2中64APSK信号星座在每一条经过原点的直线上星座点都是服从高斯分布的，明显可见在中间圈数上的星座点分布极为密集，因此针对最密集区域对最小欧氏距离做出调整的话，就意味着在整个星座图上做到了优化。基于此本节提出了一种通过旋转重构星座图的整形方法，增大了星座点间最小欧式距离，实现了该M-APSK调制方式在误码率性能上的改善。

2.2 星座优化方案

优化思想：通过对部分星座点的整体旋转，在仍然满足高斯分布的基础上，则可以将原先密集的区域分散到邻近闲置空间上。

根据原始星座图的中心对称性，考虑奇数圈星座点不变，偶数圈星座点旋转角度θ，则θ=π/n，其星座图如图3所示。

图3 偶数圈星座点旋转整形后100APSK星座分布图

可以观察到，此时已经成功将其中央圈数上的星座点再分配开，初步满足了优化目标。对该方案的星座容量性能仿真验证在下一小节中给出讨论。

进一步分析，由于星座图最内一圈的点间距是只与信号的调制阶数有关的，即调制阶数越高分布越密集，当调制阶数取到一定大小时，则此时的星座最小欧氏距离为最内圈点间距。故整形函数的最理想效果即为通过旋转使得最小欧式距离大于等于最内圈点间距。因此，事实上不必像上述优化方案中旋转n/2圈，而是针对几个特定的星座圈进行旋转整形即可达到最佳状态。

由于构建的星座符合圆高斯分布，中央圈数的星座点距离较近，考虑只对第l圈的星座点做旋转整形变换，其中l满足：

l∈{n/2-2,n/2,n/2+2}

那么，同样给出当星座点数量为100时，星座图如图4所示。

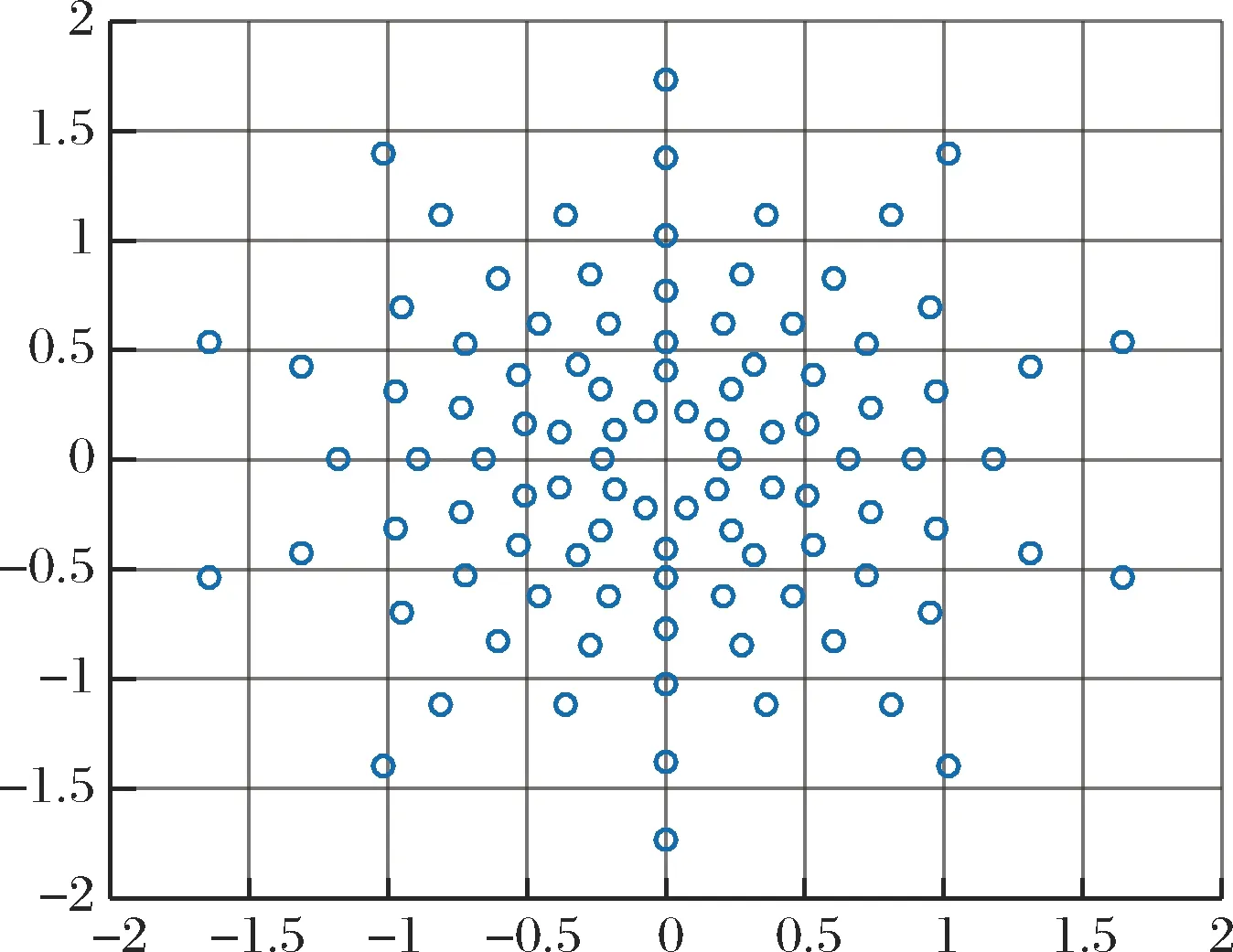
图4 特定圈星座点旋转整形后100APSK星座分布图

2.3 优化方案相关理论推导与证明

2.3.1优化方案性能提升证明

由图3、图4显然可以看出优化方案提升了M-APSK信号星座的最小欧氏距离，首先将优化方案表述为如下过程：对于原APSK信号，针对每条射线边上的点，每奇数顺序的点保持不变，每偶数顺序的点统一(顺时针或者逆时针)旋转角度θ，其中θ为两条相邻射线夹角的一半。

证明：考虑如图5所示，每条射线边的第1、2个点，它们之间的距离代表着最小欧氏距离。如图5所示，星座点变化前有：

d1=R-d3

对于变化后的星座点，根据三角形边的关系公式，有：

d2>R-d3

可得：

d2>d1

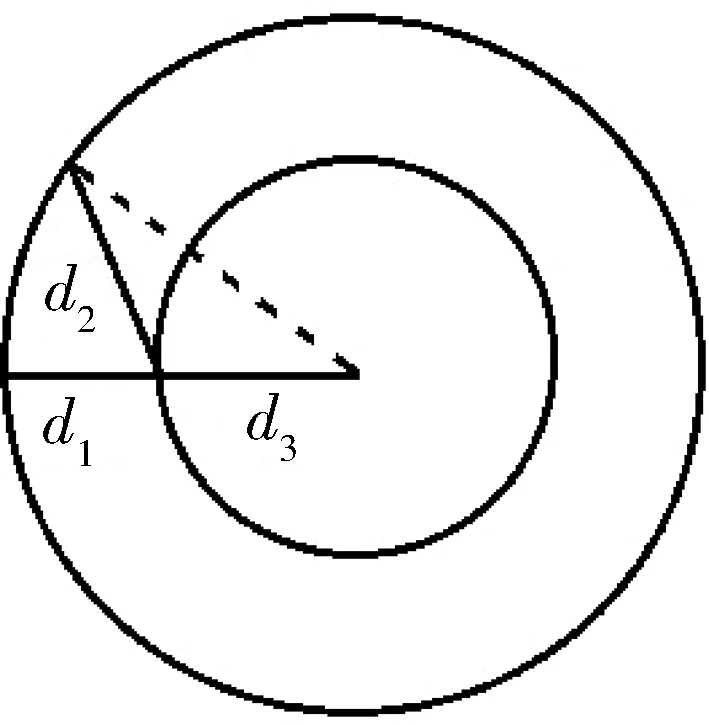
图5 证明图示

那么由最小欧氏距离增大，显然可以得出误码率性能有改善。

该处证明方法多样，可通过解析几何方法先求距离最近的星座点的坐标，再求两点间距离进行比较验证。该方法易于理解但计算过程相对繁琐，在此不做赘述。

2.3.2优化方案满足前置条件证明

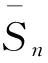
出于严谨性考虑，本小节对优化后方案满足原星座图构建方案前置定理做出补充证明。为便于证明，针对更具普遍性的方案一序列进行，因为方案二是方案一的简化形式，若方案一满足条件，则方案二也必然成立。

参考文献[9]中给出了通过Box-Muller变换构建服从高斯分布输入信号在星座点数趋于无穷大时能够逼近高斯信道容量的两个前置条件：

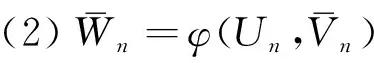
根据第1节得出的结论：构建星座图序列映射中Un控制变换后信号点的幅度，Vn影响角度，则经过整形函数后的优化方案映射序列可以表示成如下形式：

(4)

(5)

其中k越小，对应的点在越外圈的圆上，而序列中每一个元素的值仍在0～1之间。

证明如下：

根据前文分析，改进后APSK在映射关系上只改变了偶数点的Vn，相当于偶数点在同一个圆周上进行角度位移，对应的幅度不变，所以并不会影响模值，即：

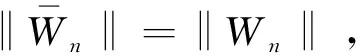
该证明分为以下3个步骤：

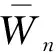
(6)

其中，

将式(4)和式(5)带入式(6)，可得：

(7)

(8)

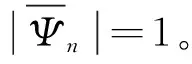
可以得到：

(9)

其中，ΦW*(t)是高斯变量W*的特征函数。

(10)

联立式(7)、(9)、(10)可得：

3 优化方案仿真验证与分析

3.1 两优化方案容量差比较分析

在本小节中，给出M-APSK两次优化方案以及与M-QAM调制方式的比较仿真，以信道容量差作为评价指标，取信噪比SNR为20 dB，则有仿真图6和7。可以得到如下结论：

(1)两优化方案在性能上没有明显区别，由此可见，优化方案二基本保留了优化方案一的性能优势，并且在调制过程中有相当程度的简化；

(2)对比参考文献，优化方案不仅保留了原调制方案在星座点数量多时互信息量接近高斯信道容量的优势，还能在星座点数量较少时保持等同于M-QAM的星座容量，这大大提高了M-APSK调制方式的应用范围与价值；

(3)比较APSK与优化APSK曲线，可以明显看出优化方案的收敛速度超过了原方案。

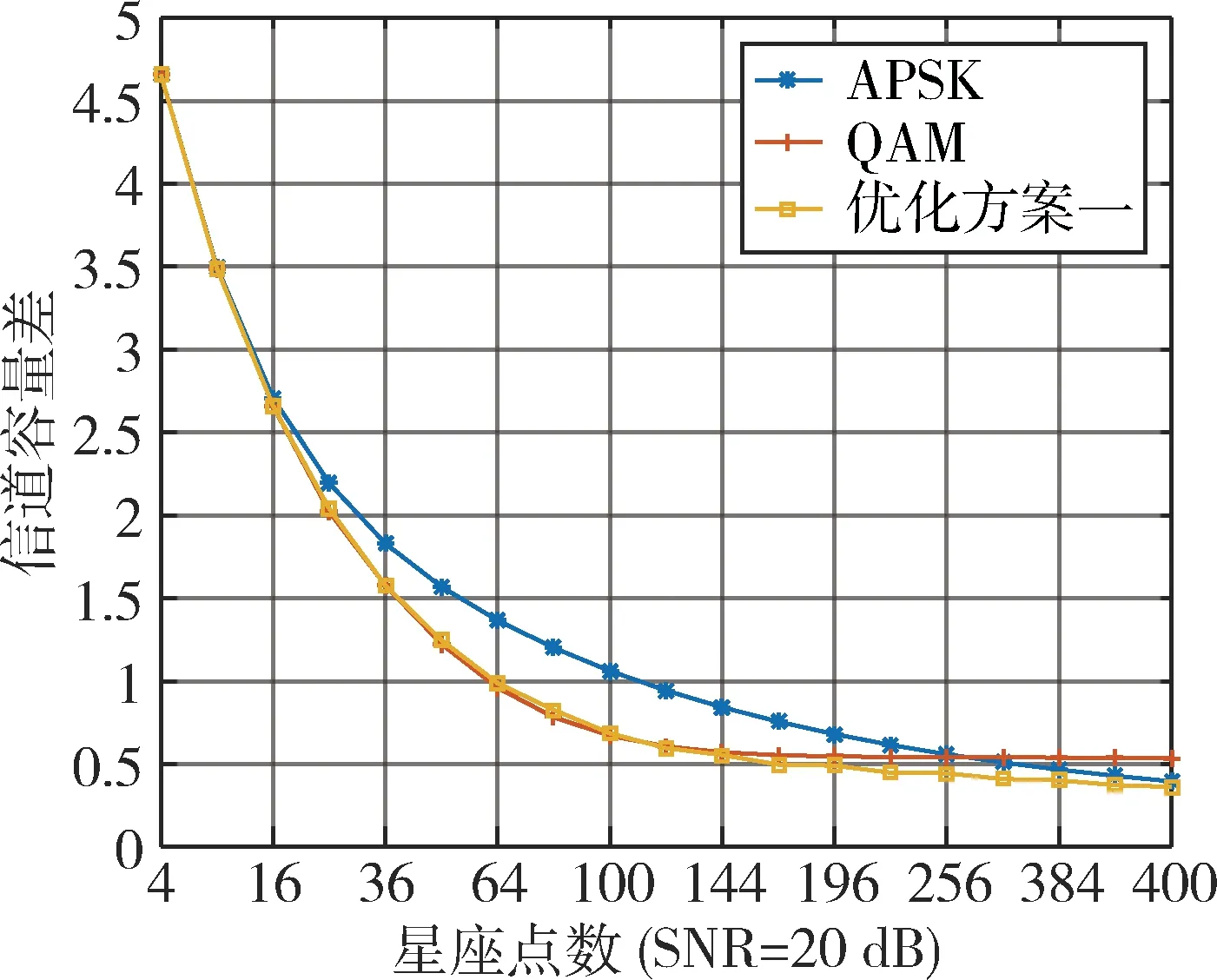
图6 优化方案一与QAM的容量差随星座点数变化示意图

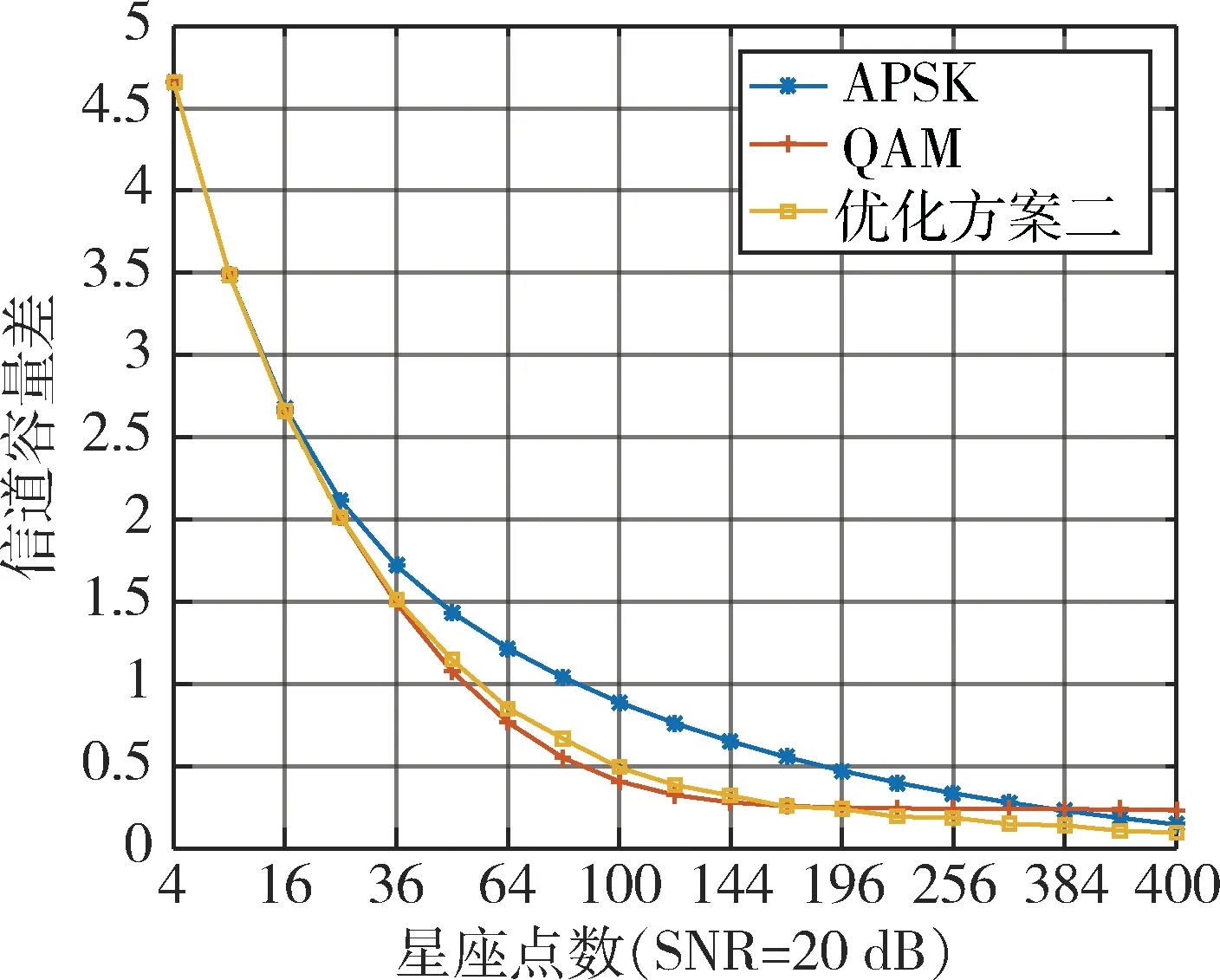
图7 优化方案二与QAM的容量差随星座点数变化示意图

保留优化方案二，给出4APSK、16APSK、64APSK、4 Modified APSK、16 Modified APSK以及64 Modified APSK 6种调制方式的星座容量随信噪比变化，如图8所示。

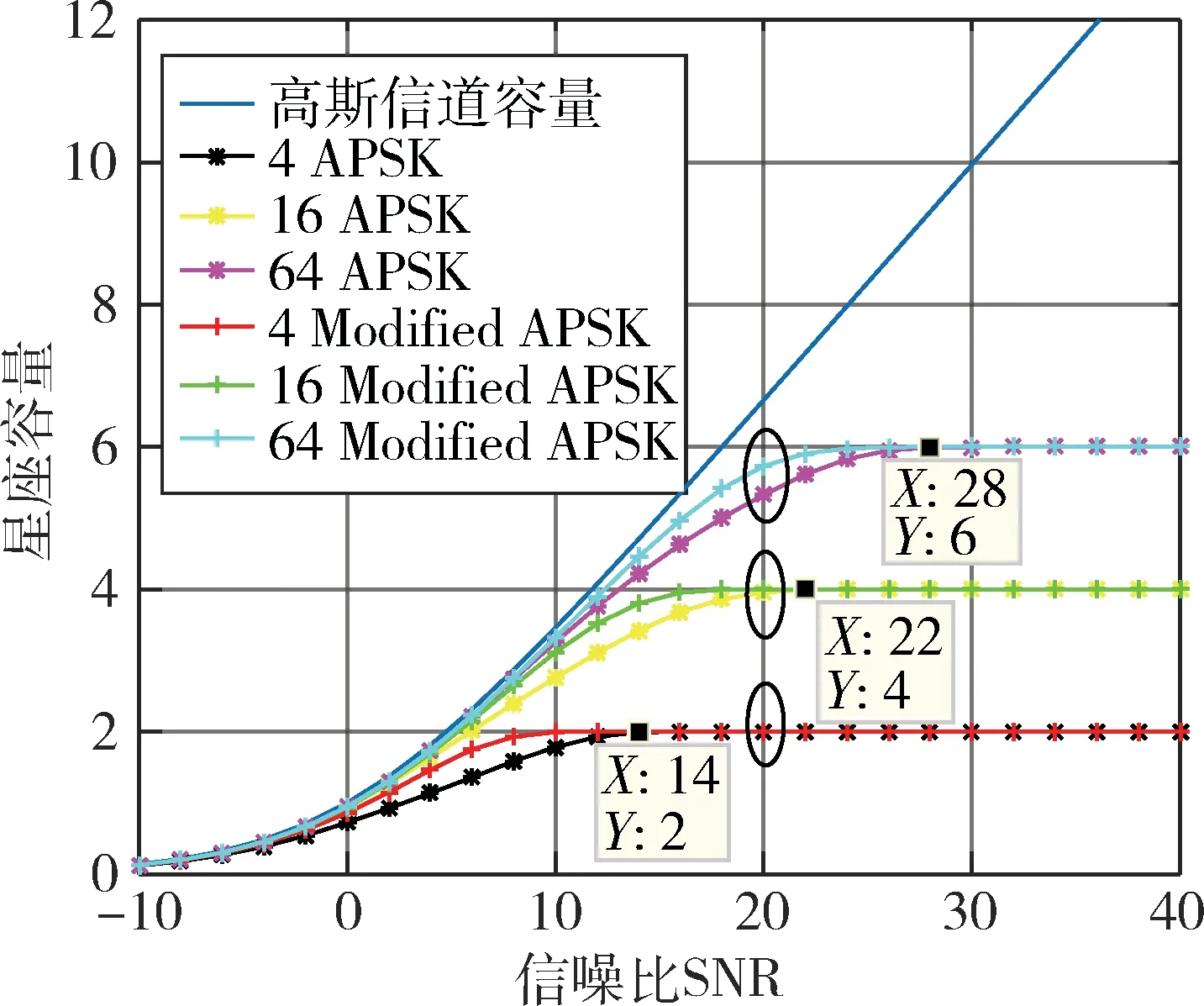
图8 多种调制方式的星座容量随信噪比变化示意图

3.2 两优化方案误比特率比较分析

如图9所示，Modified APSK为优化方案二的误码率曲线，经比较可得出结论：旋转整形后的星座分布，有效地增大了最小欧氏距离，在误码率指标上取得了明显改善。

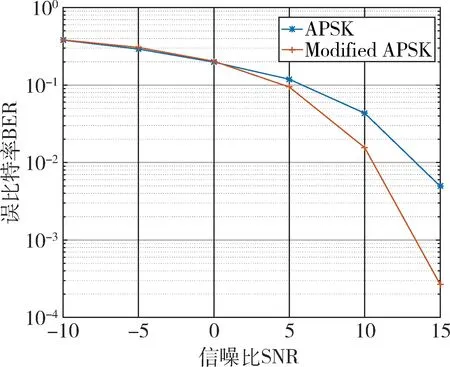
图9 优化方案与原方案误比特率对比图

综合星座容量与误码率仿真分析结果，优化方案较原始方案均表现出一定的性能优势，并且优化方案二相比方案一大大减少了系统复杂度，降低了对收发两端的性能要求，因此可以说优化方案二已经基本达到了本文的优化目标。

4 结论

本文提出了一种新的整形函数来优化已有的性能较好的APSK星座分布，基于高斯信道容量可实现的APSK星座构造目标，通过联合考虑最大可实现率和最小欧氏距离构建出了性能更好的星座分布。通过综合性能仿真结果验证了所提方案在误码率和容量性能方面的优势。对于给定调制阶数的信号星座，本研究认为在略微放松信号分布条件时，在APSK星座的设计中将获得更快的收敛速度。