基于降维的人脸识别方法研究与应用*

简彩仁，庄凌宇，林智鹏

(厦门大学嘉庚学院,福建 漳州 363105)

0 引言

人脸识别是基于人脸的面部特征辨识身份的生物识别技术。人脸识别最主要的用途是确定人的身份。随着计算机技术的不断发展，人们获取人脸图像数据变得异常容易，因此人脸识别的发展和应用更是不断深入和普及。人脸识别技术已经广泛应用在军队、医疗、银行、公安、电子商务等行业。由于当前人脸识别的应用场景得到的高维数据愈发庞大，因此研究基于降维的人脸识别方法具有重要的意义。

人脸识别研究是当前研究的热点问题。许多降维方法被应用于人脸识别研究。基于线性降维方法的人脸识别研究代表性方法是线性判别分析(LDA)[1]，该方法使降维数据类内距离小，类间距离大，但是对小样本数据容易产生非奇异解。基于流形学习的降维方法，如等距映射(ISOMAP)[2]、局部线性嵌入(LLE)[3]等，旨在保持局部结构实现降维，更适合非线性数据的降维，但是这些方法严重依赖于近邻关系，当存在较小误差时，可能会对全局估计产生较大的影响。基于稀疏表示的降维方法在人脸识别中也有重要的应用，该方法的优点是可以避免过拟合问题，但是运算效率不高[4-5]。

本文从降维的角度研究人脸识别。通过线性降维方法主成分分析和非线性降维方法核主成分分析对人脸图像数据进行降维研究。降维方法可以有效剔除人脸图像数据的冗余特征，从而提高识别准确率。通过实验比较降维人脸图像数据与原始人脸图像数据的识别准确率。

1 相关方法

1.1 主成分分析

主成分分析(Principal Component Analysis，PCA)方法将一组可能存在相关性的变量通过正交变换转换为一组线性不相关的变量，使其成为统计的依据，转换后的这组变量叫主成分。主成分分析的主要思想是投影样本点的方差最大化。从最大可分性的角度可以对主成分分析进行另一种解释。通过投影矩阵W将样本点xi投影到新空间的超平面上，投影得到WTxi。可以通过最大化投影样本点的方差达到尽可能区分投影样本点的目的。

s.t.WTW=I

(1)

通过拉格朗日乘子法，式(1)可以通过特征值问题XXTW=λW求解。

1.2 核主成分分析

主成分分析是一种经典的线性降维方法，但不利于发现高维小样本数据的本质特征。针对这一不足，核主成分分析基于核理论对主成分分析进行“核化”，扩展成适合非线性降维的方法。

给定非线性特征空间映射Φ:Rm→M，其中Rm为高维样本空间，M是低维流形空间，因此原始高维数据X的低维流形表示为Φ(X)。对高维空间样本Φ(X)进行主成分分析得到核主成分分析问题的优化目标函数为：

s.t.WTW=I

(2)

直接定义非线性映射Φ(X)是困难的，核表示理论给出了一种不需要定义非线性映射的技术[6-7]。设K∈Rn×n是一个半正定核矩阵，它们的元素定义为:

[K]ij=[(Φ(X),Φ(X))M]ij=Φ(xi)TΦ(xj)=k(xi,xj)

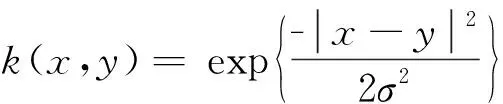
因此核主成分分析的目标函数(2)可以转化为:

s.t.WTW=I

(3)

通过拉格朗日乘子法，式(3)可以通过特征值问题KW=λW求解。

2 基于降维的人脸识别方法

人脸图像数据具有高维数的特点，因此人脸图像数据存在大量的冗余，通过降维可以得到更适合人脸识别的数据集。本节利用主成分分析和核主成分分析研究基于降维的人脸识别方法。

首先利用主成分分析或核主成分分析对数据集进行降维，再对降维后的数据集进行识别研究。结合第1节的理论，将基于降维的人脸识别方法的实现步骤总结成如下算法：

算法:基于降维的人脸识别方法输入:人脸图像数据集X,主成分保留比率pcaratio输出:识别准确率acc(1)标准化训练人脸图像数据集X,使每个样本具有单位L2范数;(2)利用式(1)或式(3)求投影矩阵W;(3)对投影数据WTX用K最近邻分类法进行分类。

3 实验分析

本节通过实验验证主成分分析和核主成分分析两种降维方法对人脸识别的影响。

3.1 数据集简介

实验数据集为两个常用的人脸识别数据集Yale和ORL。

Yale人脸数据集总共采集了15个人的人脸图像，该数据集共15个类别，165个样本，特征数量为1 024个。在这15个对象中，每一个对象都具有11张各不相同的人脸。在这些图像中，包含各种阻挡因素，例如角度因素、光照强度因素、相关环境变化因素以及遮挡物的影响和不同表情的变化等。图1为部分Yale人脸图像。

图1 Yale人脸图像示意图

ORL人脸数据集共有40个对象，每一个对象都具有10张人脸，总数量达到400张灰度图像人脸，特征数量为1 024个。每一个对象的人脸通过观察存在肉眼可见的变化，包括遮挡物的变化、表情的变化等，在此基础之上每个人脸的每一张图片的大小都是按照一定的规律进行渐次变化，并且每个人脸之间存在20°的水平以及垂直的旋转变化。图2为部分ORL人脸图像。

图2 ORL人脸数据示意图

3.2 实验参数设置

实验环境为Windows 7系统，安装内存8.00 GB(3.42 GB可用)，用MATLAB R2011b编程实现。利用交叉验证对比各种方法下的识别准确率。对两个数据集通过主成分分析(PCA)和核主成分分析(KPCA)进行降维后与原始数据集进行对比，选用K最近邻分类法进行分类对比分类准确率和运行时间。实验参数设置如下：主成分保留比率为90%，K最近邻分类法的最近邻参数选为1，交叉验证折数设置为{4,5,6,7,8,9,10}。比较方法为原始数据用K最近邻分类(KNN)、主成分分析降维数据用K最近邻分类(PCA-KNN)、核主成分分析降维数据用K最近邻分类(KPCA-KNN)。

3.3 实验结果与分析

实验1：Yale人脸图像数据集识别实验。该实验利用KNN、PCA-KNN、KPCA-KNN 3种方法研究Yale人脸图像数据集的识别准确率。在不同交叉验证折数下的识别准确率如表1所示，图3也直观显示了不同方法的识别准确率。

表1 Yale人脸图像数据识别准确率对比 (%)

图3 Yale人脸图像数据集识别准确率对比图

从表1和图3的实验结果可以发现，降维后的数据集具有更好的识别准确率。因此降维方法可以有效地缓解人脸图像数据的冗余问题。再对比核主成分分析和主成分分析两种降维方法，发现KPCA-KNN方法显著优于PCA-KNN，这反映了核主成分分析这种非线性降维方法更适应人脸图像的非线性性质，从而取得更好的识别准确率。

此外，表2给出了不同方法对Yale人脸图像数据集进行识别的运行时间。

表2 Yale人脸图像数据集识别时间对比 (s)

从表2可以发现，降维后可以明显提高识别的效率。而且，非线性降维方法KPCA比线性降维方法PCA更有效率。

实验2：ORL人脸图像数据集识别实验。该实验利用KNN、PCA-KNN、KPCA-KNN 3种方法研究ORL人脸图像数据集的识别准确率。在不同交叉验证折数下的识别准确率如表3所示，图4直观显示了不同方法的识别准确率。

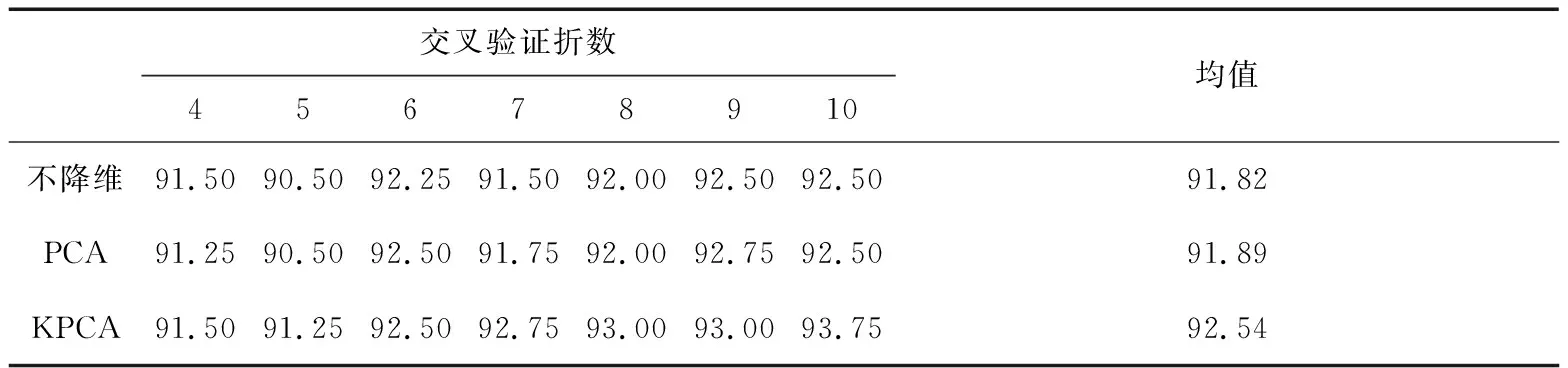
表3 ORL人脸图像数据识别准确率对比 (%)

图4 ORL人脸图像数据集识别准确率对比图

从表3和图4的实验结果可以发现，ORL人脸图像数据集的识别实验结果与Yale人脸图像数据集的识别实验结果类似：降维有利于人脸图像的识别，并且核主成分分析这种非线性降维方法更适应人脸图像的非线性性质，有更好的识别准确率。

表4给出了ORL人脸图像数据集在不同交叉折数下进行识别的运行时间。

表4 ORL人脸图像数据集识别时间对比 (s)

从表4的运行时间对比可以发现，降维可以明显提高识别的效率。非线性降维方法KPCA比线性降维方法PCA更有效率。不仅如此，当样本的个数更多时，KPCA的运行效率比PCA有明显的改善。

通过以上两个人脸图像识别实验的识别准确率和运行时间对比分析，可以明显地发现经过主成分分析和核主成分分析的降维，无论是识别准确率还是识别效率对比无降维数据，都具有显而易见的优势。其中，核主成分分析作为主成分分析的改进，比主成分分析有更加精确的识别准确率以及更好的识别效率。

4 结论

本文利用主成分分析和核主成分分析对基于降维的人脸识别方法进行了研究。实验结果表明降维可以有效地提高人脸识别准确率，而非线性降维方法更适合人脸图像数据的降维。不仅如此，降维后的数据可以明显提高识别效率。因此，本文的研究具有一定的实用价值。