基于核心素养下的数学审题能力和习惯培养

李学成

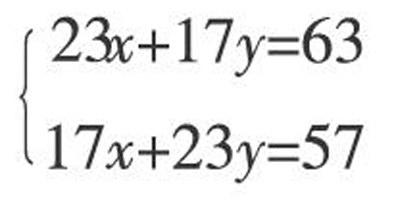
【摘要】  审题贯穿于学生整个数学学习过程，是一个不断收集数据、挖掘数据、处理数据各处理数据过程，据此，教师要坚持一切从学生中来，再到学生中去的原则，坚持为学生提供展示及合作交流的空间与时间，体现“一切为了人的发展”的教学理念，以现有的资源，培养学生认真细致的好习惯，增强学生批判精神和探究兴趣，推动学生自主学习和实践创新，让核心素養接地气。

【关键词】  审题 收集数据 挖掘数据 处理数据

【中图分类号】  G633.6 【文献标识码】  A 文章编号】  1992-7711（2018）09-001-02

审题是合理、正确解题的基础，是获取解题信息，探寻从条件通往结论之路的过程，是一个多种思维与策略参与的、非常曲折的过程，是一个贯穿于学生整个学习过程。审题能力与核心素养互为表里，审题能力强，则核心素养厚，核心素养厚，则审题能力强，审题能力与习惯的关系也是这样。解题的过程不过是把从条件通往结论之路“走”一遍，非常遗憾的是，受应试教育的深刻影响，大部分学生接收信息都是海绵式的，这样接收的信息大多不经过思考，囫囵吞枣，而后遗忘，对人的益处少之又少。

数学考试成绩出来了，经常有学生感叹：“怎么这个题目做错了”，“我都会的，就是马虎了”。听到这样的话，教师放心了，家长也放心了，叮嘱一下以后不要粗心好像问题解决了。事实上本质不是粗心，而是能力问题，是学生各种审题能力存在缺陷具体表现，而学生审题能力存在缺陷的根本原因，是我们在解题训练中少有让学生经历审题的曲折过程，教师的包办代替，潜移默化中让学生失去了思考的积极性，养成“懒惰”习惯，“懒惰”下哪有能力？这是导致学生核心素养不足的根本原因。

各科学习本质上是数据采集、数据挖掘和数据处理过程，数据采集、数据挖掘和数据处理是最基本的学习素养，数学学习尤其这样，数学中的审题基本上含盖了数据收集、数据挖掘和数据处理。由于学生生活经验不同，知识储备不同，看问题视角不同，对数据收集和挖掘一定存在不同，对这些发散数据的处理，有的能使问题获得解决，有的则不能，教师要有耐心，学会等侍，让学生充分表达，让一些“想不到”出现，让正确与错误碰撞，只有这样才能让学生充分经历审题的曲折，良好的审题习惯和能力在这一过程习得，试图通过几次讲座不可能习得审题习惯和能力。

当前，以互联网、大数据、人工智能为代表的新一代信息技术日新月异，给各国经济社会发展、国家管理、社会治理、人民生活带来重大而深远的影响，增强学生数据收集、数据挖掘和数据处理能力，会使他们更好地适应将来的生存与发展，这正是提出《中国学生核心素养》的初衷。

收集数据培养认真细致的好习惯

读题是培养审题能力的第一步，它的重要目的是从问题情境中收集数据，特别是那些隐含的数据。是否读懂题意，就是看他收集的数据是否准确、全面，这不仅是而后合理正确解题的需要，更让学生明白收集数据是审题的出发点。所谓的习惯养成，就是你明白什么事该么怎样做，并坚持做下去，最终养成习惯。我们经常发现，很多学生在解决问题时经常会用眼睛扫一遍，就急于动笔了，因为他们觉得这是司空见惯的问题，而事实上题目并不是他们“经验”里的样子，题目的意思已经发生改变，如果没有发现这些改变而使用原来的套路，一定会使解题陷入困境。

例1解方程组

这是一道普通的二元一次方程组解答题，受思维定势负迁移影响，学生会很轻易选择常用的代入消元法或加减消元法求解，然而，由于未知系数较大，导致解题过程很繁，绝大部分学生难于得到正确答案，甚至丧失解题信心。其原因是收集数据时，忽略了“方程组中相同未知数的系数和”相等这一隐含数据收集与应用。如何处理这一对数据，教师不要包办代替，要鼓励学生大胆想一想，学生敢想、爱想、善想是审题又一好习惯。把方程组中两个方程左右两边相加，就能得到40x+40y=120，进一步处理得到x=3-y，这样解题才回到解二元一次方程组求解的常规套路。

学生陷入解题困境是常有的事，教师不应急于告诉学生解题方法，而应鼓励学生再次审时度势，回望问题，看看有没有遗漏掉的数据。其实这是一个发现的过程，突破思维定势创新的过程，很难，它要求和别人看相同的事物却能得到不同的结论，然而，避开这些“难”的挑战，就不会有审题能力的提高。

挖掘数据培养批判精神和探究兴趣

收集完情境数据，找到“解题之路”的起点，教师应引导学生挖掘数据，再进一步，看看这些收集到的数据背后隐含的数据是什么。这时需要改变分析思路，变动观察视角，从直观眼前的文本洞察收集数据背后的世界，深入到解决问题的本质，寻求到一条最适合的解题之路。

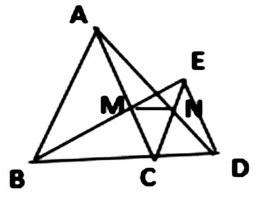
例2如图， ⊿ABC和⊿ ECD都是等边三角形，且B、C、D三点在同一直线上，BE、AC相交于M，AD、CE相交于N.求证：BE=AD.

通过读题，可收集到数据“ ⊿ABC和⊿ECD都是等边三角形，且B、C、D三点在同一直线上”，简单挖掘可以得到数据“AB=BC=AC，CE=CD=DE，及⊿ABC和 ⊿ECD各内角等于60°，∠BCD=180°，等边三角形⊿ABC和⊿ECD各边上的高、中线、对角平分线重合”.为使挖掘深入进行下去，这时应该鼓励学生想一想：线段AB、BC、AC、CE、CD、DE还是哪些三角形的边，哪些三角形包含线段BE、AD，再次引导学生有目的观察图形，深入图形，挖出数据：AB是⊿ABD的边，AC是⊿ACD的边，BC是⊿BCE的边，CE是⊿BCE的边，CD是⊿ACD的边，DE是⊿BDE的边，AD是⊿ACD和⊿ABD的边，BE是是⊿BDE和⊿BCE的边。让具有特殊关系的线段“动”起来，在批判已有的数据中发现新数据，挖掘的过程不在冰冷、乏味，探究的兴趣就可以显现出来。

通过二次挖掘，得到众多新数据，为问题解决提供了丰富思维材料，进一步追问下去，探究的趣味就更加浓烈，对发展学生核心素养也更有帮助。这时，教师要求学生想一想，证明两条线段相等常见的方法是什么，学生探究就会有支点，比如，二次挖掘的数据中根本就没有含有AD、BE的三角形，也就排除用等腰三角形判定解决问题，学生不断地怀疑和求证就有充分的证据。沙中淘金，在批判旧世界中发现新世界，通过观察比较含有线段AD、BE的三角形，⊿ACD和⊿BCE具有相等的元素更多，隐含条件∠BCE=∠ACD中的角也含在⊿ACD和⊿BCE中，解题之路也就锁定了，解题不再是聪明人的游戏，学生批判精神和探究兴趣就此生成。

处理数据推动自主学习和实践创新

例2问题解决了，如前述，不断调整视角，调整学习方法，学生能够感受学习过程的艰辛和乐趣，深刻体验几何证明中的分析与综合，习得相关知识与技能。但学生探究如果就此止步，就会浪费本例的训练价值。事实上看看人类发展的历史，它就是不断建立超自然存在、超世界存在的历史，人类社会的进步很大程度上也在于此，比如，以前没有汽车后来有汽车了，以前没飞机后来有飞机了。

面对例2解题过程中收集和挖掘到的众多数据，教师应鼓励学生再反思，本例是否只能推出AD=BE？显然不是，由于学生生活经验不同，知识储备不同，看问题视角不同，学生发现的结论不会完全一样。除了问题的原结论外，还有AC∥DE，AB∥CE，MN∥BD等不下二十结论，这样在不经意间做了二十多个题，其效率与效益是“题海”战术无法比拟的。

为鼓励学生能够持续的研究问题，想得更深入一点，学得更清晰一点，能够把学的知识、方法，在一个新的领域应用，鼓励学生反过来想一想，条件“ΔABC和ΔECD都是等边三角形”，在解题中起的作用是什么，这种作用能否被其它特殊三角形代，如等腰直角三角形、一般等腰三角形，条件“B、C、D三点在同一直线上”能否省去。通过这样有机的变式训练，实施对原型题的超越，推动自主学习和实践创新。

审题贯穿于学生整个学习过程，只要教师坚持一切从学生中来，再到学生中去的理念;坚持为学生提供展示及合作交流的空间与时间，在此过程中注重学生收集数据、挖掘数据、处理数据的能力培养，学生审题能力一定能够提高，审题的好习惯就能养成。

[ 参  考  文  献 ]

[1]教育部.中国学生发展核心素养（征求意见稿）.

[2]周莺.语文学科如何发展学生核心素养湖北教育，2017（2）11-12.